FSM Machine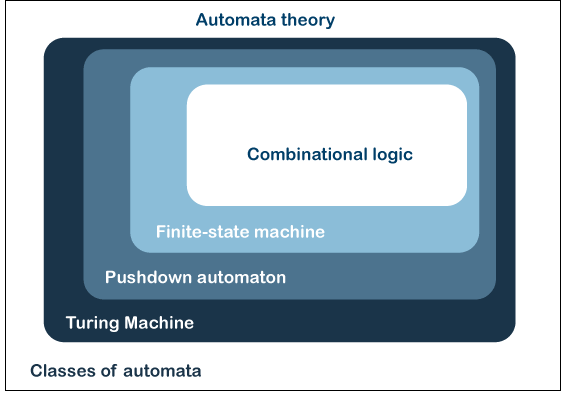

A finite-state machine (FSM), sometimes known as a finite automaton ((FSA), plural automata, or essentially a genetic algorithm, is a mathematical formula of computing. It's extraction and analysis that can only be one of a restricted number of states at any particular moment. In reaction to a certain stimulus, the FSM can shift from one form to another; this shift is referred to as a shift. An FSM is represented in the form of modes, a starting state, and the stimuli that cause each shift. There are two kinds of finite-state machines: deterministic finite-state machines (DFSM) and non-deterministic finite-state machines (NDFSM). A deterministic finite-state machine can be built in the same way as a non-deterministic one. The activity of state machines may be noticed in several smart technologies that conduct a planned set of activities consisting of a sequence of events provided to them. Convenience stores, which distribute brands when the correct combination of tokens is collected, stairwells, whose pattern of halts is dictated by the ceilings received by riders, stop signs, which modify series when cars are getting ready, and tandem latches, which necessitate the information of a series of symbols in the right order, are simple instances.

The finite-state machine has very little processing capability than other numerical simulations, including the Turing computer. Because of the computational resource's differential, there are some computational jobs that a Quantum computer can perform but an FSM (Finite-state machine) cannot. This is due to the fact that the number of phases in an FSM limits its capacity.

An instance: A coin-operated barrier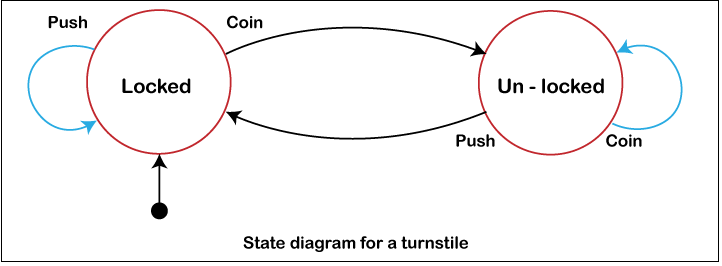

A turnstile is an instance of a basic operation that may be expressed by a state machine. A barrier is a barrier with three rotating limbs at waist level, one around the doorway, used to regulate admission to subway systems and theme park attractions. Originally, the limbs are closed, obstructing the entrance and prohibiting customers from moving in. By inserting a coin or token into a hole on the turnstile, the arms are unlocked, enabling a solitary consumer to pass over. Once the consumer has passed through, the arms remain locked for another coin to be placed.

The turnstile, when seen as a state machine, has 2 conceivable phases: Locked phase and Unlocked phase. There are two parameters that can change its situation: inserting a coin into the frame (coin) and attempting to push the arm (push). Attempting to push on the arm has no influence on the lock position. There is no matter how many people the interface push is granted, as it always remains in the lock position. Inserting a coin means providing the system with a coin input that changes the state from Restricted to Unlocked. Conversely, a consumer pushing via the arms and providing a push stimulus returns the status to Locked.

The turnstile neural network may be described by a state-transition table, which shows the transformation across each conceivable state (depending on the input supplied to the machine) and the outcomes that come from each input: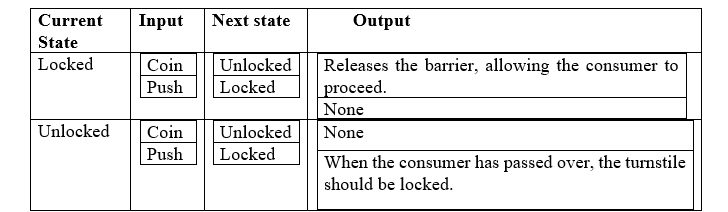

A basic method, which is a unit vector, may also be used to depict the transversal state machine. An edge maintains each phase (circle). Moves from one phase to another are represented by vertices (arrows). The stimulus that causes the shift is indicated on each line. A round arrow reverting to the original condition represents an intake that does not produce a change in circumstances (including a coin entered in the Unlocked condition). The black dot's movement into the Locked component signifies that it is at its start point.

Terms and Notions

A state is a representation of a platform's current situation as it awaits the execution of a shift. A shift is a sequence of activities that must be performed when a criterion is fulfilled, or an incident happens. For instance, when listening to the radio on a sound device (the device is in the "radio" phase), obtaining a "next" input causes the device to go to the last channel. When the equipment is in the "CD" mode, the "next" stimulation enables the company to advance to the next record. Multiple behaviors are triggered by comparable inputs based on the present condition.

It is also feasible to correlate operations with states in several finite-state machine depictions:

An entry action is anything that is done when you join a state.

An exit action is one that is carried out upon leaving a state.

Illustrations of FSM

Table of States and Events

There are various forms of state-transition tables. The most typical form is presented below: the conjunction of the present state (e.g., B) and the stimulus (e.g., Y) represents the next state (e.g. C). The entire activity is not explicitly detailed in the chart and must be supplemented with references. Using state charts, you may create an FSM definition that provides all of the act's details.

Table of State-transition

Unified Modelling Language (UML) Machine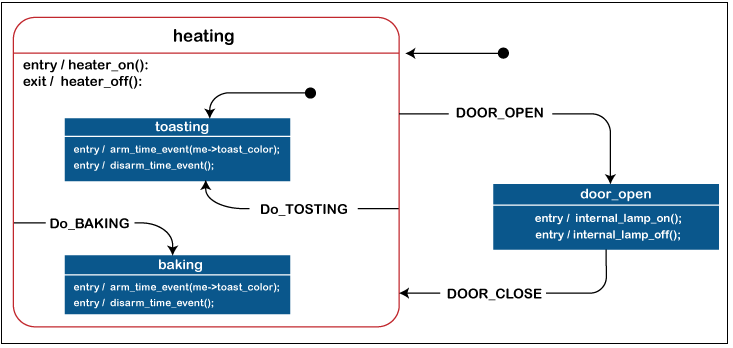

State machines are described using a symbol in the Unified Modeling Language. UML state devices transcend classic finite-state system restrictions while keeping their primary features. UML state networks include new ideas such as hierarchical structures, stacked states and perpendicular zones while also expanding the idea of operations. Unified modelling language state machines exhibit properties of both Goopy and Turing machines. They allow for activities that are dependent on both the platform's configuration and the particularly evident, as in Mealy systems, as well as entry and exit operations that are connected with stages instead of phases, as in Turing machines.

Specification and description language State machine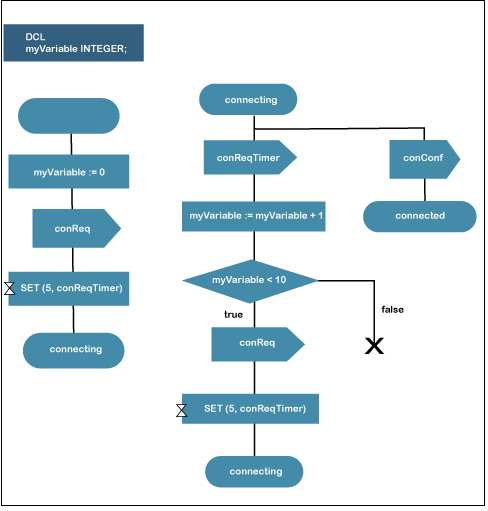

Description and Specification Language is an ITU specification that contains concepts and includes to express transitional acts:

• Send a notification
• Get a notification about an event
• Set a timer
• Pause a timer
• Begin another concurrent state machine
• Final decision

To render the finite-state system operational, SDL integrates fundamental data structures known as "Abstract Data Types," an activity language, and implementation logic.

Simple finite state machine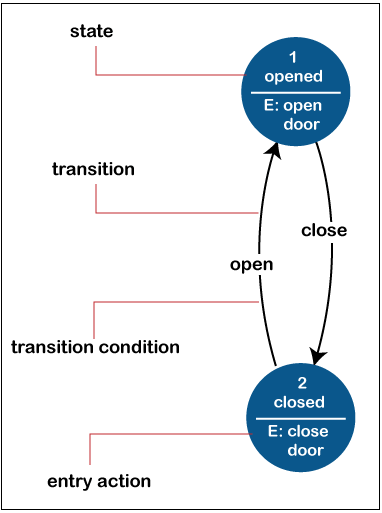

There are several ways to depict an FSM, including the one shown in the above figure.

Usage of FSM

Finite-state systems are important in many fields, such as electrical engineering, languages, software engineering, psychology, physiology, arithmetic, computer game development, and reasoning, in contrast to its usage in simulating responsive networks. Finite-state systems are a type of device investigated in computational geometry and computation theory. Finite-state systems are frequently used in computer engineering for simulating web applications, designing equipment, digital equipment, software development, translators, security mechanisms, and the research of computation and linguistics.

Types of FSM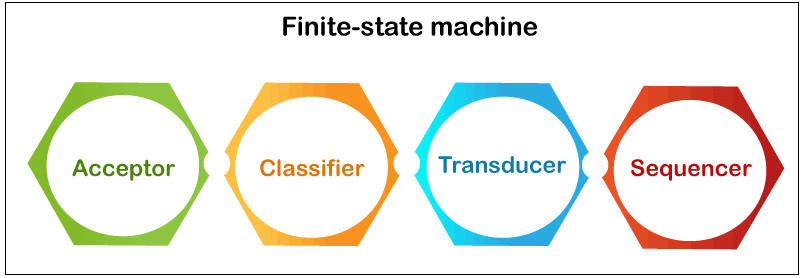

Acceptor, transducer, classifiers, and sequencers are all types of finite-state systems.

• Acceptor

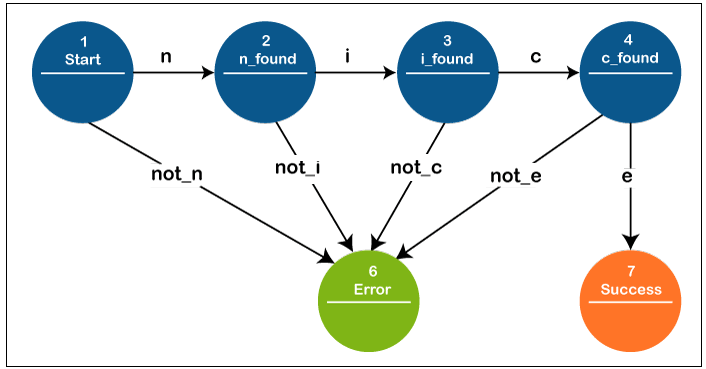
Acceptors (also known as recognizers or detectors) generate a binary number that indicates not if the incoming input is acknowledged. An acceptor's condition is either receiving or non-accepting. Once all information has been obtained, the input is acknowledged if the present state is receptive; alternatively, it is denied. In most cases, input is a string of signs (characters); no interventions are required. The acceptor takes the infinite loop if the beginning state is also an adopting condition. The figure demonstrates an acceptor that takes the string "lovely." The single accepted phase in this acceptor is phase 7.

A presentation is a (potentially infinite) collection of sign series that is a regular dialect whether there is some acceptor that receives that set. The collection of character variables with an even sequence of 0, for instance, is a regular language (as shown in the figure), although the group of all strings are "not" whose duration is a large integer.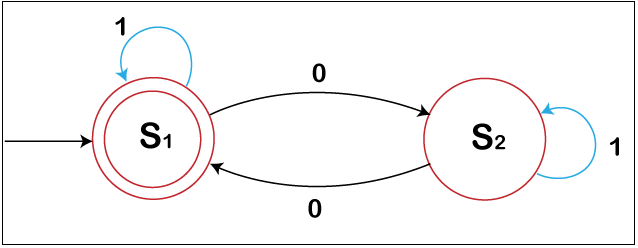

An acceptor may alternatively be defined as specifying a dialect that contains all strings approved by the purchaser but none of the refused ones; that language is recognized by the acceptor. The languages acknowledged by acceptors are regular languages.

The figure shows an instance of an accepted phase: a deterministic finite automaton (DFA) that determines if the binary representation string has an even sequence of 0s.

S1 (also known as the initial position) denotes the state in which an even sequence of 0s has been entered. As a result, S1 is an acceptable state. If the binary series contains an even sequence of 0s, this acceptor will complete in an approved phase (involving any binary string containing no 0s). This acceptor accepts strings such as ? (the integer value), 1, 11, 11..., 00, 010, 1010, 10110, and so on.

• Classifier

Classifiers are a subset of inclusions that provide an n-ary response when n is bigger than two.

• Transducer

Transducers use actions to generate output associated with given input and/or state. They are employed in process control as well as in natural language processing.

There are two sorts of system control applications:

Moore machine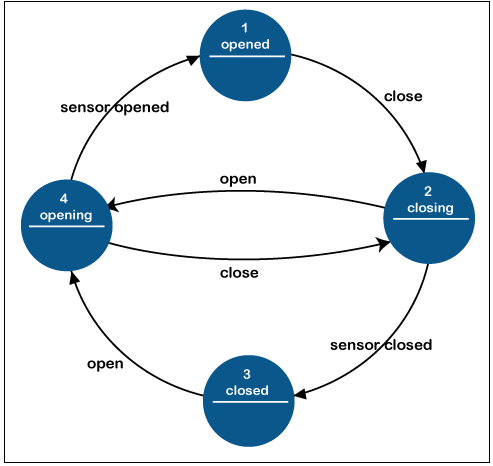

The FSM only employs entry events. Hence the output is only determined by the state. The Moore method has the advantage of simplifying behavior. Take a look at an automatic door. The state machine identifies two instructions that cause transformations: "command _open" and "command_close." The entrance activity (E:) in phase "Opening" begins a motor that opens the door, whereas the entrance activity (E:) in stage "Closing" begins a motor that closes the door. When the motor is fully opened and closed, the phases "Opened" and "Closed" terminate it. They communicate the status to the outside environment (for example, to other physical systems): "door is wide open" or "door is locked."

Mealy machine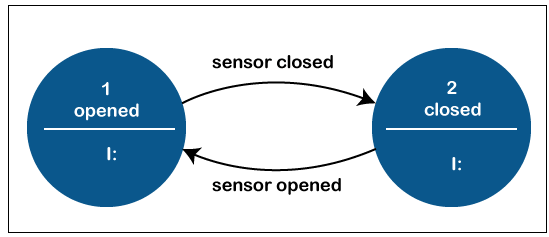

The FSM also employs input operations, which means that output is dependent on input and status. The implementation of a Mealy FSM frequently results in a decrease in the number of countries. Figure 7 depicts a Mealy FSM providing the similar behavior as in the Moore instance (the behavior depends on the implemented FSM execution model and will work, e.g., for virtual FSM but not for event-driven FSM). There are two input activities (I:): "begin motor to shut the door if command close comes" and "begin motor to unlock the door if command open enters." The transitional stages "opening" and "closing" are not depicted.

• Sequencer

Sequencers (also known as generators) are a type of receiver and converter with a single output language. They only create one series, which may be seen as a receiver or converter output vector.

Determination

There are also non-deterministic (NFA, GNFA) and deterministic (DFA) automata. Every phase in a deterministic algorithm has precisely one movement for each conceivable intake. An intake in a non-deterministic algorithm might result in one, upwards of one, or no shift for a particular state. Any non-deterministic automata may be transformed into a (typically more complicated) deterministic automaton with equivalent capabilities using the datatype building procedure.

A "combinational FSM" is a finite-state machine (FSM) with only one phase. It only permits operations while entering a state. This approach is beneficial when a lot of finite-state systems must collaborate, and it is advantageous to view a completely algorithmic portion as a type of FSM to fit the functional prototypes.

Differential semantics

Other ranges of definitions can be used to characterize state machines. There are methods for analyzing and creating algorithms for sensory integration. They integrate multilevel modules (which often have more than one present state), flowing charts, and truth tables into a particular language, culminating in a unique syntax and range of interpretations. As Harel's initial state systems, these truth tables enable hierarchical stacked phases, orthogonal areas, state policies, and transitional decisions.

Implementations of FSM

Software applications

The following parameters are frequently used in the development of software programs using finite-state devices:

• Programming with automata.
• Finite-state machine triggered by events
• A simulated finite-state machine is a device that has a finite number.
• Declare the model structure.

Hardware application

An FSM may be implemented in a communication system utilizing an embedded software gadget, programmable logic, logical operations, and flip flops or switches. A developed system, in particular, necessitates the use of registers to hold system states, a piece of combinational circuits to decide the data structure, and a secondary unit of combinational circuits to decide the outcome of an FSM. The Richards regulator is a traditional hardware implementation.

The result of a Medvedev machine is clearly attached to the phase switch, reducing the lag time among the flip-flops and the outputs.

Reduced power computer programs can be improved for energy consumption via phase coding.

Compiler and FSM

In the interface of scripting language processors, finite automata are frequently utilized. A frontend like this may be made up of numerous finite-state systems that perform a lexical analyzer and a decoder. The lexical analyzer constructs a series of linguistic symbols (like special characters, strings, and symbols) from a series of letters, from which the processor constructs a syntactic structure. The parser and lexical analyzer manage the computing linguistic conventional and context-free morphology.

Enhancement of FSM

Creating a system with the fewest number of phases that fulfills the same job is what maximizing an FSM entails. The Hopcroft minimization technique is the quickest called algorithm for achieving this. Another method is to use an inference list or the Moore reduction algorithm. Acyclic FSAs can also be reduced in sorted order.

Mathematical model

The below given formal activities are given in agreement with the broad categorization.

A deterministic finite-state machine (DFSM), sometimes known as a deterministic finite-state receiver, is a quadruple device (Σ, S, s0, δ, F).

Here,

Σ: It is the entry alphabet (a finite collection of characters that is not null).

S: It is a non-null finite subsequence.

s0: It is a first phase, a component of S.

δ: It's known as the state-transition function. Δ:S x Σ → S (It will be in a (NDFA) nondeterministic finite automaton δ: S x Σ → Ƥ(S)), such that δ would provide a collection of states).

F: It is the collection of final conditions, which is a (potentially null) subset of S.

ϵ It is common practice to enable δ to be a component operation in both deterministic and nondeterministic FSM, i.e., δ (s, x) isn't to be specified for every permutation of S ϵ S and x ϵ Σ. If an FSM M is in the phase s, the next sign is x, and δ (s, x) is not specified, M might report an issue (i.e., reject the input). This is important in typical state machine formulations, although less when altering the system. In their standard structure, several procedures may need total functions.

A finite-state machine has the similar computing capacity as a Turing computer, but its head can only conduct "read" actions and must always travel from left to right. That is, any basic phrase that a finite-state system accepts is also recognized by a limited Turing machine, and conversely.

A sextuple finite-state transducer (Σ, Г, S, s0, δ, ω), where

Σ: It is the entry alphabet (a limited collection of characters that is not null);

Г: It is the outgoing alphabet (a limited collection of signs that is not null);

S: It is a non-null finite set of objects.

s0: It is the first phase, a component of S;

δ: is the variable of initial state;

ω: It is the operation that produces results.

If the output function is determined by the stage and intake sign (ω: S x Σ → Г), that description conforms to the Mealy paradigm and may be represented as a Mealy device. If the output system is defined reliant on the state (ω: S → Г) then description conforms to the Moore model and may be described as a Moore device. A semi-automaton or transition machine is a (FSM) finite-state machine with no final output.

If the initial output sign of a Moore machine ω (s0) is ignored, it may be easily transformed to an outcome Mealy machine by designating the objective function of every Mealy change (i.e., marking every boundary) with the output sign of the terminal Moore state.

Since a Mealy machine phase may have multiple output tags on its receiving phases, the opposite conversion is more difficult (edges). Each such phase must be divided into numerous Moore machine states, one for each occurrence output sign.