Basic Properties of Graph Theory

Properties of graph theory are basically used for characterization of graphs depending on the structures of the graph. Following are some basic properties of graph theory:

1 Distance between two vertices

Distance is basically the number of edges in a shortest path between vertex X and vertex Y. If there are many paths connecting two vertices, then the shortest path is considered as the distance between the two vertices. Distance between two vertices is denoted by d(X, Y).

Example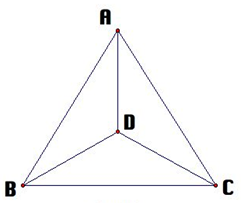

Suppose, we want to find the distance between vertex B and D, then first of all we have to find the shortest path between vertex B and D.

There are many paths from vertex B to vertex D:

• B -> C -> A -> D, length = 3
• B -> D, length = 1(Shortest Path)
• B -> A -> D, length = 2
• B -> C -> D, length = 2
• B -> C -> A -> D, length = 3

Hence, the minimum distance between vertex B and vertex D is 1.

2. Eccentricity of a vertex

Eccentricity of a vertex is the maximum distance between a vertex to all other vertices. It is denoted by e(V).

To count the eccentricity of vertex, we have to find the distance from a vertex to all other vertices and the highest distance is the eccentricity of that particular vertex.

Example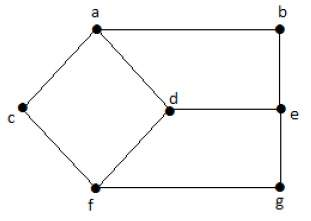

In the above example, if we want to find the maximum eccentricity of vertex 'a' then:

• The distance from vertex a to b is 1 (i.e. ab)
• The distance from vertex a to c is 1 (i.e. ac)
• The distance from vertex a to f is 2 (i.e. ac -> cf or ad -> df)
• The distance from vertex a to d is 1 (i.e. ad)
• The distance from vertex a to e is 2 (i.e. ab -> be or ad -> de)
• The distance from vertex a to g is 3 (i.e. ab -> be -> eg or ac -> cf -> fg etc.)

Hence, the maximum eccentricity of vertex 'a' is 3, which is a maximum distance from vertex ?a? to all other vertices.

Similarly, maximum eccentricities of other vertices of the given graph are:

• e(b) = 3
• e(c) = 3
• e(d) = 2
• e(e) = 3
• e(f) = 3
• e(g) = 3

3. Radius of connected Graph

The radius of a connected graph is the minimum eccentricity from all the vertices. In other words, the minimum among all the distances between a vertex to all other vertices is called as the radius of the graph. It is denoted by r(G).

Example

From the example of 5.2, r(G) = 2, which is the minimum eccentricity for the vertex 'd'.

4. Diameter of a Graph

Diameter of a graph is the maximum eccentricity from all the vertices. In other words, the maximum among all the distances between a vertex to all other vertices is considered as the diameter of the graph G. It is denoted by d(G).

Example

From the above example, if we see all the eccentricities of the vertices in a graph, we will see that the diameter of the graph is the maximum of all those eccentricities.

Diameter of graph d(G) = 3, which is the maximum eccentricity.

5. Central point

If the eccentricity of the graph is equal to its radius, then it is known as central point of the graph.

Or

If r(V) = e(V), then V is the central point of the graph G.

Example

From the above example, 'd' is the central point of the graph. i.e.

6. Centre

The set of all the central point of the graph is known as centre of the graph.

Example

From the example of 5.2, {'d'} is the centre of the graph.

7. Circumference

The total number of edges in the longest cycle of graph G is known as the circumference of G.

Example

In the above example, the circumference is 6, which is derived from the longest path a -> c -> f -> g -> e -> b -> a or a -> c -> f -> d -> e -> b -> a.

8. Girth

The total number of edges in the shortest cycle of graph G is known as girth. It is denoted by g(G).

Example

In the above example, the girth of the graph is 4, which is derived from the shortest cycle a -> c -> f -> d -> a, d -> f -> g -> e -> d or a -> b -> e -> d -> a.

9. Sum of degrees of vertices Theorem

For non-directed graph G = (V,E) where, Vertex set V = {V1, V2, .... Vn} then,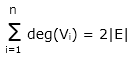

In other words, for any graph, the sum of degrees of vertices equals twice the number of edges.

Corollary 1

For directed graph G = (V, E) where, Vertex Set V = {V1, V2, ... Vn} then,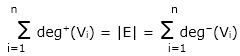

Corollary 2

The number of vertices in any non- directed graph with odd degree is even.

Example

It is impossible to make a graph with v (number of vertices) = 6 where the vertices have degrees 1, 2, 2, 3, 3, 4. This is because the sum of the degrees deg(V) is,

Corollary 3

In an non-directed graph, if the degree of each vertex is k, then

Corollary 4

If the degree of each vertex in a non-directed graph is at least k, then

Corollary 5

If the degree of each vertex in a non- directed graph is at most k, then