Connectivity

• Connectivity is a basic concept of graph theory. It defines whether a graph is connected or disconnected. Without connectivity, it is not possible to traverse a graph from one vertex to another vertex.
• A graph is said to be connected graph if there is a path between every pair of vertex. From every vertex to any other vertex there must be some path to traverse. This is called the connectivity of a graph.
• A graph is said to be disconnected, if there exists multiple disconnected vertices and edges.
• Graph connectivity theories are essential in network applications, routing transportation networks, network tolerance etc.

Example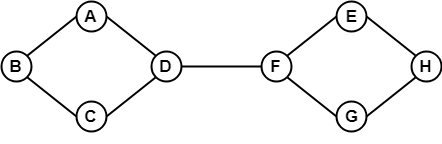

In the above example, it is possible to travel from one vertex to another vertex. Here, we can traverse from vertex B to H using the path B -> A -> D -> F -> E -> H. Hence it is a connected graph.

Example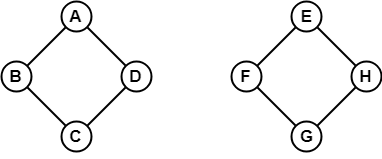

In the above example, it is not possible to traverse from vertex B to H because there is no path between them directly or indirectly. Hence, it is a disconnected graph.

Let's see some basic concepts of Connectivity.

1. Cut Vertex

A single vertex whose removal disconnects a graph is called a cut-vertex.

Let G be a connected graph. A vertex v of G is called a cut vertex of G, if G-v (Remove v from G) results a disconnected graph.

When we remove a vertex from a graph then graph will break into two or more graphs. This vertex is called a cut vertex.

Note: Let G be a graph with n vertices:

• A connected graph G may have maximum (n-2) cut vertices.
• Removing a cut vertex may leave a graph disconnected.
• Removing a vertex may increase the number of components in a graph by at least one.
• Every non-pendant vertex of a tree is a cut vertex.

Example 1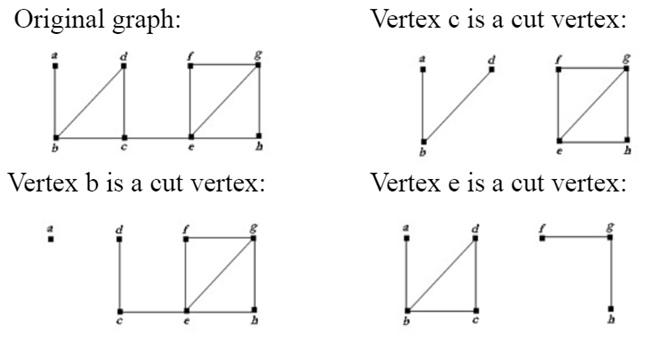

Example 2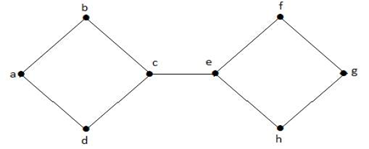

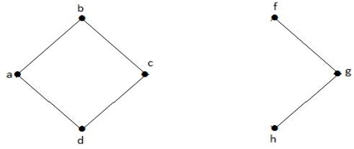
In the above graph, vertex 'e' is a cut-vertex. After removing vertex 'e' from the above graph the graph will become a disconnected graph.

2. Cut Edge (Bridge)

A cut- Edge or bridge is a single edge whose removal disconnects a graph.

Let G be a connected graph. An edge e of G is called a cut edge of G, if G-e (Remove e from G) results a disconnected graph.

When we remove an edge from a graph then graph will break into two or more graphs. This removal edge is called a cut edge or bridge.

Note: Let G be a graph with n vertices:

• A connected graph G may have at most (n-1) cut edges.
• Removing a cut edge may leave a graph disconnected.
• Removal of an edge may increase the number of components in a graph by at most one.
• A cut edge 'e' must not be the part of any cycle in G.
• If a cut edge exists, then a cut vertex must also exist because at least one vertex of a cut edge is a cut vertex.
• If a cut vertex exists, then the existence of any cut edge is not necessary.

Example 1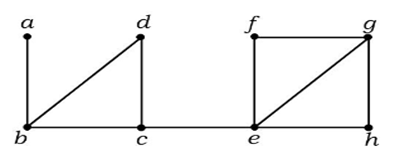

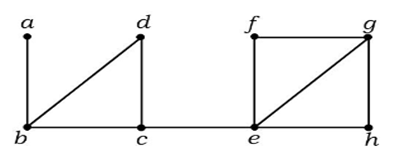
In the above graph, edge (c, e) is a cut-edge. After removing this edge from the above graph the graph will become a disconnected graph.

Example 2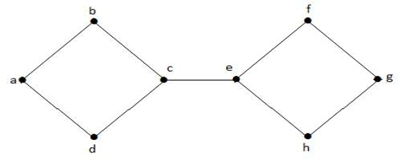

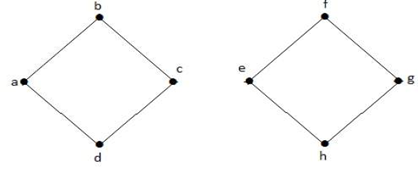
In the above graph, edge (c, e) is a cut-edge. After removing this edge from the above graph the graph will become a disconnected graph.

3. Cut Set

In a connected graph G, a cut set is a set S of edges with the following properties:

• The removal of all the edges in S disconnects G.
• The removal of some of edges (but not all) in S does not disconnect G.

Example 1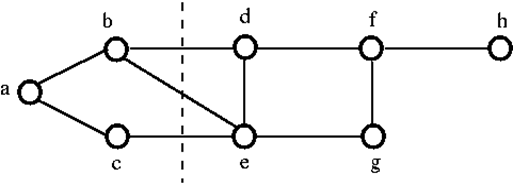

To disconnect the above graph G, we have to remove the three edges. i.e. bd, be and ce. We cannot disconnect it by removing just two of three edges. Hence, {bd, be, ce} is a cut set.

After removing the cut set from the above graph, it would look like as follows: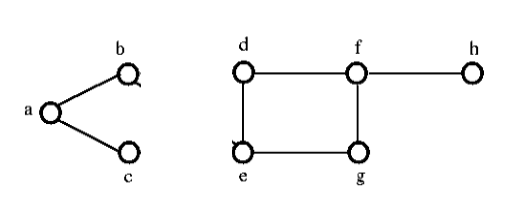

4. Edge Connectivity

The edge connectivity of a connected graph G is the minimum number of edges whose removal makes G disconnected. It is denoted by λ(G).

When λ(G) ≥ k, then graph G is said to be k-edge-connected.

Example

Let's see an example,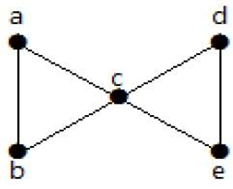

From the above graph, by removing two minimum edges, the connected graph becomes disconnected graph. Hence, its edge connectivity is 2. Therefore the above graph is a 2-edge-connected graph.

Here are the following four ways to disconnect the graph by removing two edges: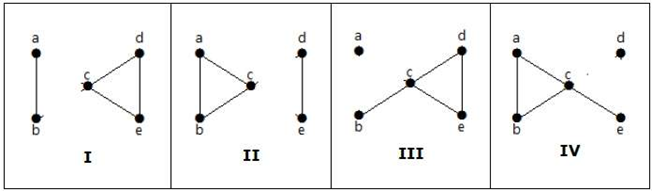

5. Vertex Connectivity

The connectivity (or vertex connectivity) of a connected graph G is the minimum number of vertices whose removal makes G disconnects or reduces to a trivial graph. It is denoted by K(G).

The graph is said to be k- connected or k-vertex connected when K(G) ≥ k. To remove a vertex we must also remove the edges incident to it.

Example

Let's see an example: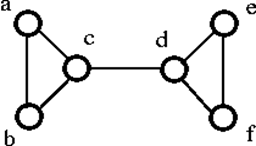

The above graph G can be disconnected by removal of the single vertex either 'c' or 'd'. Hence, its vertex connectivity is 1. Therefore, it is a 1-connected graph.