Coverings

A graph covering of a graph G is a sub-graph of G which contains either all the vertices or all the edges corresponding to some other graph.

A sub-graph which contains all the vertices is called a line/edge covering. A sub-graph which contains all the edges is called a vertex covering.

1. Edge Covering

A set of edges which covers all the vertices of a graph G, is called a line cover or edge cover of G.

Edge covering does not exist if and only if G has an isolated vertex.

Edge covering of graph G with n vertices has at least n/2 edges.

Example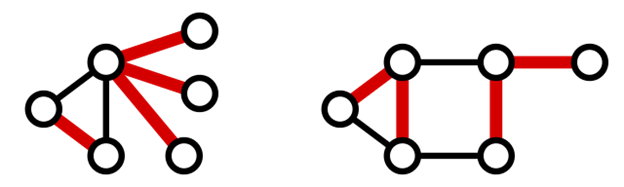

In the above graph, the red edges represent the edges in the edge cover of the graph.

Minimal Line covering

A line covering M of a graph G is said to be minimal line cover if no edge can be deleted from M.

Or minimal edge cover is an edge cover of graph G that is not a proper subset of any other edge cover.

No minimal line covering contains a cycle.

Example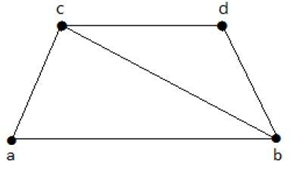

From the above graph, the sub-graph having edge covering are:

M1 = {{a, b}, {c, d}}
M2 = {{a, d}, {b, c}}
M3 = {{a, b}, {b, c}, {b, d}}
M4 = {{a, b}, {b, c}, {c, d}}

Here, M₁, M₂, M₃ are minimal line coverings, but M₄ is not because we can delete {b, c}.

Minimum Line Covering

A minimal line covering with minimum number of edges is called a minimum line covering of graph G. It is also called smallest minimal line covering.

Every minimum edge cover is a minimal edge cove, but the converse does not necessarily exist.

The number of edges in a minimum line covering in G is called the line covering number of G and it is denoted by α₁.

Example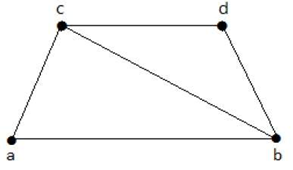

From the above graph, the sub-graph having edge covering are:

M1 = {{a, b}, {c, d}}
M2 = {{a, d}, {b, c}}
M3 = {{a, b}, {b, c}, {b, d}}
M4 = {{a, b}, {b, c}, {c, d}}

In the above example, M₁ and M₂ are the minimum edge covering of G and α₁ = 2.

2. Vertex Covering

A set of vertices which covers all the nodes/vertices of a graph G, is called a vertex cover for G.

Example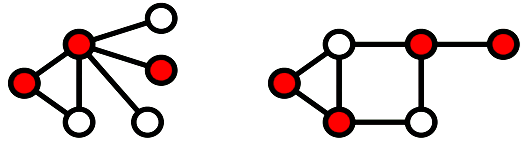

In the above example, each red marked vertex is the vertex cover of graph. Here, the set of all red vertices in each graph touches every edge in the graph.

Minimal Vertex Covering

A vertex M of graph G is said to be minimal vertex covering if no vertex can be deleted from M.

Example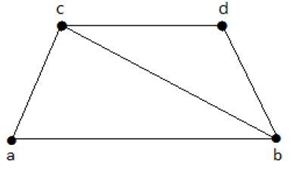

The sub- graphs that can be derived from the above graph are:

M1 = {b, c}
M2 = {a, b, c}
M3 = {b, c, d}

Here, M₁ and M₂ are minimal vertex coverings, but in M₃ vertex 'd' can be deleted.

Minimum Vertex Covering

A minimal vertex covering is called when minimum number of vertices are covered in a graph G. It is also called smallest minimal vertex covering.

The number of vertices in a minimum vertex covering in a graph G is called the vertex covering number of G and it is denoted by α₂.

Example 1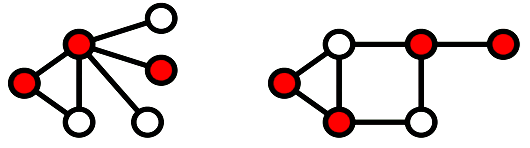

In the above graphs, the vertices in the minimum vertex covered are red.

α₂ = 3 for first graph.

And α₂ = 4 for the second graph.

Example 2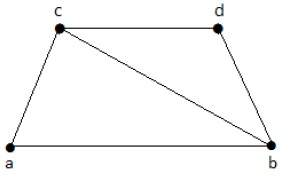

The sub- graphs that can be derived from the above graph are:

M1 = {b, c}
M2 = {a, b, c}
M3 = {b, c, d}

Here, M1 is a minimum vertex cover of G, as it has only two vertices. Therefore, α₂ = 2.