Graph Representations

In graph theory, a graph representation is a technique to store graph into the memory of computer.

To represent a graph, we just need the set of vertices, and for each vertex the neighbors of the vertex (vertices which is directly connected to it by an edge). If it is a weighted graph, then the weight will be associated with each edge.

There are different ways to optimally represent a graph, depending on the density of its edges, type of operations to be performed and ease of use.

1. Adjacency Matrix

Adjacency matrix is a sequential representation.
It is used to represent which nodes are adjacent to each other. i.e. is there any edge connecting nodes to a graph.
In this representation, we have to construct a nXn matrix A. If there is any edge from a vertex i to vertex j, then the corresponding element of A, aⁱ,^j = 1, otherwise aⁱ,^j= 0.

Note, even if the graph on 100 vertices contains only 1 edge, we still have to have a 100x100 matrix with lots of zeroes.

If there is any weighted graph then instead of 1s and 0s, we can store the weight of the edge.

Example

Consider the following undirected graph representation:

Undirected graph representation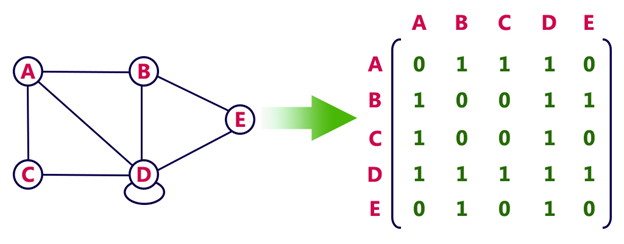

Directed graph represenation

See the directed graph representation: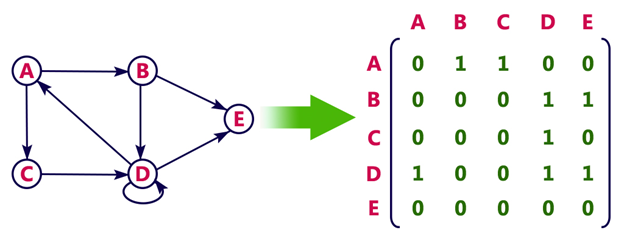

In the above examples, 1 represents an edge from row vertex to column vertex, and 0 represents no edge from row vertex to column vertex.

Undirected weighted graph represenation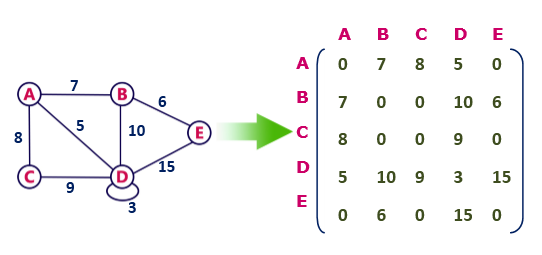

Pros: Representation is easier to implement and follow.

Cons: It takes a lot of space and time to visit all the neighbors of a vertex, we have to traverse all the vertices in the graph, which takes quite some time.

2. Incidence Matrix

In Incidence matrix representation, graph can be represented using a matrix of size:

Total number of vertices by total number of edges.

It means if a graph has 4 vertices and 6 edges, then it can be represented using a matrix of 4X6 class. In this matrix, columns represent edges and rows represent vertices.

This matrix is filled with either 0 or 1 or -1. Where,

0 is used to represent row edge which is not connected to column vertex.
1 is used to represent row edge which is connected as outgoing edge to column vertex.
-1 is used to represent row edge which is connected as incoming edge to column vertex.

Example

Consider the following directed graph representation.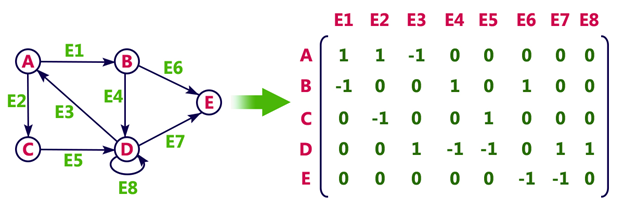

3. Adjacency List

Adjacency list is a linked representation.
In this representation, for each vertex in the graph, we maintain the list of its neighbors. It means, every vertex of the graph contains list of its adjacent vertices.
We have an array of vertices which is indexed by the vertex number and for each vertex v, the corresponding array element points to a singly linked list of neighbors of v.

Example

Let's see the following directed graph representation implemented using linked list: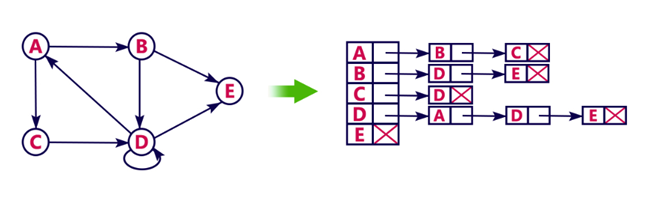

We can also implement this representation using array as follows: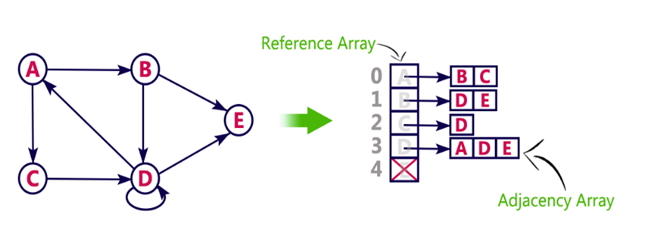

Pros:

Adjacency list saves lot of space.
We can easily insert or delete as we use linked list.
Such kind of representation is easy to follow and clearly shows the adjacent nodes of node.

Cons: