Tree and Forest

1. What is Tree and Forest?

Tree

• In graph theory, a tree is an undirected, connected and acyclic graph. In other words, a connected graph that does not contain even a single cycle is called a tree.
• A tree represents hierarchical structure in a graphical form.
• The elements of trees are called their nodes and the edges of the tree are called branches.
• A tree with n vertices has (n-1) edges.
• Trees provide many useful applications as simple as a family tree to as complex as trees in data structures of computer science.
• A leaf in a tree is a vertex of degree 1 or any vertex having no children is called a leaf.

Example

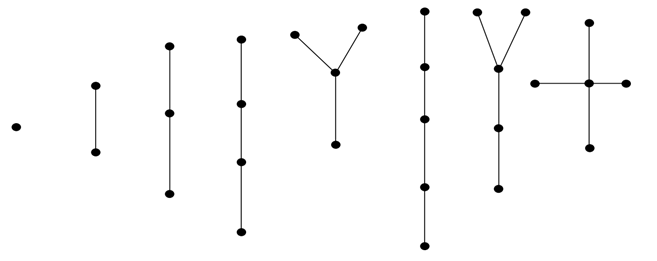
In the above example, all are trees with fewer than 6 vertices.

Forest

In graph theory, a forest is an undirected, disconnected, acyclic graph. In other words, a disjoint collection of trees is known as forest. Each component of a forest is tree.

Example

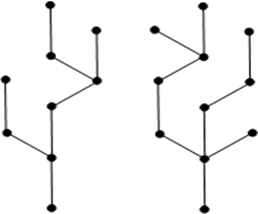
The above graph looks like a two sub-graphs but it is a single disconnected graph. There are no cycles in the above graph. Therefore it is a forest.

2. Properties of Trees

1. Every tree which has at least two vertices should have at least two leaves.
2. Trees have many characterizations:
   Let T be a graph with n vertices, then the following statements are equivalent:
   • T is a tree.
   • T contains no cycles and has n-1 edges.
   • T is connected and has (n -1) edge.
   • T is connected graph, and every edge is a cut-edge.
   • Any two vertices of graph T are connected by exactly one path.
   • T contains no cycles, and for any new edge e, the graph T+ e has exactly one cycle.
3. Every edge of a tree is cut -edge.
4. Adding one edge to a tree defines exactly one cycle.
5. Every connected graph contains a spanning tree.
6. Every tree has at least two vertices of degree two.

3. Spanning Tree

A spanning tree in a connected graph G is a sub-graph H of G that includes all the vertices of G and is also a tree.

Example

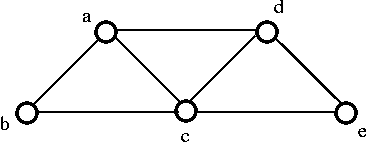
Consider the following graph G:

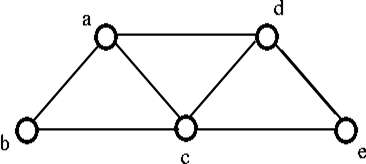
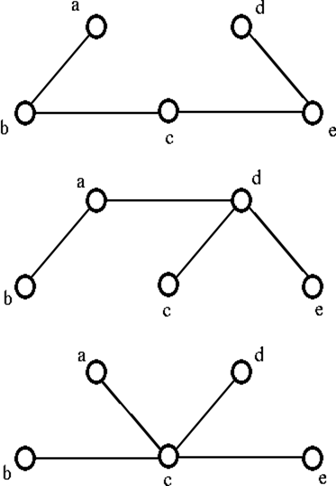
From the above graph G we can implement following three spanning trees H:

Methods to find the spanning Tree

We can find the spanning tree systematically by using either of two methods:

1. Cutting- down Method
2. Building- up Method

1. Cutting- down method

• Start choosing any cycle in Graph G.
• Remove one of cycle's edges.
• Repeat this process until there are no cycles left.

Example

• Consider a graph G,

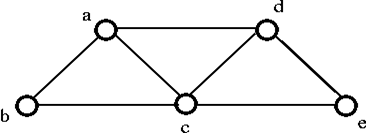
• If we remove the edge ac which destroy the cycle a-d-c-a in the above graph then we get the following graph:

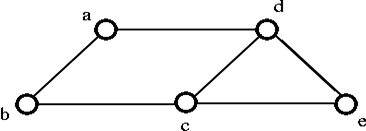
• Remove the edge cb, which destroy the cycle a-d-c-b-a from the above graph then we get the following graph:

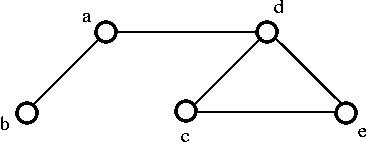
• If we remove the edge ec, which destroy the cycle d-e-c-d from the above graph then we get the following spanning tree:

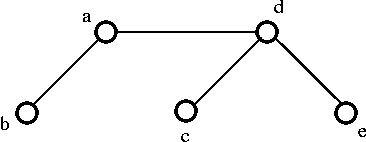
2. Building - up method

• Select edges of graph G one at a time. In such a way that there are no cycles are created.
• Repeat this process until all the vertices are included.

Example

Consider the following graph G,

• Choose the edge ab,

• Choose the edge de,

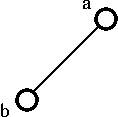
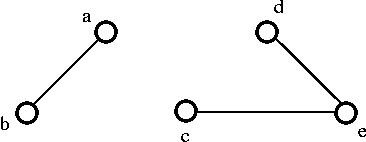
• After that , choose the edge ec,

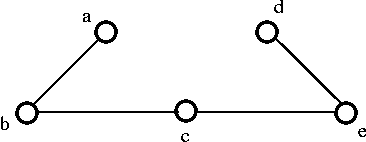
• Next, choose the edge cb, then finally we get the following spanning tree:

Circuit Rank

The number of edges we need to delete from G in order to get a spanning tree.

Spanning tree G = m- (n-1), which is called the circuit rank of G.

Example

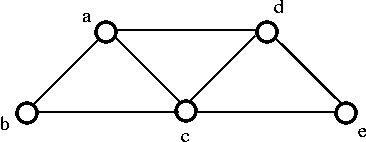
In the above graph, edges m = 7 and vertices n = 5

Then the circuit rank is,