Graphing Functions in Discrete mathematics

Graphing function can be described as a process of drawing the graph of a function. There are some simple functions and some complex functions in the basic graphing functions. The simple functions are cubic, linear, quadratic, and many more and the complex functions are logarithmic, rational, etc. In this section, we will understand the definition, basic functions, and examples of graphing functions.

Use of Graphing functions

With the help of a graphical function, we can draw a curve that is used to indicate the function on a coordinate plane. If this curve (graph) indicates a function, then each and every point on the curve will equally satisfy the function. For example: In this graph, we will show the linear function f(x) = -x+2.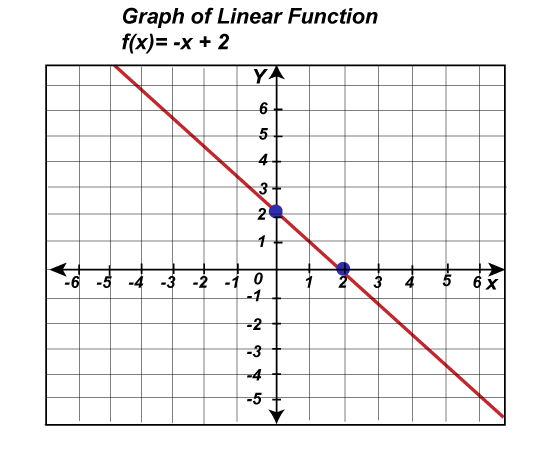

Now we can take any point on the line from the above graph. Here we will take (-1, 3). Now we will substitute (-1, 3) = (x, y) in the function f(x) = -x+2. That means for this function, x = -1, and y = 3. We can also write the function f(x) = -x+2 in the form y = -x+2.

Now we will put the values of x and y in the function y = -x+2 and get the following:

3 = -(-1)+2

3 = 1+2

3 = 3

Hence, we can say that the point (-1, 3) satisfies the function.

Similarly, we can take different points from the above line and check whether those points satisfy the function. In this case, the function will be satisfied by every point on the line/curve. The process of drawing these types of curves, which represent the functions, is known as graphing functions.

Graphing Basic function

There are a lot of basic graphic functions that are very easy, i.e., quadratic functions and linear functions. Some basic ideas of graphical functions are described as follows:

• If it is possible to identify the shape, then we will first do it. For example: The given graph will be a line if it is a linear function with the form f(x) = ax+b. The given graph will be a parabola if it is a quadratic function which has a form f(x) = ax² + bx + c.
• We can determine some points on it with the help of substituting some random values of x and then substituting each value into the function to determine the corresponding values of y.

Now we will understand some examples of graphing basis functions with the help of graphical linear functions, Graphical quadratic functions, and Graphical complex functions.

Graphical Linear Functions

We have already drawn a graph for a linear function with the form f(x) = ax+b. Here we will also take the same linear form. Here we will create a table with some random values of x. So we will take some values like x = 0 and x = 1, and then we will find the value of y by putting each of the values of x in y = -x+2. After putting the values, we will get the following:

So from the above, we get two points on the line that is (0, 2) and (1, 1). If we plot any of the one points on a graph and join these points with the help of a straight line (extending the line on both sides), then the graph will be the same as shown above.

Graphical Quadratic functions

In this function, we can also determine some random points on it. With the help of these random values, we may not get a perfect U-shaped curve because if we want to get a perfect U-shaped curve, then we have to know about the point where the curve is turning. That means for a perfect U-shaped curve, we have to find its vertex. When we successfully find the vertex, we identify two or three random points on each side of the vertex. These random points will help us to draw the graph of a function.

Example: In this example, we have to draw a graph of the quadratic function, which has a line f(x) = x² - 2x + 5.

Solution: First, we will compare f(x) = x²-2x+5 with f(x) = ax²+bx+c, and then we will get a = 1, b = -2, and c = 5.

Now we will get the coordinate of x axis and y axis with the help of these values.

The x coordinates of vertex will be

h = -b /2a = -(-2) /2(1) = 1.

The y coordinates of the vertex will be

f(1) = 1² - 2(1) + 5 = 4.

Hence, the x and y coordinates of the vertex will be (1, 4).

Now we will create a table by taking two random numbers of x on each side of 1. Then we will use the above function y = x²-2x+5, and find the y coordinates.

With the help of above table, the plots will be (-1, 8), (0, 5), (1, 4), (2, 5), and (3, 8). Now we will join all the points on the graph sheet and extend the curve on both sides like this: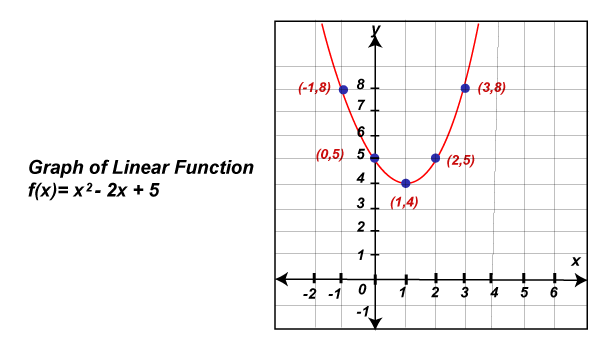

Graphical Complex Functions

The graphing function will be known as the simplest function if each of their range and domain is a set of real numbers. This case is not compulsory for all types of functions. There can be complex functions for which we have to take care about the range, domain, holes, and asymptotes at the time of drawing them. The most popular those types of functions are described as follows:

• Rational Functions: The parent function of rational function must be in the form f(x) = 1/x. The rational function can also be known as the reciprocal function.
• Exponential Functions: The parent function of exponential function must be in the form f(x) = a^x.
• Logarithmic Functions: The parent function of logarithmic function must be in the form f(x) = log x.

Now we will show the graph of each of the function's parent functions separately like this: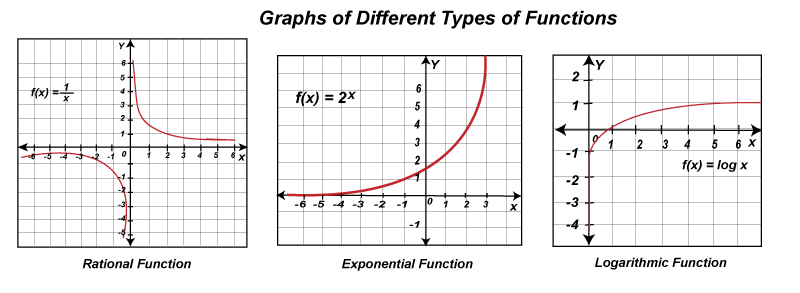

We have to follow the following steps in each of these cases for graphing functions:

• First, we will find out the domain and range of the function, and with the help of them, we will draw the curve.
• After that, we will determine the x-intercepts(s) and y-intercepts(s) and then plot them.
• Determine whether there is any hole.
• After that, we will determine the asymptotes (horizontal, vertical, and slant) and draw them with the help of dotted lines so that the graph can be break along those lines. While doing this, we have to take care that the graph does not touch them.
• Now, we will make a table with the help of taking some random values of x (on both sides of x-intercept and/or on both sides of vertical asymptote). Then by these values, we will find out the corresponding values of y.
• We will plot the points from the table. For this, we will join them on the basis of their range, domain, and asymptotes.

We will use the Graphical rational functions, Graphical exponential functions, and Graphical logarithmic functions to understand the graph of a function in different cases with the help of above steps.

Graphing Rational functions

Here we will graph a rational function f(x) = (x+1) /(x-2) with the help of above steps like this:

• From the above rational function, the domain = {x ∈ R | x ≠ 2} and Range = {y ∈ R | y ≠ 1}. Now we will determine the domain and range of a rational function.
• The x-intercept of this rational function is (-1, 0), and y-intercept of this function is (0, -0.5).
• It does not contain any holes.
• Vertical asymptote (VA) of this function is x = 2, and horizontal asymptote (VA) of this function is y = 1.
• Now, on both sides of vertical asymptote x = 2, we will take some random values, and then we will find out the respective value of y like this:

Now we will plot all the above points along with Horizontal asymptote (HA) and vertical asymptote (VA) in the following way: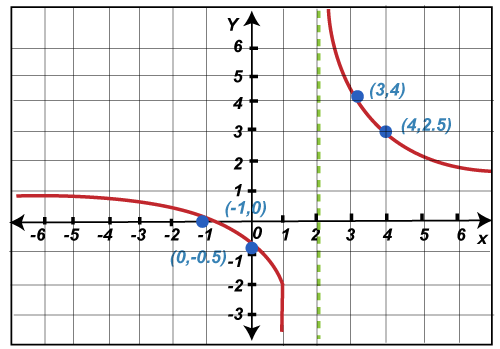

Graphing Exponential Functions

Here we will assume an exponential function f(x) = 2^-x + 2. With the help of steps described in the Graphical complex functions, we will graph this function like this:

• The domain of this function is the set of all real numbers (R), and the range of this function is y > 2.
• This function has a horizontal asymptote at y = 2, but it does not have any vertical asymptote.
• It has a y-intercept which is (0, 3), but it does not have any x-intercepts.
• It also does not have any holes.
• So lastly, we don't have any data related to x-intercept and VA (vertical asymptote). We only have data related to the y-intercept, which is (0, 3). On both sides of x = 0, we will take some random values and then frame a table with the help of these values like this:

Now we will plot all the above information on a graph in the following way: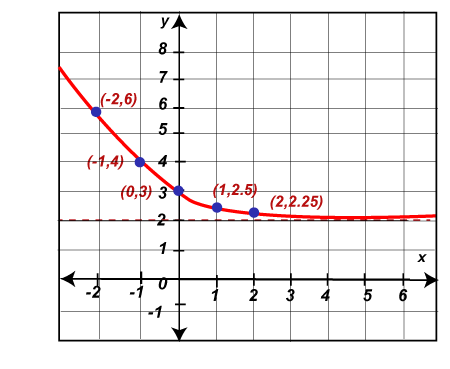

Graphical Logarithmic Functions

Here we will assume a logarithmic function f(x) = 2 log₂ x-2. With the help of steps described in the Graphical complex functions, we will graph this function like this:

• The domain of this function is x>0, and the range of this function is the set of all real numbers (R).
• The x-int of this function is (2, 0), but this function does not have any y int.
• The vertical asymptote of this function is y = 0 (x-axis), and it does not contain any horizontal asymptote.
• It also does not have any holes.
• So lastly, we only have one reference point, i.e., (2, 0). On both sides of 0, we will take some random values and then frame a table with the help of these values. We cannot take the value of x less than 0 because the domain is x>0.

Here we have chosen those types of x's values that are able to simplify the value of y easily.

Now we will plot all the above information on a graph in the following way: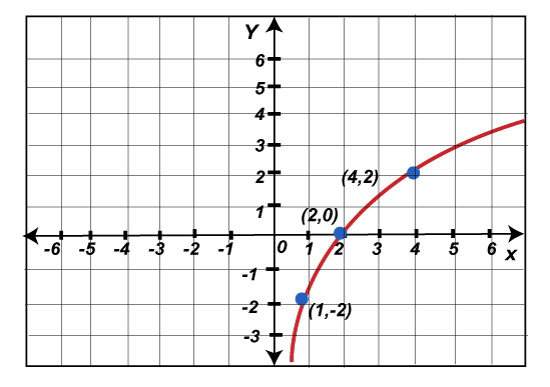

Graphing Functions by Transformations

We can graph the functions with the help of applying transformations on the graph of parent functions. Here we will show some parents functions of some important functions like this:

Linear function: Its parent function is: f(x) = x

Quadratic function: Its parent functions is: f(x) = x²

Cubic function: Its parent functions is: f(x) = x³

Absolute Value function: Its parent function is: f(x) = |x|

Reciprocal function: Its parent function is: f(x) = 1/x

Logarithm function: Its parent function is: f(x) = log x

Square root function: Its parent function is: √x

Cube root function: Its parent function is: ∛x

Exponential function: f(x) = a^x, 0<a<1

We should keep in mind the look of the graph of all above-described parent functions. After that, we will be able to apply the transformation to the graph of given function.

Important Notes on Graphing Functions

• In the graphing function, f(ax) ≠ a f(x). There may be different values for both.
• The asymptotes will never be touched by the graph of a function.
• The value of x can be a decimal number, real number, or whole number, which we use to plot any function f(x).
• We should not choose those types of values of x in the table that does not have a function's domain.