Heap Data Structure

What is Heap?

A heap is a complete binary tree, and the binary tree is a tree in which the node can have utmost two children. Before knowing more about the heap data structure, we should know about the complete binary tree.

What is a complete binary tree?

A complete binary tree is a binary tree in which all the levels except the last level, i.e., leaf node should be completely filled, and all the nodes should be left-justified.

Let's understand through an example.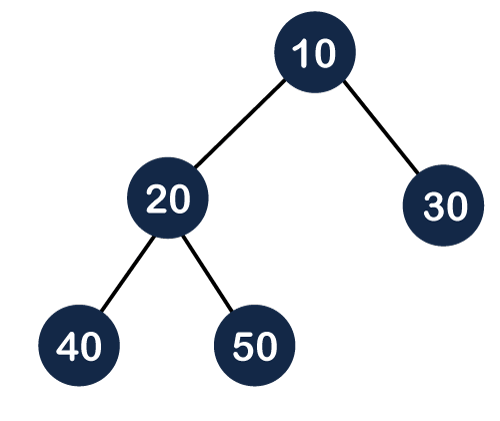

In the above figure, we can observe that all the internal nodes are completely filled except the leaf node; therefore, we can say that the above tree is a complete binary tree.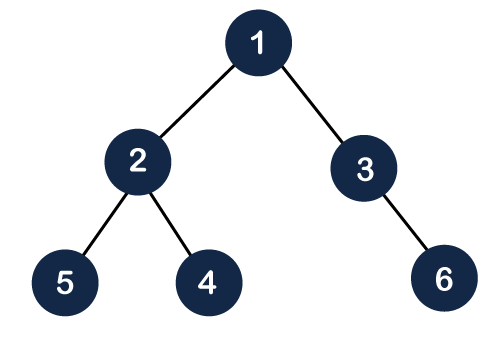

The above figure shows that all the internal nodes are completely filled except the leaf node, but the leaf nodes are added at the right part; therefore, the above tree is not a complete binary tree.

Note: The heap tree is a special balanced binary tree data structure where the root node is compared with its children and arrange accordingly.

How can we arrange the nodes in the Tree?

There are two types of the heap:

• Min Heap
• Max heap

Min Heap: The value of the parent node should be less than or equal to either of its children.

Or

In other words, the min-heap can be defined as, for every node i, the value of node i is greater than or equal to its parent value except the root node. Mathematically, it can be defined as:

A[Parent(i)] <= A[i]

Let's understand the min-heap through an example.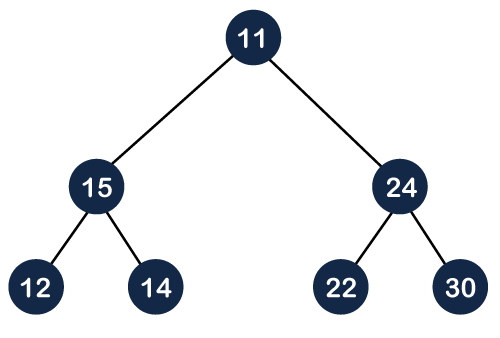

In the above figure, 11 is the root node, and the value of the root node is less than the value of all the other nodes (left child or a right child).

Max Heap: The value of the parent node is greater than or equal to its children.

Or

In other words, the max heap can be defined as for every node i; the value of node i is less than or equal to its parent value except the root node. Mathematically, it can be defined as:

A[Parent(i)] >= A[i]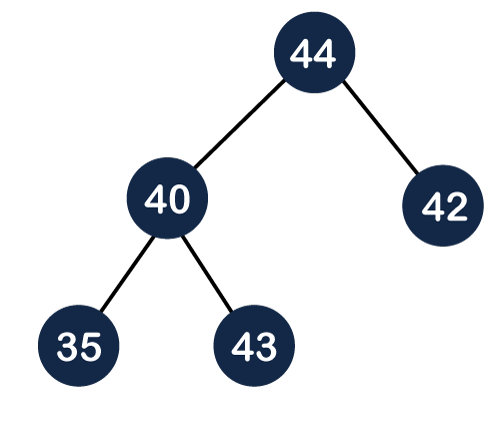

The above tree is a max heap tree as it satisfies the property of the max heap. Now, let's see the array representation of the max heap.

Time complexity in Max Heap

The total number of comparisons required in the max heap is according to the height of the tree. The height of the complete binary tree is always logn; therefore, the time complexity would also be O(logn).

Algorithm of insert operation in the max heap.

Let's understand the max heap through an example.

In the above figure, 55 is the parent node and it is greater than both of its child, and 11 is the parent of 9 and 8, so 11 is also greater than from both of its child. Therefore, we can say that the above tree is a max heap tree.

Insertion in the Heap tree

44, 33, 77, 11, 55, 88, 66

Suppose we want to create the max heap tree. To create the max heap tree, we need to consider the following two cases:

• First, we have to insert the element in such a way that the property of the complete binary tree must be maintained.
• Secondly, the value of the parent node should be greater than the either of its child.

Step 1: First we add the 44 element in the tree as shown below:

Step 2: The next element is 33. As we know that insertion in the binary tree always starts from the left side so 44 will be added at the left of 33 as shown below:

Step 3: The next element is 77 and it will be added to the right of the 44 as shown below: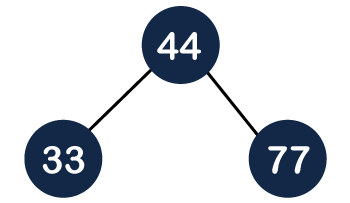

As we can observe in the above tree that it does not satisfy the max heap property, i.e., parent node 44 is less than the child 77. So, we will swap these two values as shown below: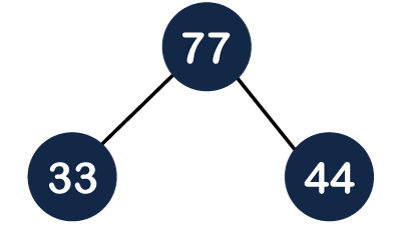

Step 4: The next element is 11. The node 11 is added to the left of 33 as shown below: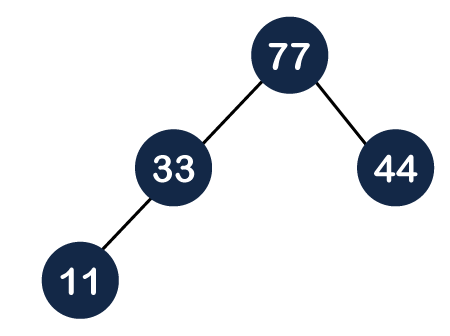

Step 5: The next element is 55. To make it a complete binary tree, we will add the node 55 to the right of 33 as shown below: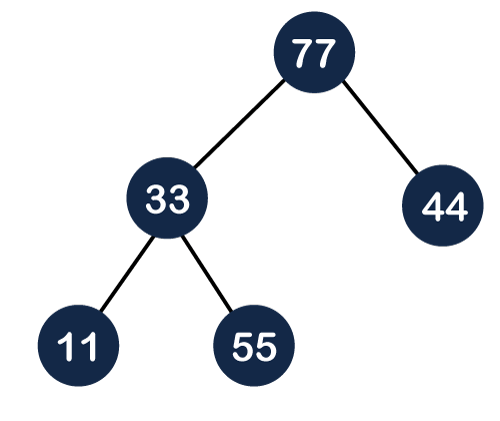

As we can observe in the above figure that it does not satisfy the property of the max heap because 33<55, so we will swap these two values as shown below: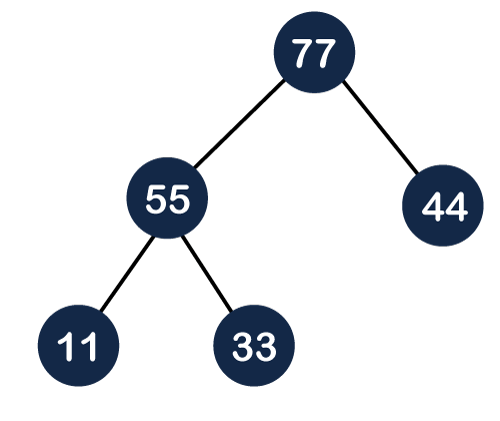

Step 6: The next element is 88. The left subtree is completed so we will add 88 to the left of 44 as shown below: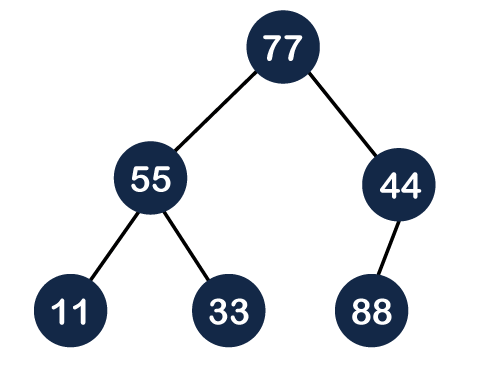

As we can observe in the above figure that it does not satisfy the property of the max heap because 44<88, so we will swap these two values as shown below:

Again, it is violating the max heap property because 88>77 so we will swap these two values as shown below:

Step 7: The next element is 66. To make a complete binary tree, we will add the 66 element to the right side of 77 as shown below:

In the above figure, we can observe that the tree satisfies the property of max heap; therefore, it is a heap tree.

Deletion in Heap Tree

In Deletion in the heap tree, the root node is always deleted and it is replaced with the last element.

Let's understand the deletion through an example.

Step 1: In the above tree, the first 30 node is deleted from the tree and it is replaced with the 15 element as shown below:

Now we will heapify the tree. We will check whether the 15 is greater than either of its child or not. 15 is less than 20 so we will swap these two values as shown below:

Again, we will compare 15 with its child. Since 15 is greater than 10 so no swapping will occur.

Algorithm to heapify the tree