Hermitian matrix in Discrete mathematics

The symmetric matrix and the Hermitian matrix are both used to contain similar properties. The name Hermitian was placed after a famous mathematician Charles Hermite. The Hermitian matrix is used to contain complex numbers in the form of its elements. The Hermitian matrix will be similar to its conjugate transpose matrix. The conjugate transpose of a matrix A can be indicated by the symbol A^H or A∗. In this section, we are going to learn about the Hermitian matrix, Hermitian matrix with different orders, its formula, its properties, examples of the Hermitian matrix and many more.

What is Hermitian matrix

A matrix will be known as the Hermitian matrix if there is a square matrix which is similar to its conjugate transpose matrix. In case of a Hermitian matrix, all the non-diagonal elements will contain the complex numbers, and all its diagonal elements will contain the real numbers. In this type of matrix, all the complex numbers will be arranged in the way that elements of ith row and jth column will be the complex conjugate of the element of jth row and ith column. If there is a number, which is indicated by a+ib, then that number will be a complex number, where a is used to indicate the real part and b is used to indicate the imaginary part.

A matrix will be known as the Hermitian matrix if it contains the condition, i.e., A = A^H. The symmetric matrix and the Hermitian matrix are both similar to each other, but there is one difference, i.e., the Hermitian matrix is used to contain the complex numbers in the non-principal diagonal elements.

Hermitian matrix of Order 2∗2

In case of a Hermitian matrix, the non-diagonal elements will be complex numbers. There will be real numbers in the first element of 1^st row and the second element of 2^nd row. In this matrix, the complex number of the second element of 1^st row will be a complex conjugate number of the first element of 2^nd row. The example of a Hermitian matrix with an order 2∗2 is described as follows: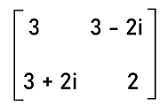

Hermitian matrix of order 3∗3

In case of a Hermitian matrix, the non-diagonal elements will be complex numbers. The real numbers will be contained by all those elements which connect the diagonal from first element of 1^st row to the third element of 3^rd row. The elements which are present at the position (i, j) will be known as the complex conjugate of the element which is present at the position (j, i). The example to indicate the Hermitian matrix is described as follows: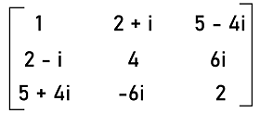

The 1^st row and 2^nd column of this matrix contain the 2+i elements, whereas the 2^nd row and 1^st column of this matrix contain its conjugate element 2-i. All the other complex numbers will also contain the same case.

Formula of Hermitian matrix

With the help of above described two matrices, we know that the real numbers will be contained by the diagonal elements of the Hermitian matrix. We also know that the elements which exist at the position (i, j) will be the complex conjugate of the element which exists at the position (j, i). Hence the standard form to represent the Hermitian matrix with a 2∗2 is described as follows: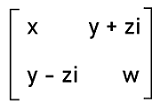

Here x, y, z, and w are used to indicate the real numbers.

Similarly, the standard form to represent the Hermitian matrix with an order 3∗3 is described as follows: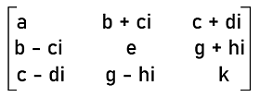

Properties of Hermitian matrix

There are various properties of a Hermitian matrix, and some of them are described as follows:

• In case of a Hermitian matrix, all the principal diagonal elements will always contain the real numbers.
• There must be complex numbers in the non-diagonal elements.
• If there is a Hermitian matrix, then that matrix must be a normal matrix like A^H = A.
• If we perform the addition of two Hermitian matrices, then the resultant matrix will be a Hermitian matrix.
• If we perform the inverse of two Hermitian matrices, then the resultant matrix will be a Hermitian matrix.
• If we perform the multiplication of two Hermitian matrices, then the resultant matrix will be a Hermitian matrix.
• If we calculate the determinant of a Hermitian matrix, then the matrix will be real.
• The eigenvalues are used to contain the real numbers in the Hermitian matrix.

Terms related to Hermitian matrix

There are some important points which we should know while learning the concept of a Hermitian matrix. These points are described as follows:

Principal diagonal: If there is a square matrix, then the principal diagonal can be indicated by all the sets of diagonal elements, which are connected from the first elements of 1^st row to the last element of last row.

Symmetric matrix: A square matrix can be called the symmetric matrix if we calculate the transpose of that matrix and both the matrices remains unchanged.

Conjugate matrix: If we replace the corresponding elements of given matrix with their corresponding elements, then we will be able to get the conjugate matrix of that matrix.

Transpose matrix: A matrix will be known as the transpose matrix if we interchange the elements of rows or columns of the original matrix. Suppose there is a square matrix A. We can indicate the transpose of this matrix with the help of symbol A^T.

Writing matrix as Hermitian and Skew-Hermitian

If there is a square matrix, then we can write this matrix as the addition of a Hermitian matrix P and skew-Hermitian matrix Q. With the help of following formula, we can determine the addition of a skew-Hermitian matrix and Hermitian matrix.

Suppose there is a square matrix A. Then,

A = (1/2) (A + A^H) + (1/2) (A - A^H). Here A^H is used to indicate the transpose of conjugate matrix A.

• If a Hermitian matrix is indicated by A + A^H, then (1/2) × (A + A^H) will also indicate a Hermitian matrix.
• If a skew-Hermitian matrix is indicated by A - A^H, then (1/2) × (A - A^H) will also indicate a skew-Hermitian matrix.

Hence if there is a square matrix, then we can write this matrix as the addition of a skew-Hermitian matrix and Hermitian matrix.

Examples of Hermitian matrix

There are a lot of examples of Hermitian matrices, and some of them are described as follows:

Example 1: In this example, we have a matrix A, and we have to determine whether it is a Hermitian matrix. The elements of matrix A are described as follows: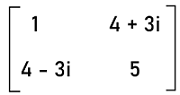

Solution: From the question, we have matrix A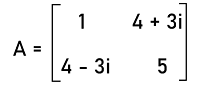

Now we will do the conjugate of this matrix like this: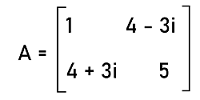

Now we will do the transpose of conjugate of A in the following way: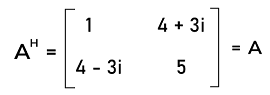

Hence the given matrix A is a Hermitian matrix.

Example 2: In this example, we have a Hermitian matrix, and we have to show that the determinant of this matrix will always be a real number.

Solution: For this, we will assume a 2∗2 Hermitian matrix, and we will determine its determinant.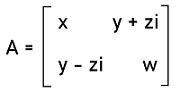

det A = xw - (y + zi)(y - zi)

= xw - (y²- z²i²)

= xw - (y²+ z²)

= xw - y²- z²

= a real number

In the same way, we can assume a Hermitian matrix with some other order and see that the determinant of that matrix is also a real number.

Hence it is proved that the determinant of a Herminant matrix is always a real number.

Example 3: In this example, we have two Hermitian matrices, and we have to determine the addition of these two matrices. We have to also prove that the output of this addition is also a Hermitian matrix. The elements of these two Hermitian matrices are described as follows: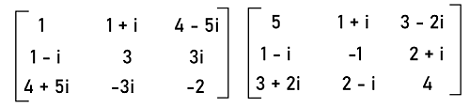

Solution: From the question, we have two Hermitian matrices and we will add both of them like this: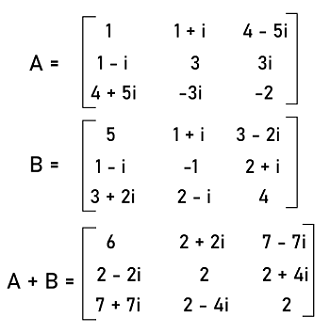

Now we will do the conjugate of the above addition (A+B) is described as follows: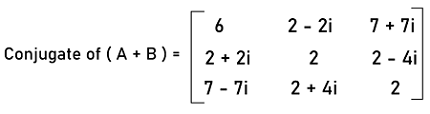

Now we will do the transpose of conjugate of A+B in the following way: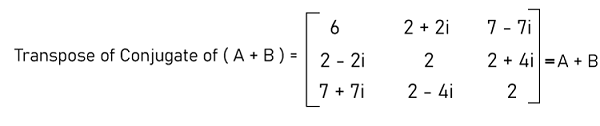

It is proved that the addition of two Hermitian matrices will also be a Hermitian matrix.

Example 4: In this example, we have a matrix A, and we have to determine whether it is a Hermitian matrix. The elements of matrix A are described as follows:

Solution: From the question, we have a Hermitian matrix, which is described as follows:

Now we will do the conjugate of matrix A in the following way:

Now we will do the conjugate transpose of A (A∗) in the following way:

Here we can see that the transpose conjugate of A and the given matrix A are similar to each other. Hence it is a Hermitian matrix.

Example 5: In this example, we have a Hermitian matrix A and a complex number x. Here we have to determine whether the multiplication of both xA will be a Hermitian matrix or not.

Solution: From the question, we know that there is a complex number x and a Hermitian matrix A, i.e., A∗ = A.

The multiplication of xA will be Hermitian if it satisfies the following condition:

(xA)∗ = xA

Now

(xA) = x̅A∗ = x̅A ≠ xA

Since x is used to indicate the complex number, which is not similar to its conjugate.

Hence

(xA)∗ = xA

Thus, xA will not be a Hermitian matrix.