How to Calculate volume of an object

In this tutorial, we will briefly learn the steps to calculate the volume of different objects.

Before we move further, let us understand the definition of a volume.

What is volume?

The volume of a shape is the measure of how much 3-D (three-dimensional) space any object occupies.

Volume is also defined by the capacity of water (or air, or sand, etc.,) that a shape could hold. As per the International System of Units (SI), if any object has its dimensions in meters, the standard volume will be cubic meters or m3. Volume is also measured in three different units, i.e., cubic centimeters or cm3, cubic inches or in3, and cubic feet or ft3.

Different objects hold different volumes. We have learned about different solid shapes in three-dimensional geometry, including cube, cuboid, pyramid, sphere, cylinder, cone, etc. Let us discover the step-by-step formula to calculate the volume for all these 3-D geometry shapes:

1. Calculating the Volume of a Cube

A cube is defined as a solid 3-D (three-dimensional) object that consists of six equal square sides. In other words, it is a box shape with identical faces all around. For example, the ludo dice is a cube as all the six sides of the cubes are identical.

Note: The cube has all identical sides of equal length, so without any second thought, you can pick any side to measure. If at any point you are sceptical and want to check whether the solid shape is a cube or not, measure each side of the object and determine if they are equal or not.

Formula

Formula 1: Using sides

Volume Formula Used for Cube => side³ => side * side * side

Formula 2: Using the diagonal of a cube

The volume of a cube can also be determined if you know the length of its diagonal.

Volume Formula Used for Cube => √3 × d³/9

Where d represents the 'diagonal of the cube'

Formula Explanation: Since all of the sides of a cube are of equal length, it is effortless to determine the formula for the volume of a cube. We know that the volume of an object is calculated by the total space any object occupies. With a cube, all the 3-dimensions, i.e. length, breadth, and height, are equal, so it is the multiplication of three sides (side x side x side).

Examples

Example 1: Find the volume of a cube whose length is 6cm each

Solution: According to the cube volume formula:

Volume = (side)³

= (6 cm)³ => 6cm x 6cm x 6cm

= 216 cm³

Example 2: Find the volume of a cube whose diagonal is 3√3 cm

Solution: According to the cube diagonal volume formula:

Volume = √3 × d³/9

= √3 × (3√3 cm)³/ 9

= √3 ×(3√3 × 3√3 × 3√3)/ 9

= √3 × 81√3 / 9

= (√3 × √3) × 81 / 9

= 3 x 81 / 9

= 243 / 9

= 27 cm³

2. Calculating the Volume of a Cuboid

A cuboid is defined as a solid 3-D (three-dimensional) object that consists of six rectangular faces where the opposite faces are identical. Therefore, a cuboid exists as a pair of 3 parallel sides. We know that volume is determined based on three-dimensional sides, i.e. length, width and height. The other name of a cuboid is "Solid Rectangle", as it comprises rectangular faces. All the angles of a cuboid are at right angles, and the opposite sides of a cuboid are identical. An example of the cuboid is a matchbox.

Note: A cube is said as a special rectangular cuboid wherein all the rectangles faces are equal.

Formula

Volume Formula Used for Cuboid => length x width x height=> l x b x h

Formula Explanation: We know that volume of an object is calculated by the total space any object occupies. Therefore, in the case of cuboid, the volume is determined by multiplying the dimensions of these faces, i.e. length, width and height.

Example

Example 1: Determine the capacity of a cuboid tank that has a length of 15 cm, breadth of 8 cm and a height of 9 cm.

Solution: Capacity of cuboid tank = capacity of the cuboid tank

Volume of cuboid = length × width × height

= 15cm × 8cm × 9cm = 1080 cm³

Therefore, the cuboidal tank has a capacity of 1080 cm³.

3. Calculating the Volume of a Cylinder

A cylinder is defined as a 3-D (three-dimensional) solid object that consists of two circular identical flat ends and one curved side that connects both ends. To calculate the volume of a cylinder, one must know the height and radius (the distance between the edge of the circle and its centre point) of one of the flat ends. If the dimensions are given in cm, the volume is measured cubic cm (cm3). Though you can also measure the volume in in3, m3, ft3, etc.

Formula

Volume Formula of Cylinder: V = πr²h

Where

'V' represents the Volume of cylinder

'r' represents radius of the circular cylindrical base

'h' represents the height

'π' represents the constant pi (22/7 or round pi to 3.14)

Formula Explanation:

To calculate the volume of a cylinder one must know its height and radius (the distance between the edge of the circle and its center point) of one of the flat ends.

Example:

Example 1: Determine the volume of a cylindrical roof, which comprises a radius of 7m and height of 21m.

Solution: As per the formula, we know

Volume of a cylindrical = πr²h

Where r= 7m and h = 21m

Putting the values of r and h in our formula

Volume = 3.14 x 7² x 21

= 3.14 x 7 x 7 x 21

= 3231.06 m³

4. Volume of a Regular Square Pyramid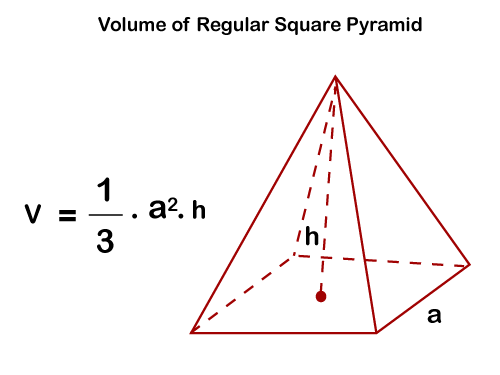

A pyramid is defined as a 3-D (three-dimensional) solid object that consists of a base and adjacent faces that taper at an apex (the point of the pyramid). A right square pyramid is a pyramidal shape in which the base has a right square base, and all the four triangular faces are of equal length, and they are joined at a vertex.

Formula:

Volume of a regular pyramid = 1/3b²h,

Where

'b' represents the of the regular the pyramid (the polygon at the bottom)

'h' represents the height of the pyramid (vertical distance from the base to top).

Example

Question 1: Calculate the volume of the right square pyramid that has a height of 10 cm and base of 5 cm.

Solution: As per the formula, we know.

Then, the volume of the right square pyramid is V = 1/3 × b² × h

⇒ V = 1/3 × 5² × 10
⇒ V = 1/3 × 25x 10
⇒ V = 250/3 = 83.34 cubic cm

The volume of the right square pyramid is ;83.34 cm³.

5. Calculate volume of Sphere

The sphere is defined as the circular 3-D (three-dimensional) solid object wherein every point on its edge is equal to the circle's center. The fixed distance from the center to its edge is called the sphere's radius (R).

Formula

Volume of Sphere (V): 4/3πR³

where

'V' represents the Volume of sphere

'r' represents radius of the sphere fixed distance

'π' represents the constant pi (22/7 or round pi to 3.14)

Examples

Question.1: Determine the volume of a spherical ball that has a radius of 6cm?

Solution: As per the Sphere volume formula, we know

Volume of a sphere = 4/3 πr³,

where r= 6cm

putting the value of r in our formula

V = 4/3 x 3.14 x 6³

V = 4/3 x 3.14 x 6 x 6 x 6

V = 904.32 cm³

Q.2: Calculate the volume of a solid sphere where the diameter is equal to 8m.

Solution: Given, diameter = 8 cm

So, radius = diameter/2 = 8/2 = 4 cm

As per the formula, the volume of sphere is;

Volume = 4/3 πr³ cubic units

V = 4/3 π 4³

V = 4/3 x 3.14 x 4 x 4 x 4

V = 4/3 x 3.14 x 64

V = 267.94 cm³.

Measuring the volume of irregular solids

In the above part, we discovered how to calculate the volume of solid objects, but what about objects of irregular shape as shown in the below image.

For regular 3-D figures, one can easily find their respective volume by measuring their dimensions and using the suitable volume formula. However, if you want to calculate the volume of an irregular shape, you need to apply the Archimedes formula.

Fun Fact: Do you show that Archimedes came up with the entire volume theory while taking a bath. One day when he was stepping into a bathtub, he suddenly observed that the tub's water level rose as he put his body inside.

Conclusion:

From the above observation, Archimedes concluded that the volume of water displaced in any container is equal to the volume of the object immersed in it.

So, if you want to calculate the volume of an irregular object, follow the below-given steps that are based on Archimedes principle:

Take a container (beaker, bucket, measuring cup or graduated cylinder) and an irregular object for which you want to calculate the volume. Ensure that the container's size should be bigger than the object so it can be submerged easily, and the container should have a scale.
The next step is to pour water into the container and measure the volume with the help of its scale.
After that, immerse your irregular object inside the container. Make sure it should be entirely dipped inside the water to get the accurate volume. The water level will rise, read off the measurements.

Note: Archimedes principle will not work if your irregular object dissolves in water.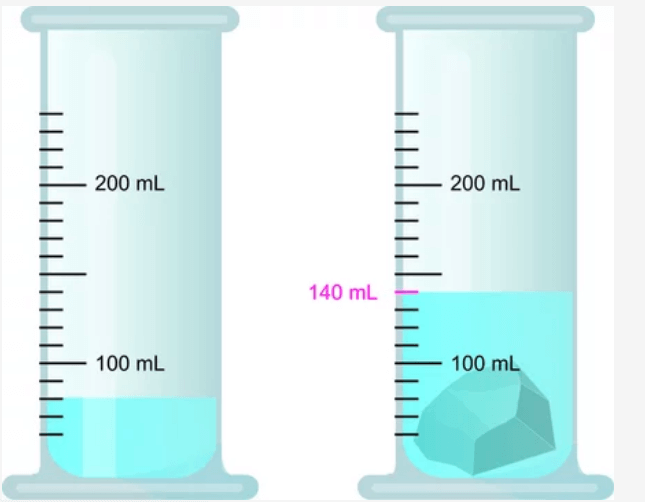

The above scale measurements are essential for determining the buoyancy force built on Archimedes' principle.
Calculate the volume of the container before and after immersing the irregular stone in it. The difference between both the container volumes will be the actual volume of our irregular object.

Next TopicWhat's a URL

← prev next →