How to find Area of a Circle

In this section, we will learn how to find the area of a circle. At the last of this section, we have explained some examples related to the area of a circle with different scenario for better understanding.

Circle: A circle can be defined as a locus (a set of points in a particular position) of points that maintain equidistant from another point called the center. In other words, a circle is a geometrical shape whose distance from the center to the edge is always the same. Every circle has a center.

A circle has the following components:

• Origin: It is a point that lies exactly at the center of a circle is called the origin. It is denoted by o.
  
• Radius: The distance from the radius to circumference is called the radius. In other words, it is half of the diameter. It is denoted by r.
  r=d/2
  
• Diameter: It is the length of a line that splits a circle into two equal parts is called the diameter. The line should be passed through the center. In other words, the diameter is twice the radius of a circle. It is denoted by d.
  d = 2r
  
• Chord: The line whose endpoints lie on the circle is called a chord. In other words, it is a line that joins two points on any curve. Every diameter is a chord. But not every chord is a diameter. In the following figure, the line segment AB is a chord.
  
• Circumference: The reign covered by the circle is called the circumference. It is denoted by C.
  C = πd       or     C = 2πr
  Where π is a constant whose value is 3.1415.
  

Definition

The reign occupied by a circle in the 2D plane is called the area of a circle. In other words, all the space covered by the circle's circumference is called the area of a circle.

In the following figure, the colored area represents the area of the circle.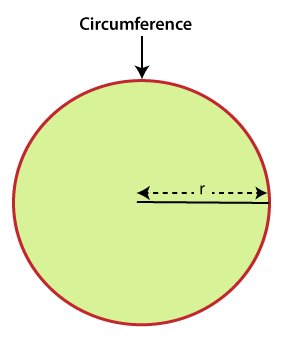

Area of Circle Formula

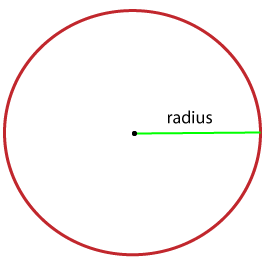
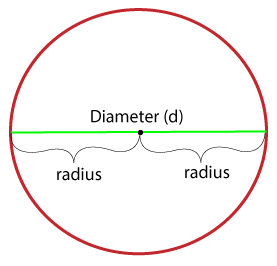
Where,

A: represents the area of a circle.

π: is a constant whose value is 3.1415 or 22/7.

r: represents the radius of a circle

Derivation of Area of Circle

There are two methods for deriving the area of circle formula:

• Using rectangles
• Using triangles

Using Rectangles

Draw a circle and divide it into 16 equal parts. For better understanding, we have filled two colors (red and green) in these parts. as we have shown in figure(a). After dividing, each part of the circle represents a triangle. Arranged these triangles, as we have shown in the figure(b). The resultant figure forms a parallelogram-shaped.

The area of parallelogram-shaped will be equal to the area of a circle because each part has the same area and equal arc length.

The green color parts represent half of the circumference, and the other part in red color represents the other half circumference.

If the number of parts increased, the parallelogram-shape looks like a rectangle whose length is equal to πr and breadth is equal to r.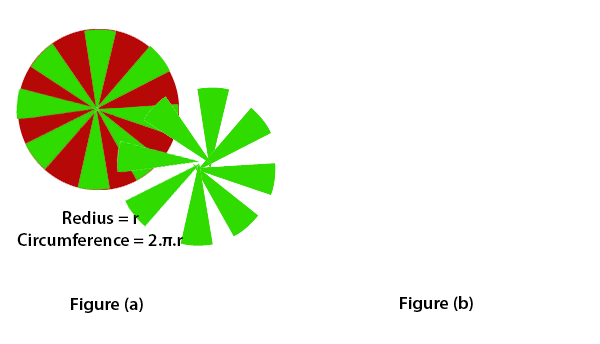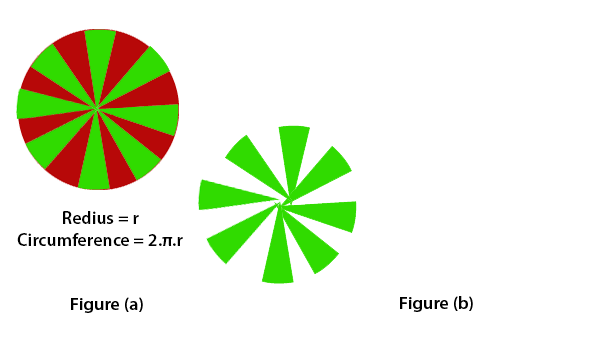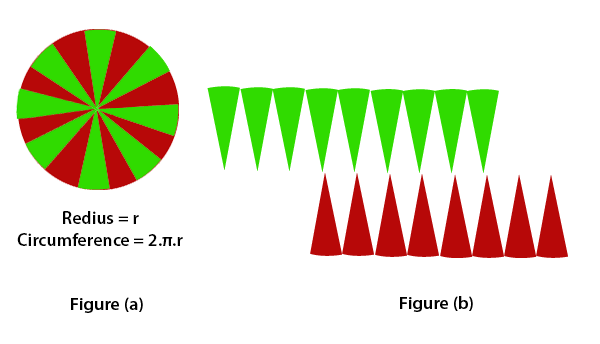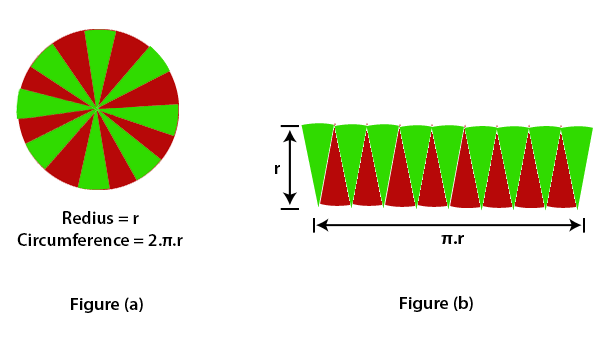

We know that,

The area of a rectangle (A) = w * l

Where w is the width, and l is the length of the rectangle.

From the figure,

width (w) = πr and length (l) = r

putting these values in the formula, we get area (A) = πr * r

Hence,

Using Triangle

Draw a circle with radius r. In this circle, draw some other concentric circles (the circle that has the same center), as shown in figure (a). Now cut the circle up to the center and spread it. The resultant shape will be a triangle, as we have shown in the figure (b).

The base and height of the triangle will be equal to the circumference and radius of the circle, respectively.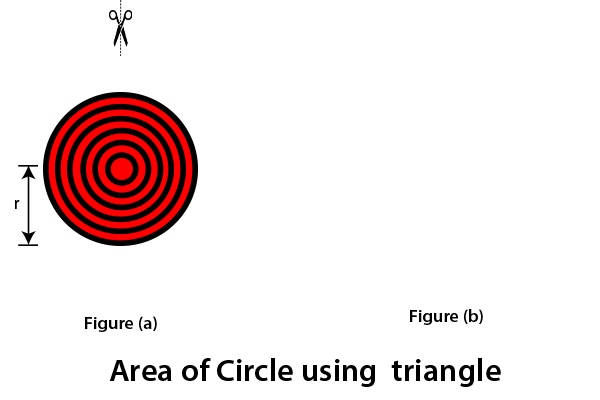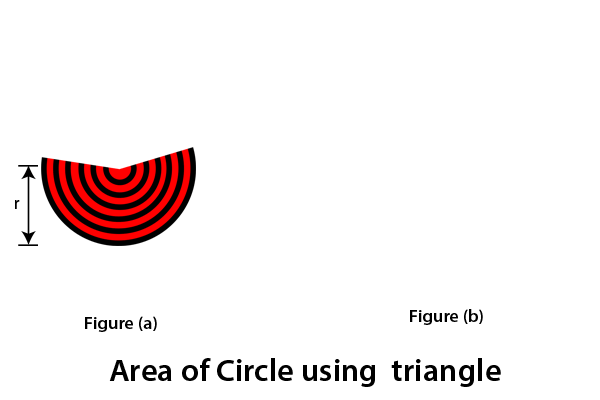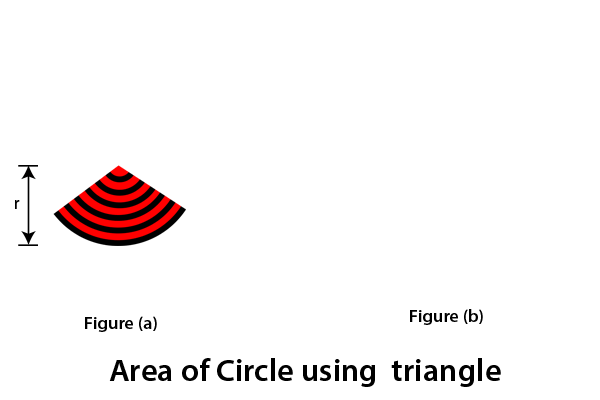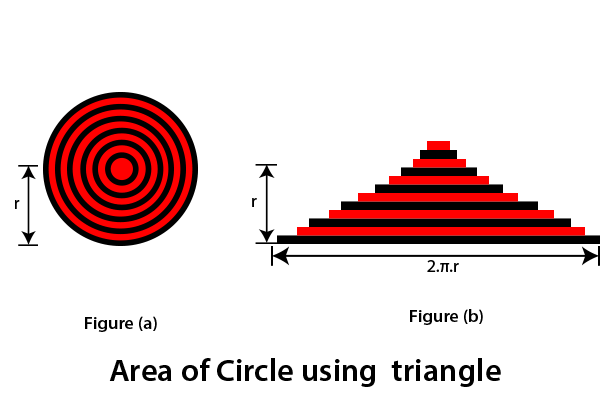

When we calculate the area of a triangle, it gives the area of a circle as a result.

We know that:

Area of triangle (A) = ½*base*height

From the above figure,

base = 2πr and height= r

Put the value of base and height in the area of triangle formula,

Hence,

Examples

When the diameter is known

Example 1: Find the area of a circle if the diameter of a circle is 15 cm.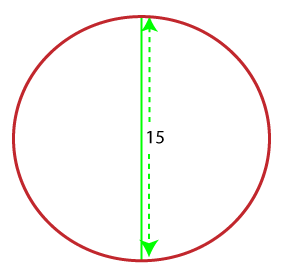

Solution:

We have given, diameter (d) = 15 cm.

Area =?

First, we will find the radius.

We know that,

d = 2r

From the above formula,

We know that,

When the radius is known

Example 2: Find the area of a circle if the radius of a circle is 10 cm.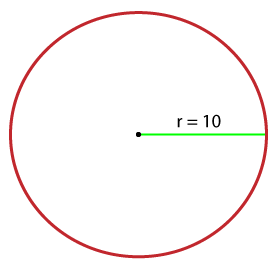

Solution:

We have given, radius (r) = 10 cm.

Area =?

We know that,

area of circle (A) = πr²

putting the value of r in the above formula,

A = 314.00 sq cm.

When circumference is known

Example 3: Find the area of a circle if the circumference of a circle is 20 cm.

Solution:

Given, circumference (C) = 20 cm

Area =?

We know that,

Circumference (C) = 2πr

From the above formula,

we know that,

area of circle (A) = πr²

A = 3.14 * (31.40 * 31.40)

A = 3.14 * 985.96

A = 3095.9144 sq cm.