How to find Chromatic Number | Graph coloring AlgorithmTo understand this example, we have to know about the previous article, i.e., Chromatic Number of Graph in Discrete mathematics. In the section of Chromatic Numbers, we have learned the following things:
Graph Coloring Algorithm
However, we can find the chromatic number of the graph with the help of following greedy algorithm. Greedy AlgorithmThere are various steps to solve the greedy algorithm, which are described as follows: Step 1: In the first step, we will color the first vertex with first color. Step 2: Now, we will one by one consider all the remaining vertices (V -1) and do the following:
Disadvantages of Greedy Algorithm The greedy algorithm contains a lot of drawbacks, which are described as follows:
Examples of finding Chromatic number of a GraphThere are a lot of examples to find out the chromatic number in a graph. Some of them are described as follows: Example 1: In this example, we have a graph, and we have to determine the chromatic number of this graph. 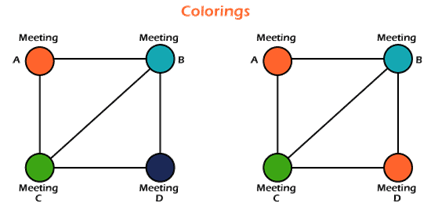
Solution: When we apply the greedy algorithm, we will have the following:
From the above table,
So with the help of 2 colors, the above graph can be properly colored like this: 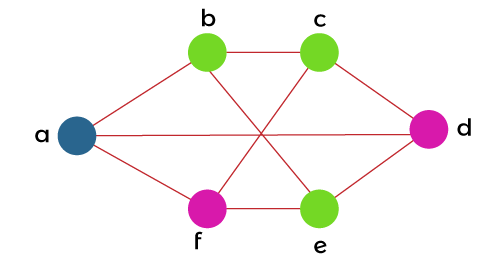
Example 2: In this example, we have a graph, and we have to determine the chromatic number of this graph. 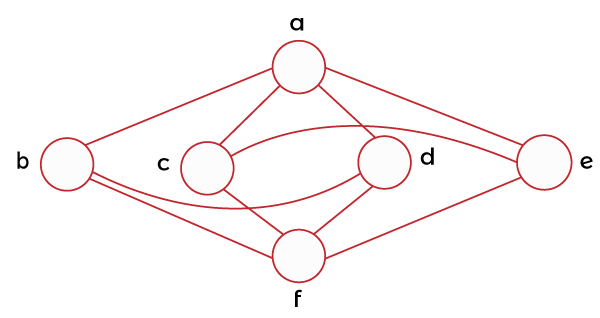
Solution: When we apply the greedy algorithm, we will have the following:
From the above table,
So with the help of 3 colors, the above graph can be properly colored like this: 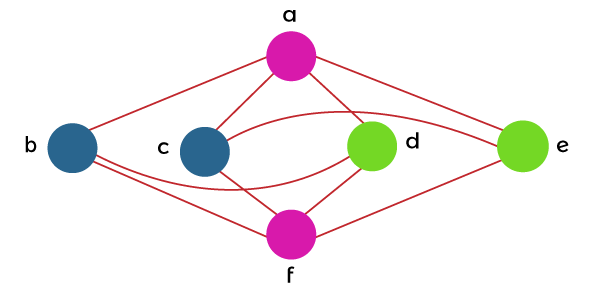
Example 3: In this example, we have a graph, and we have to determine the chromatic number of this graph. 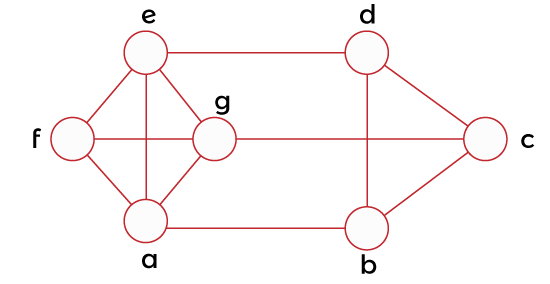
Solution: When we apply the greedy algorithm, we will have the following:
From the above table,
So with the help of 4 colors, the above graph can be properly colored like this: 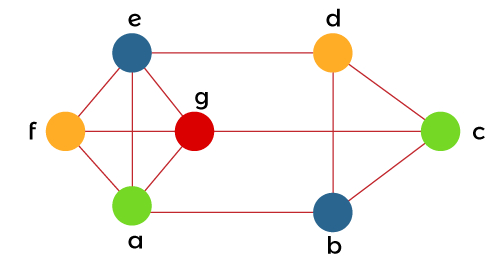
Example 4: In this example, we have a graph, and we have to determine the chromatic number of this graph. 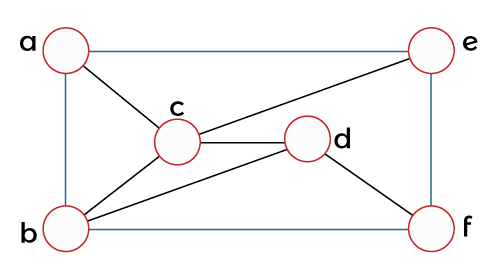
Solution: When we apply the greedy algorithm, we will have the following:
From the above table,
So with the help of 3 colors, the above graph can be properly colored like this: 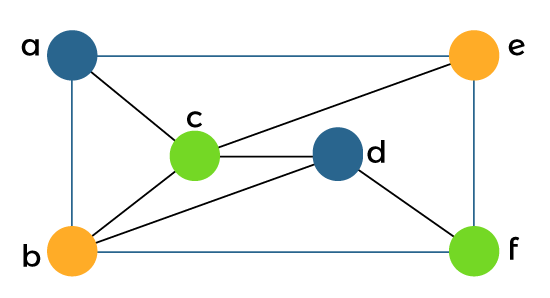
Example 5: In this example, we have a graph, and we have to determine the chromatic number of this graph. 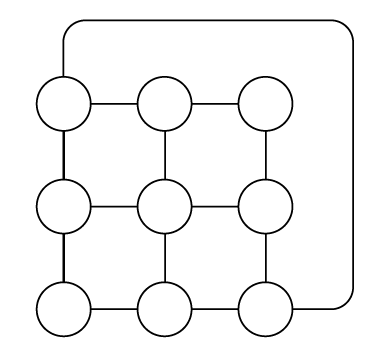
Solution: When we apply the greedy algorithm, we will have the following:
So with the help of 3 colors, the above graph can be properly colored like this: 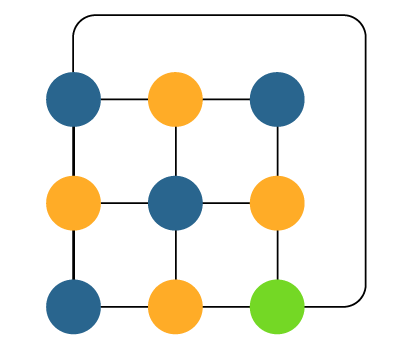
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










