How to Find SlopeIn mathematics, the line is implemented everywhere, such as geometry, algebra, etc. The slope defines the direction and steep of the line. If we know the concepts related to the line, it will be easy for us to understand the other concepts where the line is implemented. In this section, we will learn slope definition, slope formula, types of slope, and how to find the slope of a line, along with the proper examples. Slope DefinitionThe slope defines the steepness of the line. The word steepness means how much the line is slanted. In other words, the slope shows the direction of a line on the coordinate plane. It is also known as the gradient of a line. The real-life example of the slope is a ramp, stairs, and sliding swing, etc. 
Slope FormulaWe can calculate the slope of a line by dividing the change in height (∆y) by change in horizontal distance (∆x). The slope is denoted by m. 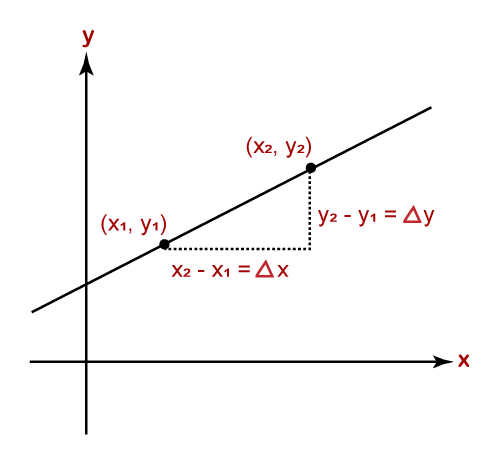

Where: m: is slope (x1,y1): coordinates of first point in the line (x2,y2): coordinates of second point in the line y2-y1=∆y: means vertical change x2-x1=∆x: means horizontal change We can also write the above formula as: 
Rise: The vertical change in a line is known as the rise or fall. Run: The horizontal change in a line is known as the run. 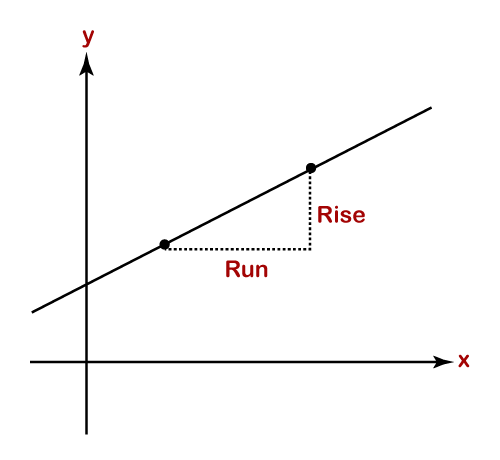
Types of the SlopeTypes of slope also known as the direction of slopes because it shows the direction of a line. There are four types of slope:
Positive Slope: In the positive slope, two variables x and y positively related to each other. It means when x increases, the point y also increases. When y decreases, the point x also decreases. The positive slope moves left to right in the upward direction. 
In the following graph, the line is moving from left to right in the upward direction that denotes the positive slope. 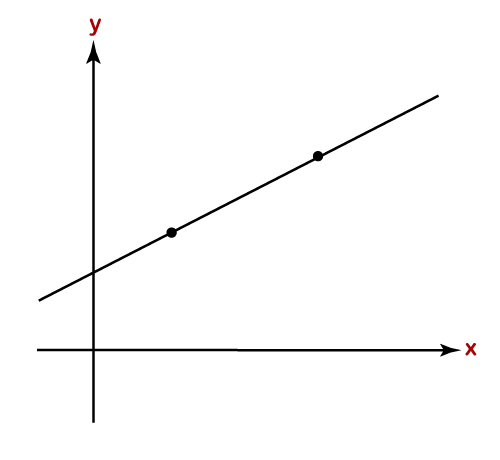
Negative Slope: In the negative slope, two variables x and y negatively related to each other. It means when x increases, the point y decreases. When x decreases, the point y increases. The negative slope moves left to right in the downward direction. The slope will be negative if m<0. 
In the following graph, the line is moving from left to right in the downward direction that denotes the negative slope. 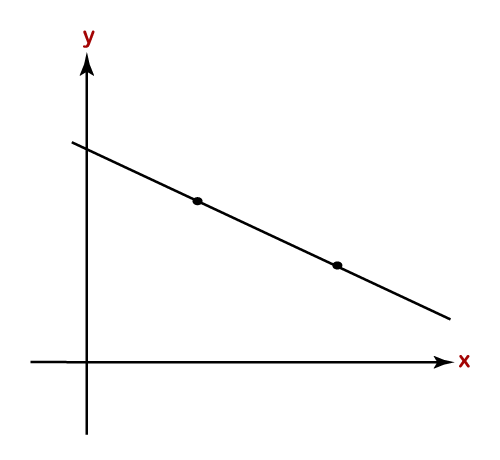
Zero Slope: In the zero slope, the line is parallel to the x-axis, and y-coordinate never changes. The value of is 0. It is the slope of the horizontal line. 
In the following graph, the line is parallel to the x-axis that denotes the zero slope, and y remains the same, no matter what the x is. 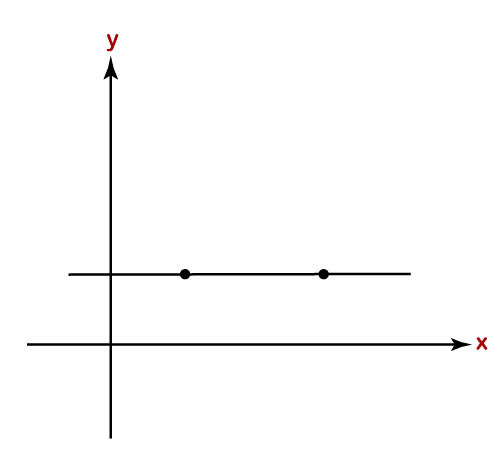
Undefined Slope: In the undefined slope, the line is parallel to the y-axis and the value of ∆x is 0. It is the slope of the vertical line. The x-coordinate never changes no matter what the y-coordinate is. It is the opposite of zero slope. 
In the following graph, the line is parallel to the y-axis that denotes the undefined slope. 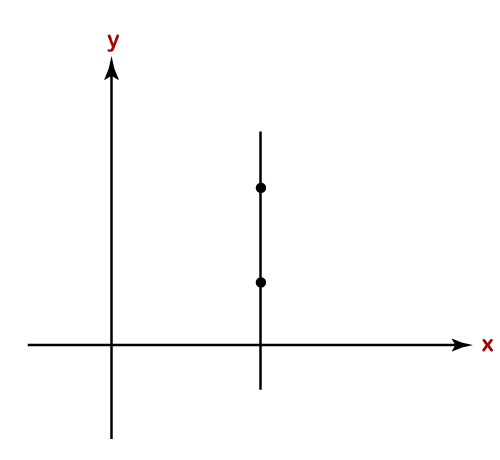
From the above definitions, we can conclude that:
How to Find SlopeLet's solve some examples based on the slope. Example 1: Find the slope of the line given below. 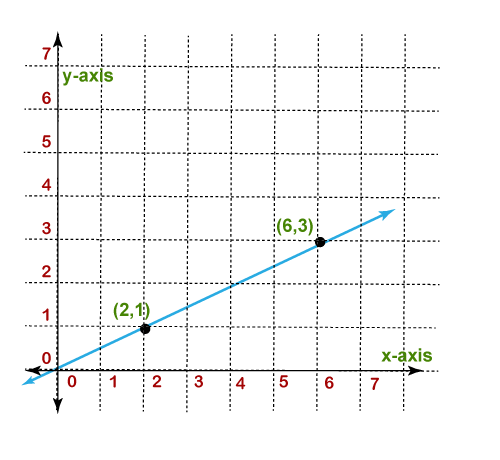
Solution: From the above figure, (x1,y1)=(2,1) and (x2,y2)=(6,3) According to the formula: 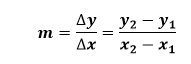
Putting the values in the above formula, we get: 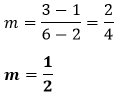
The value of m is positive, so it denotes the positive slope. Hence, the slope of the given line is Example 2: Find the slope of the line if the two points on the line are (0, 2) and (-2, 6). Also, draw the line on the graph. Solution: Given, the coordinate of the line is (x1,y1)=(0,2) and (x2,y2)=(-2,6) According to the formula: 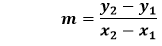
Putting the values in the above formula, we get: 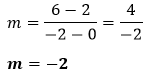
The value of m is negative, so the line denotes the negative slope. Hence, the slope of the line is -2. 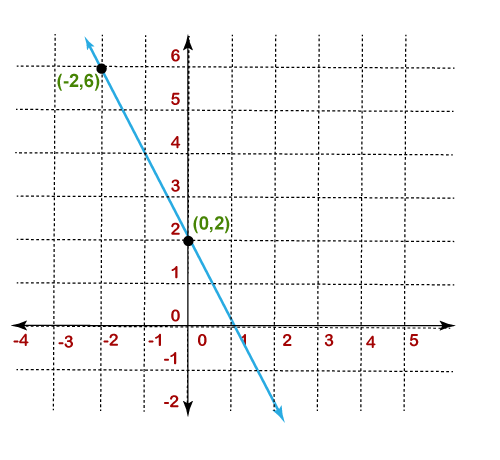
Example 3: What is the slope of the line that contains the points (4, 2) and (0, 2). Draw the graph, and also find that slope is positive or negative or horizontal or vertical. Solution: Given, the coordinate of the line is (x1,y1)=(4,2) and (x2,y2)=(0,2) According to the formula: 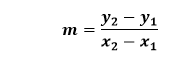
Putting the values in the above formula, we get: 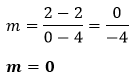
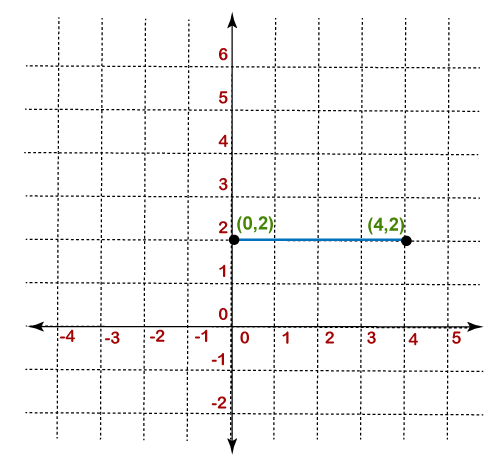
The value of m is zero, so the line is horizontal and y never change. Hence, the slope of the line is -2. Example 4: A line has coordinates (2, 4) and (2, -2). Find the slope of the line. Solution: Given, the coordinate of the line is (x1,y1)=(2,4) and (x2,y2)=(2,-2) According to the formula: 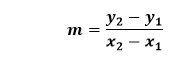
Putting the values in the above formula, we get: 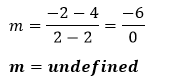
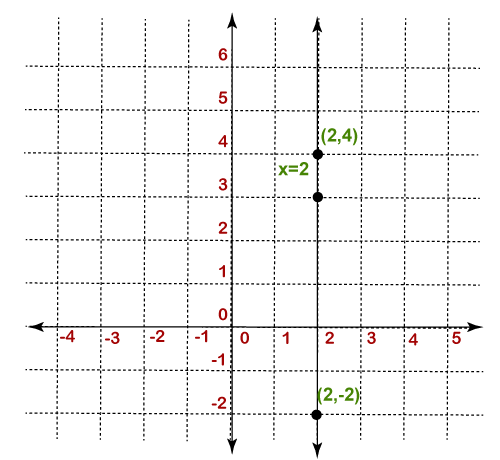
The value of m is undefined, so the line is vertical and x never change. Hence, the slope of the line is undefined. Example 5: If the rise of a line is 4.8 and run is 6.2. Find the slope of the line. Solution: Given, rise=4.8 and run=6.2 According to the formula: 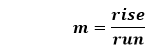
Putting the values in the above formula, we get: 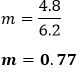
Hence, the slope of the line is 0.77. Example 6: Find the slope of the line given below. 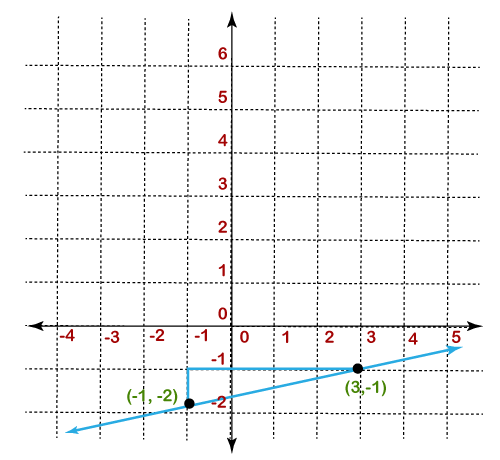
Solution: Given, the coordinate of the line is (x1,y1)=(-1,-2) and (x2,y2)=(3,-1) According to the formula: 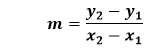
Putting the values in the above formula, we get: 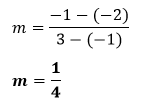
Hence, the slope of the line is Example 7: The equation of a line is y= Solution: The given equation is y= We know that, the equation of line is y=mx+b. Comparing the equations, we get: m= Hence, the slope of line is
Next TopicTrapezoid Parallel Sides
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





 .
.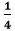
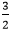 x-6. Find the slope of the line.
x-6. Find the slope of the line.




