Improper Fraction Definition

History

The history of fractions is very vast and important; let us discuss this in brief. The word 'Fraction' evolved from the Latin word 'Fractio', which simply means 'to break'. We have to go back in time to understand the history of fractions (metamorphically). In 1800, the Egyptians were trying to write numbers by figures and notations, so they wrote fractions using what we call 'unit fraction', which means 1 as the numerator. They used to put a picture of mouth (which means fraction in their language) above the notation of their numbers to denote a unit fraction. However, this was not effective for large numbers.

Then Babylonians tried to represent a fraction in their own language, they tried to do this in the Roman method, but they only used two symbols. Therefore, it was not effective to use.

Around 500AD, the Indians represented numbers using ' Brahmi', which was the representation of numbers from 0 to 9. The Indians used to represent a fraction, as we do now, but without the bar between them.

For example: 3

2

It was Arabs who added that line in between those numbers, which we use today. Before talking about improper fractions, let us discuss fractions.

Fraction:

A fraction can be defined as a part of a whole that whole can be any number, thing, quantity, etc. Basically, a fraction is a real number between two integers. A fraction contains the top part and bottom part, the top part represents the number of things or part chosen from the whole thing or object, and the bottom part represent the whole thing or object. Let us take an example of a circle and divide that circle into five equal parts (as shown in the image). To represent a single part of that circle, we have to write 1/5 th part of the whole circle, i.e., 1/5 in this 1 represents the part that we have selected, and 5 represents the whole circle that has been divided into five equal parts.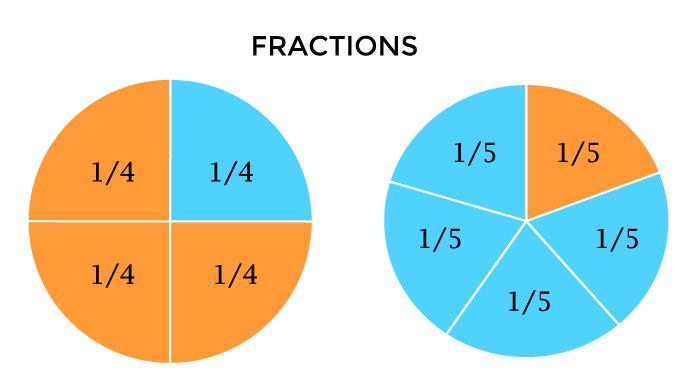

Parts of a Fraction

A fraction consists of mainly two parts, top and bottom, known as

1. Numerator
2. Denominator

1. Numerator: A Numerator is the top part of a fraction that represents the number or numbers of parts you have selected from a whole thing.

2. Denominator: A Denominator is the bottom part of a fraction; that number shows us that in how many parts we have divided the whole thing or object.

Let's take an example of 1/5, as mentioned above.

Here, 1 is the numerator, and 5 is the denomination, which shows we are representing 1 part of a circle that is divided into five parts.

Fraction on the Number line

As we stated before, a fraction is a number between two integers. Let us discuss this in brief by taking examples of 1/5 and 3/5. To represent these numbers on a number line, follow the given steps.

Step1. Select the interval in which we want to represent these numbers, let us say 0 to 1.

Step2. Now see the denominator of the given number, i.e., 5. So divide the number line into five parts in the interval 0 to 1, as shown in the image.

Step3. Now see the numerator of the given number, i.e., 1 and 3. So in increasing order from 1 to 5 in intervals 0 to 1, we represent the numbers 1/5 and 3/5 as shown in the image.

Types of a Fraction

On the bases of the numerical values of the numerator and denominator, there are mainly three types of fraction

1. Proper Fraction
2. Improper Fraction
3. Mixed Fraction

1. Proper Fraction: A Proper Fraction can be defined as a fraction in which the value of the numerator is comparatively less than the value of the denominator, i.e., numerator < denominator.

Let's take an example of 3/7

Here, 3 is clearly less than 7, 3 < 7.

So 3/7 is a Proper Fraction.

2. Improper Fraction: An Improper Fraction can be defined as a fraction in which the value of the numerator is comparatively greater than the value of the denominator, i.e., numerator > denominator.

Let us take an example of 9/7

Here, 9 is greater than 7, 9 > 7.

Therefore, 9/7 is an Improper Fraction.

3. Mixed Fraction: A Mixed Fraction can be defined as a fraction that is a combination of an integer and a proper fraction. A Mixed fraction has a special representation.

For Example: 2(3/4) is expressed as 2 whole 3 by 4.

Here, we are talking about Improper Fraction.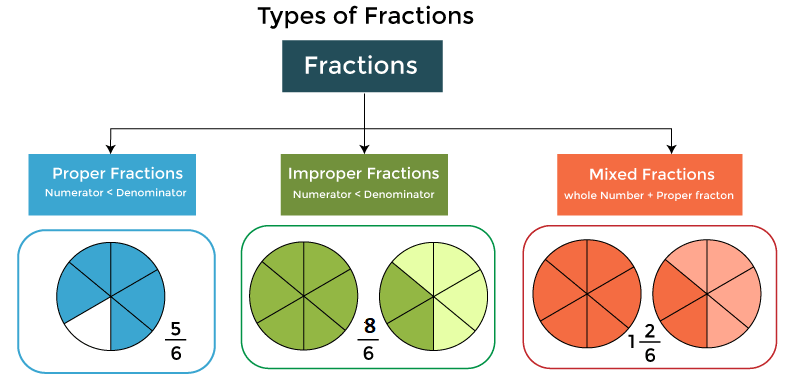

Definition of Improper Fraction:

In terms of mathematics, an improper fraction is a Rational Number, a Rational Number is a number that can be represented as a fraction of two integers in which the value of the denominator can never be equal to zero, whose absolute value can be greater than 1 or equal to 1, an improper fraction can be positive and negative.

For example, -3/2 and 7/5 are improper fractions.

Adding Improper Fraction (Fraction)

We can divide the addition of the improper fraction into two parts

1. When the denominators of fractions are the same.
2. When the denominators of fractions are different.

When the denominators of fractions are the same: It is easy to solve this type of addition when the denominators of fractions are the same.

Let's take 7/3, 4/3 as examples; adding these numbers (improper fractions)

7/3 + 4/3 = 11/3

When the denominators of fractions are different: It is also quite easy to solve when we know the right way to do this; let's learn that way by following the steps given below.

Step1. In this step, we will take the denominators and find the LCM (Least Common Multiple) of the denominators.

Step2. In this step, we will divide the LCM with the denominators and remember those numbers.

Step3. In this step, we will multiply and add (respectively) the numerators with those numbers that we calculated in Step 2.

Step4. After adding those numbers and putting LCM as the denominator, we will get our result.

Let's follow these steps and find the addition of 5/2 and 4/3.

Step1. Taking LCM of 2 and 3, as 2 and 3 are the denominators of the given fraction, i.e., LCM (2, 3) = 6.

Step2. Dividing 6 by 2 and 3, we will get 3 and 2, respectively.

Step3. Multiplying 5 with 3 and 4 with 2 and adding both of them.

Step4. Adding 15 and 8 and putting 6 as the denominator, we will get 23/6 as our result.

5/2 + 4/3 = {(5 * 3) + (4 * 2)} / LCM (2, 3) = {(15) + (8)} / 6 = 23 / 6 answer.

Multiplying Improper Fractions

Multiplying improper fractions is quite simple; we just have to multiply numerator to numerator and denominators to denominators.

Let's take an example of multiplying 3/2 and 7/4.

(3 / 2) * (7 / 4) = {3 * 7} / {2 * 4} = 21 / 8

Subtracting Improper Fractions

We can divide the subtraction of the improper fraction into two parts

1. When the denominators of fractions are the same.
2. When the denominators of fractions are different.

When the denominators of fractions are the same: It is easy to solve this type of subtraction when the denominators of fractions are the same.

Let's take 7/3, 5/3 as examples; subtracting 5/3 from 7/3.

7/3 - 5/3 = 2/3

2. When the denominators of fractions are different: It is also quite easy to solve when we know the right way to do this; let us learn that way by following the steps below.

Step1. In this step, we will take the denominators and find the LCM (Least Common Multiple) of the denominators.

Step2. In this step, we will divide the LCM with the denominators and remember those numbers.

Step3. In this step, we will multiply and subtract (respectively) the numerators with those numbers that we calculated in Step 2.

Step4. After subtracting those numbers and putting LCM as the denominator, we will get our result.

Let us follow these steps and find the subtraction 4/3 from 5/2.

Step1. Taking LCM of 2 and 3, as 2 and 3 are the denominators of the given fraction, i.e., LCM (2, 3) = 6.

Step2. Dividing 6 by 2 and 3, we will get 3 and 2, respectively.

Step3. Multiplying 5 with 3 and 4 with 2 and adding both of them.

Step4. Subtract 8 from 15 and put 6 as the denominator; we will get 9/6 can also be written as 3/2.

5/2 - 4/3 = {(5 * 3) - (4 * 2)} / LCM (2, 3) = {(15) - (8)} / 6 = 9 / 6 = 3 / 2 answer.

Dividing Improper Fractions (Fractions)

Dividing improper fractions is quite simple; just multiplying the reciprocal, changing the position of the numerator and denominator with each other is called reciprocal, of the other fraction by which we have to divide the first fraction.

Let's take the example of dividing 3/2 by 8/5.

(3/2) / (8/5) = (3/2) * (5/8) = (3 * 5) / (2 * 8) = 15 / 16 answer.

Properties of Improper Fraction

1. On solving an Improper Fraction, the obtained value will always be greater than (>) or equal to 1.
2. Improper fractions can be converted to mixed fractions, and a mixed fraction can be converted back to an improper fraction.
3. In an improper fraction, the numerator of a fraction will always be greater than or equal to the denominator of that fraction.
4. In an improper fraction, the denominator of a fraction will always be a positive integer.

Applying some properties of the Real number on Improper Fractions

1. Commutative property: This property states that; the result will not change whether the order of the terms (fractions) changes while adding and multiplying the terms (fractions), i.e., x + y = y + x and x * y = y * x.

For example: (a.) Let's take an example of (5/2) and (3/2) on applying addition.

5/2 + 3/2 = 8/2 = 4

(b.) Let's take an example of (5/4) and (3/2) on applying multiplication.

(5/4) * (3/2) = (5*3) / (4*2) = 15/8

2. Associative property: This property states that; the result will not change whether the grouping of the terms (fractions) changes while adding and multiplying the terms (fractions), i.e., x + (y + z) = (x + y) + z and x * (y * z) = (x * y) * z.

For example: (a.) Let's take an example of (5/2), (3/2) and (7/2) on applying addition. 5/2 + 3/2 + 7/2 = 15/2

(b.) Let's take an example of (5/2), (3/2) and (7/2) on applying multiplication.

(5/2) * (3/2) * (7/2) = (5 * 3 * 7) / (2 * 2 * 2) = 105/8

3. Distributive property: This property states that; multiplying a sum by a number is the same as multiplying each term in the sum by that number and then adding the results, i.e., x * (y + z) = x*y + x*z.

For example: Let us take an example of (5/2), (3/2) and (7/2).

L.H.S. (5/2) * (3/2 + 7/2) = (5/2) * (10/2) = 25/2

R.H.S. (5/2 * 3/2) + (5/2 * 7/2) = (15/4) + (35/4) = 50/4 = 25/2

4. Identity property: This property states that there exists an element (fraction) for every element (fraction) such that adding and multiplying that element (fraction) to the given element (fraction) results in the element itself, i.e., x + 0 = x and x * 1 = x.

Here, zero (0) is the additive identity of any number or fraction and one (1) is the multiplicative identity of any number or fraction.

For example: Let us take 7/5

7/5 + 0 = 7/5 and (7/5) * 1 = 7/5

5. Inverse property: This property states that there exists an element (fraction) for every element or fraction such that adding and multiplying that element or fraction to the given element or fraction gives additive identity and multiplicative identity, respectively, i.e., x + (- x) = 0 and x * (1/x) = 1.

For example: Let us take 5/3

5/3 + (- 5/3) = 0 and (5/3) * (3/5) = 1

Here, -5/3 is the additive inverse fraction of the fraction 5/3 and 3/5 is the multiplicative inverse of the fraction 5/3.

6. Closer property: This property states that when we add, multiply, subtract, and divide two fractions, the resultant is also a fraction.

For example: Let us consider 5/3

• 5/3 + 5/3 = 10/3, 10/3 is also a fraction.
• (5/3) * (5/3) = 25/9, 25/9 is also a fraction.
• 5/3 - 5/3 = 0, 0 is also a fraction as it can be written as 0/1.
• (5/3) / (5/3) = 1, 1 is also a fraction as it can also be written as 1/1.

Application of the Improper Fractions

1. Measurements: Improper fractions are used in many different types of measurements, such as length, weight, and time. For example, if a recipe calls for 1 and 1/2 cups of flour, this can be expressed as the improper fraction 3/2 cups.
2. Finance: Improper fractions are used in finance to calculate interest rates, mortgages, and loans. For example, a mortgage payment may be calculated using an improper fraction to represent the interest rate.
3. Engineering: Improper fractions are used in engineering to represent ratios of different components in a system. For example, the compression ratio of an engine can be expressed as an improper fraction.
4. Probability: Improper fractions are used in probability to represent the likelihood of an event occurring. For example, if there are 8 red marbles and 4 green marbles in a bag, the probability of picking a red marble can be expressed as the improper fraction 8/12.
5. Geometry: Improper fractions are used in geometry to represent ratios of different dimensions. For example, the ratio of the circumference of a circle to its diameter is an improper fraction, which is commonly represented as pi.
6. Algebra: Improper fractions are used in algebra to solve equations and inequalities that involve fractions. For example, if an equation involves an unknown fraction, the first step may be to convert the improper fraction to a mixed number.
7. Data Analysis: Improper fractions are used in data analysis to represent percentages and proportions. For example, if 75% of the students in a class are female, this can be expressed as the improper fraction 3/4.
8. Computer Science: Improper fractions are used in computer science to represent decimal numbers in binary or hexadecimal notation. For example, the decimal number 10.5 can be expressed as the improper fraction 21/2 in binary notation.