Injective Function in Discrete mathematics

The injective function is also known as the one-to-one function. With the help of injective function, we show the mapping of two sets. In this mapping, we will have two sets, f and g. One set is known as the range, and the other set is known as the domain. The one-to-one function or injective function can be written in the form of 1-1. A function g will be known as one to one function or injective function if every element of the range corresponds to exactly one element of the domain. A function f() is a method that is used to relate the elements of one variable to the elements of a second variable. It happens in a way that elements of values of a second variable can be identically determined by the elements or values of a first variable.

We have various sets of functions except for the one-to-one or injective function to show the relationship between sets, elements, or identities. These functions are described as follows:

1. Bijective function or Onto function
2. Suejective function or Many to one function

Definition of Injective function

The injective function or one-to-one function is the most commonly used function. It can be defined as a function where each element of one set must have a mapping with a unique element of the second set. If there are two sets, set A and set B, then according to the definition, each element of set A must have a unique element on set B. In the injective function, the answer never repeats. The representation of an injective function is described as follows: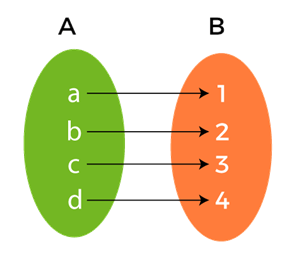

In other words, the injective function can be defined as a function that maps the distinct elements of its domain (A) with the distinct element of its codomain (B). To understand the injective function we will assume a function f whose domain is set A. This function will be known as injective if f(a) = f(b), then a = b for all a and b in A. Same as if a ≠ y, then f(a) ≠ f(b). Formally, we can say that a function f will be one to one mapped if f(a) = f(b) implies a = b.

Similarly, if there is a function f that is injective and contains domain A and range B, then we can find the inverse of this function with the help of following:

Suppose there is a function f: A → B. If the images of distinct elements of A are distinct, then this function will be known injective function or one-to-one function. Otherwise, this function will be known as a many to one function.

Now we will show two images in which the first image shows an injective function and the second one is not an injective function, which means it is many to one.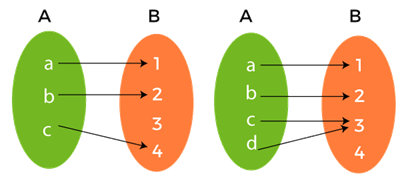

In the above image contains the two sets, Set A and Set B. Set A is used to show the domain and set B is used to show the codomain. In image 1, each and every element of set A is connected with a unique element of set B. Thus, image 1 means the left side image is an injective function or one-to-one function. In the second image, two elements of set A are connected with a single element of set B (c, d are connected with 3). Thus, image 2 means the right side image is many to one function.

Example of injective function:

Injective functions are also shown by the identity function A → A.

Example 1: In this example, we will consider a function f: R → R. Now have to show whether f(a) = 2a is one to one function or an injective function or not.

Solution: Here, R is the real number.

When we put the values of a, we will get

If a = 1, then f(1) = 2

If a = 2, then f(2) = 4

If a = 3, then f(3) = 6

If a = -1, then f(-1) = -2

Hence, each function generates different output for every input. So we can say that the function f(a) = 2a is an injective or one-to-one function.

Example 2: In this example, we will consider a function f: R → R. Now have to show whether f(a) = a/2 is an injective function or not.

Solution: Here, R is the real number.

When we put the values of a, we will get

If a = 1, then f(1) = 0.5

If a = 2, then f(2) = 1

If a = 3, then f(3) = 1.5

If a = 4, then f(-1) = 2

Hence, each function generates a different output for every input. So we can say that the function f(a) = a/2 is an injective function.

Example 3: In this example, we will consider a function f: R → R. Now have to show whether f(a) = a² is an injective function or not.

Solution: Here, R is the real number.

When we put the values of a, we will get

If a = 1, then f(1) = (1)² = 1

If a = 2, then f(2) = (2)²= 4

If a = 3, then f(3) = (3)² = 6

If a = -1, then f(-1) = (-1)²= 1

If a = -2, then f(-2) = (-2)²= 4

Hence, each function does not generate different output for every input. For input -1 and 1, the output is same, i.e., 1. The same happened for inputs 2, -2, and so on. So we can say that the function f(a) = a² is not an injective or one to one function,

Example 4: Suppose a function f: R → R. Now have to show whether f(a) = a³ is one to one function or an injective function.

Solution: Here, R is the real number.

When we put the values of a, we will get

If a = 1, then f(1) = (1)³ = 1

If a = 2, then f(2) = (2)³= 8

If a = 3, then f(3) = (3)³ = 27

If a = -1, then f(-1) = (-1)³= -1

Hence, each function generates a different output for every input. So we can say that the function f(a) = a³ is an injective or one-to-one function.

Injective Graph - Horizontal Line test

With the help of a geometric test or horizontal line test, we can determine the injective function.

1. The function will not map in the form of one-to-one if a graph of the function is intersected by the horizontal line more than once.
2. The function will be mapped in the form of one-to-one if their graph is intersected by the horizontal line only once.

To understand this, we will assume a graph of the function (x) = sin x or cos x, which is described in the following image: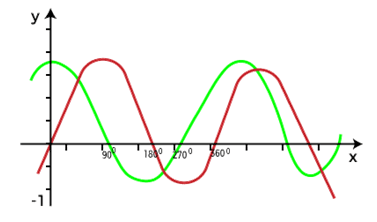

In the above graph, we can see that while drawing a horizontal line, it intersects the graph of cos x and sin x more than once. That's why we can say that these functions are not injective functions or one-to-one functions.

In the below image, we will show the example of one-to-one functions.

In this image, the horizontal line test is satisfied by these functions. That's why these functions are injective.

Is parabola an injective function?

Parabola is not an injective function. We can prove this theory with the help of horizontal line test. The function f(a) = a² is used to indicate the parabola.

When we draw the horizontal line for this function, we will see that there are two points where it will intersect the parabola. Because of these two points, we have two outputs for one input. Hence, we can say that the parabola is not an injective function.

Injective function Inverse

If there is a function f, then the inverse of f will be denoted by f^-1. If we define a function as y = f(x), then its inverse will be defined as x = f^-1(y). In this case, f^-1 is defined from y to x. In the case of an inverse function, the codomain of f will become the domain of f-1, and the domain of f will become the codomain of f^-1.

The inverse is only contained by the injective function because these functions contain the one-to-one correspondences. It means that only one element of the domain will correspond with each element of the range.

Suppose we have a function f, which is defined as f: X → Y. Here, f will be invertible if there is a function g, which is defined as g: Y → X, in a way that we will get the starting value when we operate f{g(x)} or g{f(x)}. Now we will learn this by some examples, which are described as follows:

Example: In this example, we have f: X → Y, where f(x) = 5x + 7. For all x, y ∈ N is invertible.

Solution: HFor this, we will assume that y ∈ N. Where y = f(x) = 5x + 7 for x ∈ N.

Now we will solve the above equation like this:

y = 5x + 7

x = (y - 7) / 5

Suppose we specify h: Y → X with the help of h(y) = (y - 7) / 5

Again we specify h ∘ f(x) = h[f(x)] = h{5x + 7} = 5(y - 7) / 5 + 7 = x

And then we specify f ∘ h(y) = f[h(y)] = f((y - 7) / 5) = 5(y - 7) / 5 + 7 = y

Hence, we can say that f is an invertible function and h is the inverse of f.

Properties of Injective function

There are a lot of properties of the injective function. Some of them are described as follows:

• In the injective function, the range and domain contain the equivalent sets.
• There is equal amount of cardinal numbers in the domain and range sets of one-to-one functions.
• The one-to-one function is used to follow some properties, i.e., symmetric, reflexive, and transitive.
• When we draw a graph for an injective function, then that graph will always be a straight line.

Some more Examples of Injective function:

As we have learned examples of injective function, and now we will learn some more examples to understand this topic more.

Example 1: Suppose there are two sets X and Y. Here Set X = {1, 2, 3} and Y = {u, x, y, z}. Now we have to determine which one from the set is one to one function.

1. {(1, z), (2, z), (2, z)}
2. {(1, x), (2, y), (3, z)}
3. {(1, y), (1, z)}

Solution:

Here the correct answer is shown by option no 2 because, in set B (range), all the elements are uniquely mapped with all the elements of set A (domain).

Example 2: In this example, we have f: R→ R. Here f(x) = 3x³ - 4. Now we have to show that this function is one to one.

Solution:

For this example, we will assume that f(x₁) = f(x₂) for all x₁, x₂ ∈ R.

From this assumption we can say

3x₁³ - 4 = 3x₂³ - 4

x₁³ = x₂³

x₁³ - x₂³ = 0

(x₁ - x₂) (x₁ + x₁x₂ + x₂²) = 0

x₁ = x₂ and (x₁2 + x₁x₂2 + x₂²) = 0

As x₁ and x₁ does not contain any real values. That's why we cannot consider (x₁² + x₁x₂² + x₂²) = 0.

Hence, the given function f(x) = 3x³ - 4 is one to one.

Example 3: In this example, we have two functions f(x) and g(x). Where f(x) = x + 1 and g(x) = 2x + 3. Now we have to determine gof(x) and also have to determine whether this function is injective function.

Solution: As we know we have f(x) = x + 1 and g(x) = 2x + 3. To determine the gof(x) we have to combine both the functions.

g(f(x)) = g(x + 1) = 2(x + 1) + 3 = 2x + 2 + 3 = 2x + 5

gof(x) = 2x + 5

In the domain of this composite function, we will consider the first 5 natural numbers like this:

When x = 1, 2, 3, 4, and 5, we will get the following:

gof(1) = 2(1) + 5 = 2 + 5 = 7

gof(2) = 2(2) + 5 = 4 + 5 = 9

gof(3) = 2(3) + 5 = 6 + 5 = 11

gof(4) = 2(4) + 5 = 8 + 5 = 13

gof(5) = 2(5) + 5 = 10 + 5 = 15

Thus, gof(x) = {(1, 7), (2, 9), (3, 11), (4, 13), (5, 15)}.

With the help of value of gof(x) we can say that a distinct element in the domain is mapped with the distinct image in the range.

Therefore, the above function is a one-to-one or injective function.