Integer DefinitionThe word "integer" comes from the Latin, and it is used for expressing "whole" or "intact". Because of this, fractions and decimals are not considered integers. In math, Integers play a crucial role in various ways. Let us read this article to learn more about integers, their definitions, and their characteristics. What is an Integer?A numerical value or a number is said to be an integer if it is a whole number, be it positive or negative. Therefore, the three types of integers are positive, negative, and zero. Accordingly, a set of integers is formed if we combine multiple positive whole numbers and/ or negative numbers without fractions and decimals. The group of counting numbers that can be expressed without the need for a fractional component also includes a zero. So, as was already established, an integer can be either positive, negative, or zero. Integers with a base of 1 and an infinite range make up all natural numbers. Beginning at 0 and going all the way to infinity on both sides (positive and negative), all whole numbers are integers. Integer can be represented as below: …… -3, -2, -1, 0, 1, 2, 3…… Integers, which can comprise positive and negative numbers, including zero, represent the numbers without a decimal or fractional component. The following are a few random examples of integers: -4, 0, 1, 3, 7, 99, and 4960. Classification of IntegersIntegers are mainly categorized into the following three categories: 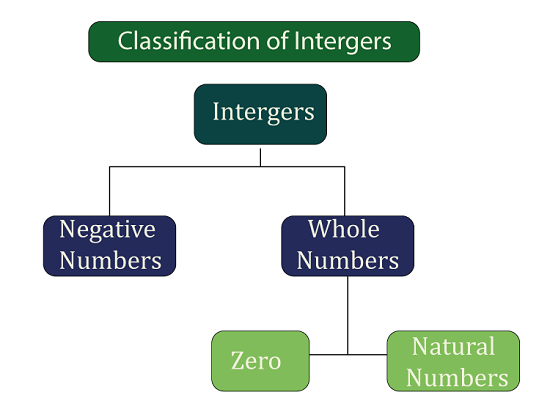
Example: Z = (1, 2, 3), etc.
Example: Z = (-1, -2, -3), etc.
Example: Z = (0) In all the above examples, Z is an integer set that consists of the respective integers. Integers on Number LinesA straight line of numbers is shown visually as a number line. This line is used to compare integers spaced equally apart on an infinite line extending horizontally on both sides. The collection of integers can be shown on a number line, much like other numbers. 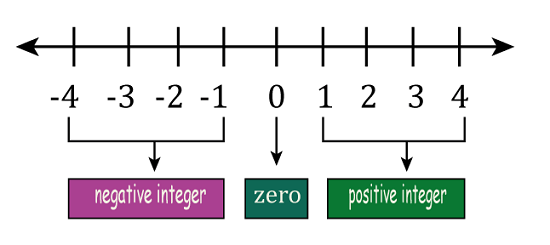
Graphing Integers on a Number LineNumber lines can be used to depict both positive and negative numbers visually. A number line's integers assist in carrying out mathematical operations. While arranging numbers on a number line, it is important to keep the following in mind:
In the following image, the integers -6, -2, and 3 are graphed on a number line with a pink colored circle (dot): 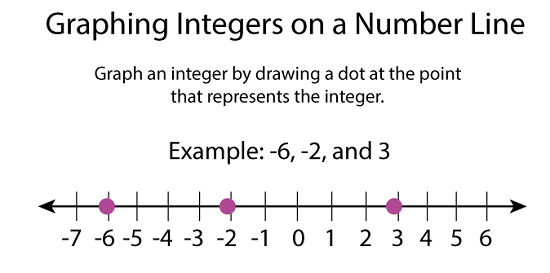
Integer OperationsIntegers can be used in the following four fundamental arithmetic operations:
Let us understand each in detail: Addition of IntegersCalculating the sum between two or more integers is the process of adding them, and depending on whether they are positive or negative, the value may increase or decrease. The following section lists the many guidelines and potential scenarios for adding integers. Guidelines for Adding Integers We employ the following principles when adding two integers:
Example 5 + 8 = 13 -5 + (-8) = -13 The output will contain the signature of the greater integer if any of the integers has a different orientation, resulting in subtraction. Let us clarify with the use of examples: (-10) + (2) = -10 + 2 = -8 (-2) + (10) = -2 + 10 = 8 That is how the addition of integers works. Subtraction of IntegersDetermining the differences between two or more integers and allowing for the possibility that the result may be positive or negative, subtracting integers involves finding the differential value between the integers. The next section will review the various guidelines and potential scenarios for subtracting integers. Rules of Integer in Subtraction The following guidelines are used when subtracting two integers:
Example 7 - 10 = -3 Now, let us discuss the operation process for this calculation. First, change the sign of the subtractor to produce the following result (by converting the provided statement to look like an addition problem): 7 + (-10) The guidelines for this operation will now be the same as those for adding two numbers. In this instance, the absolute values of 7 and (-10) are 7 and 10, respectively. They differ by 10 - 7 (bigger number - smaller number), which equals 3. Since 'ten' is the greater number in this instance, and so the output (result) bears its original sign, i.e., "-", instead of the sign of the seven. As a result, the outcome is denoted by the "-". As a result, 7 - 10 = -3 Multiplication of IntegerThe rules listed in the following table are used for multiplying whole numbers (or integers). The following section lists the many methods for multiplying integers and the scenarios in which they might be used. Here, we can determine which sign we should use with the output value when multiplying two integers of the same or different signs:
Example Now, observe the following multiplication where we have integers 4 and 2. Although results seem the same in numbers, they differ because of their resultant sign, plus or minus: 4 x 2 = 8 4 x (-2) = -8 (-4) x 2 = -8 (-4) x 2 = 8 Division of IntegerWhen an integer is divided, it is either evenly divided into groups or a predetermined number of groups. We follow the guidelines listed in the following table when dividing integers. The following section determines which sign we should use with the output value when dividing two integers of the same or different signs:
Example Now, observe the following division where we have integers 10 and 2. Like the multiplication of integers, the results in integers division also seem the same in numbers, but they differ because of their resultant sign, plus or minus: 10 ÷ 2 = 5 10 ÷ 2 = -5 (10) ÷ 2 = -5 (-10) ÷ (-2) = 5 Properties of IntegersListed below are the integers' primary characteristics: Closure PropertyAccording to the set's closure property, it can be mathematically closed for every given operation. Under integer addition, subtraction, multiplication, & division, Z is closed, meaning that the output (result) will also be an integer. When given any two integers a and b, the closure property states:
Where Z depicts a set of integers. For instance, 2 + 8 = 10 (which is an integer) 2 x 8 = 16 (which is an integer) Associative PropertyThe associative property states that altering how two integers are grouped will not change the operation's outcome. Two integers can be added together and multiplied using the associative property. Suppose a and b are any two integers, so the associative property states:
For instance, 2 + (4 + 4) = (2 + 4) + 4 = 10 2 x (3 × 4) = (2 × 3) x 4 = 24 It is essential to note that the associative property is not applicable to the subtraction and division of integers. Commutative PropertyThe commutative property states that an operation's outcome is unaffected by the order in which its operands are used. Integers are added and multiplied following the commutative property. Suppose a and b are any two integers, so the commutative property states:
Similar to the associative property, the commutative property is also not applicable to the subtraction and division of integers. For instance, 2 + 8 = 8 + 2 = 10 2 x 8 = 8 x 2 = 16 Distributive PropertyAccording to the distributive property, any phrase of form a (b + c), which denotes the form "x (b + c)", allows the operand a to be divided among operands b and c as follows: (a × b) + (a × c), As a result,
For instance, Let us prove that: 4 x (4 + 1) = 4 x 4 + 4 x 1 LHS = 4 x (4 + 1) = 4 x 5 = 20 RHS = 4 x 4 + 4 x 1 = 16 + 4 = 20 Since LHS (which is 20) = RHS (which is also 20). Hence, the distributive property is proven to be true. Additive Inverse PropertyAccording to the additive inverse property, when adding a specific integer to its positive and negative values, zero (0) is the only result. Whatever the integer a is, the additive inverse property states:
In this way, -a is called the additive inverse of integer a. Multiplicative Inverse PropertyAccording to the multiplicative inverse property, the outcome is always one (1) when an integer is multiplied by its reciprocal. Whatever the integer a is, the multiplicative inverse property states:
In this way, 1/a is the multiplicative inverse of integer a. Identity PropertyWhen performing addition and multiplication operations, integers adhere to the identity property. According to the additive identity property, an integer becomes the integer itself when a zero is added to it. As a result, this illustrates:
Similarly, according to the multiplicative identity property, multiplying one by any integer yields the integer. As a result, this illustrates:
Comparing the IntegersIntegers can be compared in the same way as positive whole numbers. We can quickly compare the integers by utilizing a number line. The value of a number increases as it moves further to the right. A number line is expressed like this: ……-8,-7,-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8,…… For instance, let us now compare integers -8 and -2. People will argue that the integer -8 is bigger than -2, but this is not true. As already said, the value rises as you turn to the right. So, the value does not decrease with the smaller negative numbers but increases. If we check the integers on a number line, we can easily notice the integer -2 on the right side of -8. Because of this, -2 is more than -8, or -2 > -8. Likewise, in another instance, let us consider integers -8 and 3. Although it may appear at first glance that integer -8 is greater than 3, it is not the case again. One universal rule is that negative values are never greater than positive ones. Also, one can see that the integer 3 stands at the right of the integer -8. This demonstrates that 3 is more than -8, or 3 > -8.
Next TopicLeadership Definition
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










