Inverse of a Matrix in Discrete mathematicsIf we want to determine the inverse of a matrix, then we have to first learn about the matrix. A matrix can be described as a collection of objects which are arranged in rows and columns. We can call these types of objects as elements of a matrix. In the form of a number of rows by a number of columns, we can write the order of any matrix. For example: 2*2, 3*3, 2*3, and many more. If the given matrix is a square matrix, only then we can determine the inverse of that matrix. A matrix will be known as the square matrix if it has the same number of rows and columns, i.e., 2*2, 3*3, 4*4, etc. In other words, the inverse matrix can be described as a matrix which will be obtained by dividing the adjugate of matrix by the determinant of that matrix. In this section, we will learn the inverse of a matrix, the use of different methods to find the inverse matrix, its properties and examples. Inverse of a MatrixSuppose there is a non-singular square matrix A. The inverse of matrix A will be represented by A-1. There are some properties which must be satisfied by the inverse matrix, which is described as follows: 1. If we multiply a matrix A and its inverse matrix A-1, then the result of multiplication will be an identity matrix. AA-1 = A-1A = I, 'I' is used to indicate the identity matrix. For example: Suppose there is a 2*2 matrix. The identity matrix of this matrix is described as follows: 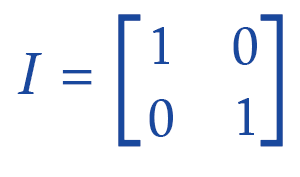
While doing this, we usually get some number like 4 or -7. When we try to inverse these types of numbers, then its inverse will be 1/4 or -1/7, and when we multiply these numbers with the number 4 or -7, then we will get the identity number as a result. 2. If there is a square matrix and we want to calculate the inverse matrix, then the matrix must be non-singular, and the determinant value of this matrix must be 0. For example: Suppose there is a square matrix A, which is described as follows: 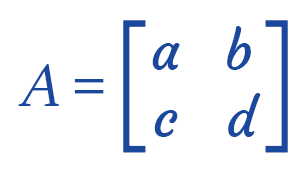
Here, a, b, c and D are used to indicate the numbers. In the above matrix, the determinant can be written as ad-bc. For the existence of the inverse, the value of the determinant must not be 0. For the matrices 2*2, 3*3, 4*4, ... n*n, we can find the inverse of a matrix. If we try to find the inverse of matrix 2*2, then it will be simple as compared to finding the inverse of matrix 3*3. Method of Inverse matrixWe have three different methods through which we can find the inverse of a matrix. The same output will be generated by all of these three methods. Method 1: 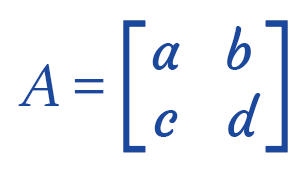
With the help of following formula, we can find the inverse of a matrix: 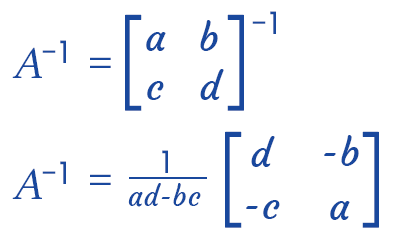
Similarly, if we determine the determinant value of a given matrix 3*3, then we will be able to determine the inverse of matrix 3*3. Method 2: This method is the most important and useful method to determine the inverse matrix. With the help of determining the minors and cofactor of elements of the given matrix, we can determine the inverse of a matrix. Now we will understand this method with the help of following steps:
Where det(A) is used to indicate the determinant of a matrix A and adj(A) is used to indicate the adjoint of a matrix A
We can determine the adjoint of a matrix A with the help of first determining the cofactor matrix of a given matrix, and after that, we will take the transpose of a cofactor matrix.
Cij = (-1)i+j det(Mij) Here Mij is used to indicate the (i, j)th minor matrix when we remove the ith row and jth column. The adjoint of a matrix A can also be known as the transpose of a cofactor matrix. Similarly, if we want to determine the 3*3 matrix, then we can also do this. In the 3*3 matrix, our first step will also be to determine the determinant, and the second step will also be the transpose. Method 3: In this method, we will assume three matrices, X, A and B, in such a way that X = AB. With the help of an elementary matrix, we can find the inverse of a matrix. In this process, we have to convert the given matrix into the identity matrix. If there is an inverse matrix A-1 of the matrix A, then we can find A-1 with the help of an elementary row operation like this:
Formula of Inverse matrixSuppose there is a 2*2 matrix, which is described as follows: 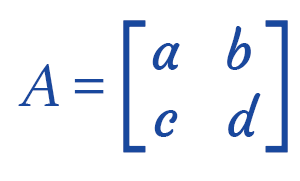
With the help of following formula, we can find the inverse of 2*2 matrices: 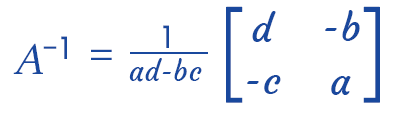
Now we will assume a 3*3 matrix, which is described as follows: 
With the help of following formula, we can find the inverse of 3*3 matrices like this: 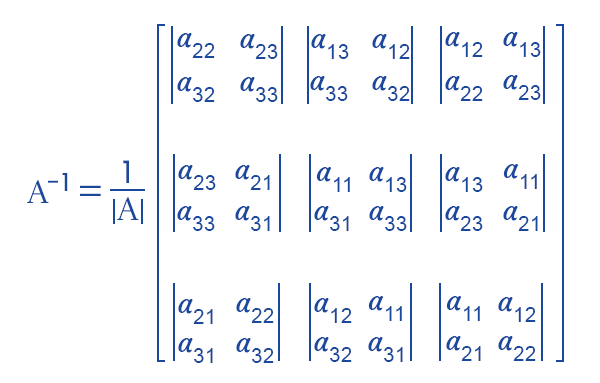
Example of Inverse matrixNow we will use the following example to understand the inverse of a matrix. Example 1: In this example, we will find the inverse of 2*2 matrix, which is described as follows: 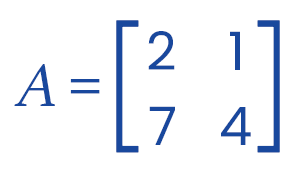
Solution: Suppose A = IA 
Now we will apply R1 → (1/2)R1 in the above matrix and get the following: 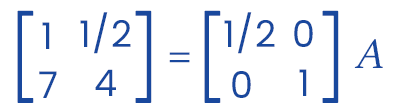
We will apply R2 → R2 - 7R1 in the above matrix and get the following: 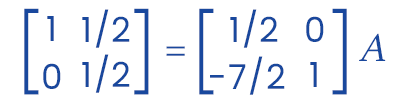
Now we will apply the R2 → 2R2 in the above matrix and get the following: 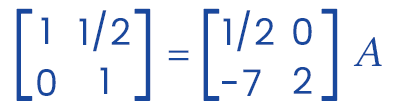
We will apply R1 → R1 - (1/2)R2 and get the following: 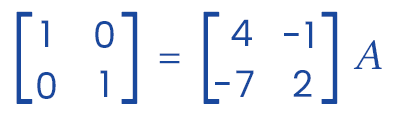
Thus, we will get the inverse of matrix A like this: I = A-1A. Therefore, 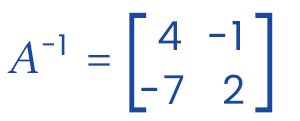
Example 2: In this example, we will find the inverse of 3*3 matrix, which is described as follows: 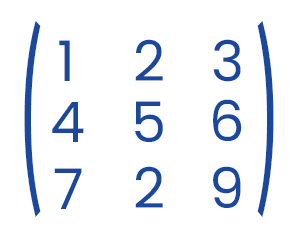
Solution: First, we will show the determinant of the above matrix like this: 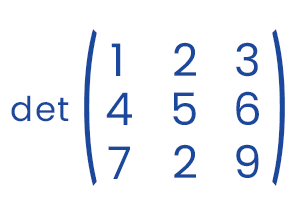
= 1.33 - 2(-6) +3(-27) = -36 Now we will determine the minors of the given matrix like this: 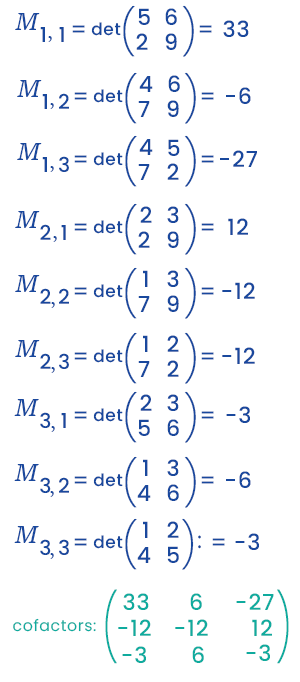
Now we will use the transpose of cofactor of a given matrix and try to determine the adjoint of a matrix like this: 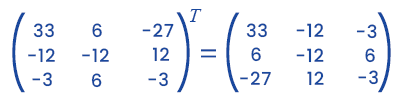
Now, A-1 = (1 / |A|) Adj A Hence, we will get the inverse of given matrix A like this: 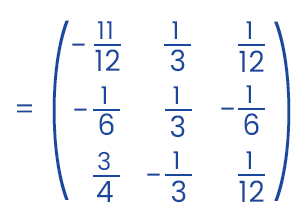
Properties of Inverse of a matrixThere are some important properties of the inverse matrix, which are described as follows:
Question related to Inverse matrixWhen we learn about the inverse of a matrix, a question occurred in our mind: "is it possible to do the inverse of every matrix?" Solution: To understand this concept, we will take the number 0. So if we multiply 0 by any number, then there is no chance that we will get 1. That means there is no multiplicative inverse of the number 0. Similarly, every matrix does not have its inverse. The inverse matrix can only be possible if the given matrix is the square matrix, and even after that, it is not compulsory that the given matrix is invertible. The matrix can be known as the square matrix if it contains the same number of rows and columns. We can use the following terminology if we are talking about a matrix, whether it has an inverse or not.
Often, it is not possible for us to look at the matrix and decide whether it is invertible or not. We can understand this with the help of following example: 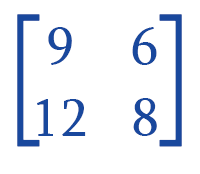
The above matrix is not invertible. This is because it does not have any matrix that we can multiply to this matrix and get the identity matrix.
Next TopicInverse property in Discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










