Java program to construct a Binary Search Tree and perform deletion and In-order traversal

In this program, we need to create a binary search tree, delete a node from the tree, and display the nodes of the tree by traversing the tree using in-order traversal. In in-order traversal, for a given node, first, we traverse the left child then root then right child (Left -> Root -> Right).

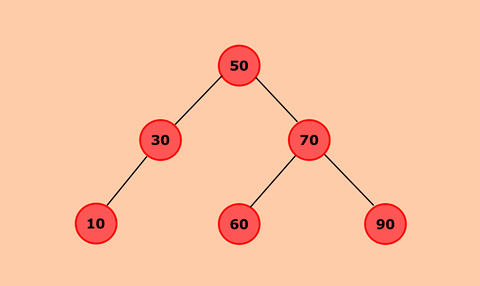
In Binary Search Tree, all nodes which are present to the left of root will be less than root node and nodes which are present to the right will be greater than the root node.

Insertion:

If the value of the new node is less than the root node then, it will be inserted to the left subtree.
If the value of the new node is greater than root node then, it will be inserted to the right subtree.

Deletion:

If the node to be deleted is a leaf node then, parent of that node will point to null. For eg. If we delete 90, then parent node 70 will point to null.
If the node to be deleted has one child node, then child node will become a child node of the parent node. For eg. If we delete 30, then node 10 which was left child of 30 will become left child of 50.
If the node to be deleted has two children then, we find the node(minNode) with minimum value from the right subtree of that current node. The current node will be replaced by its successor(minNode).

Algorithm

Define Node class which has three attributes namely: data, left and right. Here, left represents the left child of the node and right represents the right child of the node.
When a node is created, data will pass to the data attribute of the node and both left and right will be set to null.
Define another class which has an attribute root.
- Root represents the root node of the tree and initializes it to null.

a. insert() will insert the new value into a binary search tree:

It checks whether root is null, which means tree is empty. New node will become root node of tree.
If tree is not empty, it will compare value of new node with root node. If value of new node is greater than root, new node will be inserted to right subtree. Else, it will be inserted in left subtree.

a. deleteNode() will delete a particular node from the tree:

If value of node to be deleted is less than root node, search node in left subtree. Else, search in right subtree.
If node is found and it has no children, then set the node to null.
If node has one child then, child node will take position of node.
If node has two children then, find a minimum value node from its right subtree. This minimum value node will replace the current node.

Program:

public class BinarySearchTree {

    //Represent a node of binary tree
    public static class Node{
        int data;
        Node left;
        Node right;

        public Node(int data){
            //Assign data to the new node, set left and right children to null
            this.data = data;
            this.left = null;
            this.right = null;
        }
      }

      //Represent the root of binary tree
      public Node root;

      public BinarySearchTree(){
          root = null;
      }

      //insert() will add new node to the binary search tree
      public void insert(int data) {
          //Create a new node
          Node newNode = new Node(data);

          //Check whether tree is empty
          if(root == null){
              root = newNode;
              return;
            }
          else {
              //current node point to root of the tree
              Node current = root, parent = null;

              while(true) {
                  //parent keep track of the parent node of current node.
                  parent = current;

                  //If data is less than current's data, node will be inserted to the left of tree
                  if(data < current.data) {
                      current = current.left;
                      if(current == null) {
                          parent.left = newNode;
                          return;
                      }
                  }
                  //If data is greater than current's data, node will be inserted to the right of tree
                  else {
                      current = current.right;
                      if(current == null) {
                          parent.right = newNode;
                          return;
                      }
                  }
              }
          }
      }

      //minNode() will find out the minimum node
      public Node minNode(Node root) {
          if (root.left != null)
              return minNode(root.left);
          else
              return root;
      }

      //deleteNode() will delete the given node from the binary search tree
      public Node deleteNode(Node node, int value) {
          if(node == null){
              return null;
           }
          else {
              //value is less than node's data then, search the value in left subtree
              if(value < node.data)
                  node.left = deleteNode(node.left, value);

              //value is greater than node's data then, search the value in right subtree
              else if(value > node.data)
                  node.right = deleteNode(node.right, value);

              //If value is equal to node's data that is, we have found the node to be deleted
              else {
                  //If node to be deleted has no child then, set the node to null
                  if(node.left == null && node.right == null)
                      node = null;

                  //If node to be deleted has only one right child
                  else if(node.left == null) {
                      node = node.right;
                  }

                  //If node to be deleted has only one left child
                  else if(node.right == null) {
                      node = node.left;
                  }

                  //If node to be deleted has two children node
                  else {
                      //then find the minimum node from right subtree
                      Node temp = minNode(node.right);
                      //Exchange the data between node and temp
                      node.data = temp.data;
                      //Delete the node duplicate node from right subtree
                      node.right = deleteNode(node.right, temp.data);
                  }
              }
              return node;
          }
      }

      //inorder() will perform inorder traversal on binary search tree
      public void inorderTraversal(Node node) {

          //Check whether tree is empty
          if(root == null){
              System.out.println("Tree is empty");
              return;
           }
          else {

              if(node.left!= null)
                  inorderTraversal(node.left);
              System.out.print(node.data + " ");
              if(node.right!= null)
                  inorderTraversal(node.right);

          }
      }

      public static void main(String[] args) {

          BinarySearchTree bt = new BinarySearchTree();
          //Add nodes to the binary tree
          bt.insert(50);
          bt.insert(30);
          bt.insert(70);
          bt.insert(60);
          bt.insert(10);
          bt.insert(90);

          System.out.println("Binary search tree after insertion:");
          //Displays the binary tree
          bt.inorderTraversal(bt.root);

          Node deletedNode = null;
          //Deletes node 90 which has no child
          deletedNode = bt.deleteNode(bt.root, 90);
          System.out.println("\nBinary search tree after deleting node 90:");
          bt.inorderTraversal(bt.root);

          //Deletes node 30 which has one child
          deletedNode = bt.deleteNode(bt.root, 30);
          System.out.println("\nBinary search tree after deleting node 30:");
          bt.inorderTraversal(bt.root);

          //Deletes node 50 which has two children
          deletedNode = bt.deleteNode(bt.root, 50);
          System.out.println("\nBinary search tree after deleting node 50:");
          bt.inorderTraversal(bt.root);
      }
}

Output:

Binary search tree after insertion:
10 30 50 60 70 90 
Binary search tree after deleting node 90:
10 30 50 60 70 
Binary search tree after deleting node 30:
10 50 60 70 
Binary search tree after deleting node 50:
10 60 70

Next TopicJava Programs

← prev next →