Java program to find the total number of possible Binary Search Trees with N keys

In this program, we need to find out the total number of binary search trees can be constructed with n values. Below diagram shows a possible binary search tree with the key value as 3. So, we can construct a total of five binary search trees. When we choose node 1 as the root node, we get two trees. Similarly, one tree with 2 as root nodes and two trees when we select 3 as the root node.

This approach involves selecting a node recursively as the root node and create possible binary search tree.

An easy way to calculate the total number of possible binary search trees are through Catalan number: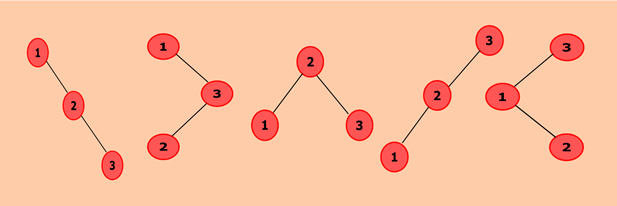

Algorithm

• Define Node class which has three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.
• When a node is created, data will be passed to the data attribute of the node and both left and right will be set to null.
• Define another class which has an attribute root.
  • Root represents the root node of the tree and initializes it to null.

a. numOfBST() will find out total possible binary search tree for given key:

• It will calculate the Catalan number for given key by making a call to factorial().
• Catalan number can be calculated using the formula:
  Cn = (2n)! / n! *(n+1)!
• Factorial() will calculate factorial of a given number.

Program:

Output:

Total number of possible Binary Search Trees with given key: 42