K-Medoids clustering-Theoretical Explanation

K-Medoids and K-Means are two types of clustering mechanisms in Partition Clustering. First, Clustering is the process of breaking down an abstract group of data points/ objects into classes of similar objects such that all the objects in one cluster have similar traits. , a group of n objects is broken down into k number of clusters based on their similarities.

Two statisticians, Leonard Kaufman, and Peter J. Rousseeuw came up with this method. This tutorial explains what K-Medoids do, their applications, and the difference between K-Means and K-Medoids.

K-medoids is an unsupervised method with unlabelled data to be clustered. It is an improvised version of the K-Means algorithm mainly designed to deal with outlier data sensitivity. Compared to other partitioning algorithms, the algorithm is simple, fast, and easy to implement.

The partitioning will be carried on such that:

1. Each cluster must have at least one object
2. An object must belong to only one cluster

Here is a small recap on K-Means clustering:

In the K-Means algorithm, given the value of k and unlabelled data:

1. Choose k number of random points (Data point from the data set or some other points). These points are also called "Centroids" or "Means".
2. Assign all the data points in the data set to the closest centroid by applying any distance formula like Euclidian distance, Manhattan distance, etc.
3. Now, choose new centroids by calculating the mean of all the data points in the clusters and goto step 2
4. Continue step 3 until no data point changes classification between two iterations.

The problem with the K-Means algorithm is that the algorithm needs to handle outlier data. An outlier is a point different from the rest of the points. All the outlier data points show up in a different cluster and will attract other clusters to merge with it. Outlier data increases the mean of a cluster by up to 10 units. Hence, K-Means clustering is highly affected by outlier data.

K-Medoids:

Medoid: A Medoid is a point in the cluster from which the sum of distances to other data points is minimal.

(or)

A Medoid is a point in the cluster from which dissimilarities with all the other points in the clusters are minimal.

Instead of centroids as reference points in K-Means algorithms, the K-Medoids algorithm takes a Medoid as a reference point.

There are three types of algorithms for K-Medoids Clustering:

1. PAM (Partitioning Around Clustering)
2. CLARA (Clustering Large Applications)
3. CLARANS (Randomized Clustering Large Applications)

PAM is the most powerful algorithm of the three algorithms but has the disadvantage of time complexity. The following K-Medoids are performed using PAM. In the further parts, we'll see what CLARA and CLARANS are.

Algorithm:

Given the value of k and unlabelled data:

1. Choose k number of random points from the data and assign these k points to k number of clusters. These are the initial medoids.
2. For all the remaining data points, calculate the distance from each medoid and assign it to the cluster with the nearest medoid.
3. Calculate the total cost (Sum of all the distances from all the data points to the medoids)
4. Select a random point as the new medoid and swap it with the previous medoid. Repeat 2 and 3 steps.
5. If the total cost of the new medoid is less than that of the previous medoid, make the new medoid permanent and repeat step 4.
6. If the total cost of the new medoid is greater than the cost of the previous medoid, undo the swap and repeat step 4.
7. The Repetitions have to continue until no change is encountered with new medoids to classify data points.

Here is an example to make the theory clear:

Data set:

Scatter plot: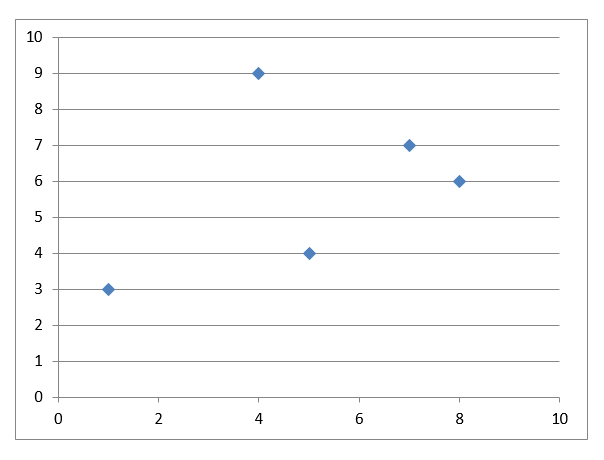

If k is given as 2, we need to break down the data points into 2 clusters.

1. Initial medoids: M1(1, 3) and M2(4, 9)
2. Calculation of distances

Manhattan Distance: |x1 - x2| + |y1 - y2|

Cluster 1: 0

Cluster 2: 1, 3

1. Calculation of total cost:
   (5) + (5 + 7) = 17
2. Random medoid: (5, 4)

M1(5, 4) and M2(4, 9):

Cluster 1: 2, 3

Cluster 2: 1

1. Calculation of total cost:
   (5 + 5) + 5 = 15
   Less than the previous cost
   New medoid: (5, 4).
2. Random medoid: (7, 7)

M1(5, 4) and M2(7, 7)

Cluster 1: 2

Cluster 2: 3, 4

1. Calculation of total cost:
   (5) + (2 + 5) = 12
   Less than the previous cost
   New medoid: (7, 7).
2. Random medoid: (8, 6)

M1(7, 7) and M2(8, 6)

Cluster 1: 4

Cluster 2: 0, 2

1. Calculation of total cost:
   (5) + (5 + 10) = 20
   Greater than the previous cost
   UNDO
   Hence, the final medoids: M1(5, 4) and M2(7, 7)
   Cluster 1: 2
   Cluster 2: 3, 4
   Total cost: 12
   Clusters:

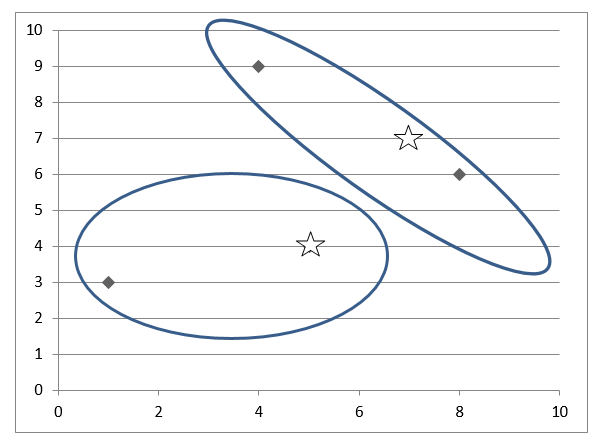
Limitation of PAM:

Time complexity: O(k * (n - k)²)

Possible combinations for every node: k*(n - k)

Cost for each computation: (n - k)

Total cost: k*(n - k)²

Hence, PAM is suitable and recommended to be used for small data sets.

CLARA:

It is an extension to PAM to support Medoid clustering for large data sets. This algorithm selects data samples from the data set, applies Pam on each sample, and outputs the best Clustering out of these samples. This is more effective than PAM. We should ensure that the selected samples aren't biased as they affect the Clustering of the whole data.

CLARANS:

This algorithm selects a sample of neighbors to examine instead of selecting samples from the data set. In every step, it examines the neighbors of every node. The time complexity of this algorithm is O(n²), and this is the best and most efficient Medoids algorithm of all.

Advantages of using K-Medoids:

1. Deals with noise and outlier data effectively
2. Easily implementable and simple to understand
3. Faster compared to other partitioning algorithms

Disadvantages:

1. Not suitable for Clustering arbitrarily shaped groups of data points.
2. As the initial medoids are chosen randomly, the results might vary based on the choice in different runs.

K-Means and K-Medoids:

Useful Outlier Clusters:

For suppose, A data set with data on people's income is being clustered to analyze and understand individuals' purchasing and investing behavior within each cluster.

Here outlier data will be people with high incomes-billionaires. All such people tend to purchase and invest more. Hence, a separate cluster for billionaires would be useful in this scenario.

In K-Medoids, It merges this data into the upper-class cluster, which loses the meaningful outlier data in Clustering and is one of the disadvantages of K-Medoids in special situations.