Karnaugh Map(K-Map) methodThe K-map is a systematic way of simplifying Boolean expressions. With the help of the K-map method, we can find the simplest POS and SOP expression, which is known as the minimum expression. The K-map provides a cookbook for simplification. Just like the truth table, a K-map contains all the possible values of input variables and their corresponding output values. However, in K-map, the values are stored in cells of the array. In each cell, a binary value of each input variable is stored. The K-map method is used for expressions containing 2, 3, 4, and 5 variables. For a higher number of variables, there is another method used for simplification called the Quine-McClusky method. In K-map, the number of cells is similar to the total number of variable input combinations. For example, if the number of variables is three, the number of cells is 23=8, and if the number of variables is four, the number of cells is 24. The K-map takes the SOP and POS forms. The K-map grid is filled using 0's and 1's. The K-map is solved by making groups. There are the following steps used to solve the expressions using K-map:
2 Variable K-mapThere is a total of 4 variables in a 2-variable K-map. There are two variables in the 2-variable K-map. The following figure shows the structure of the 2-variable K-map: 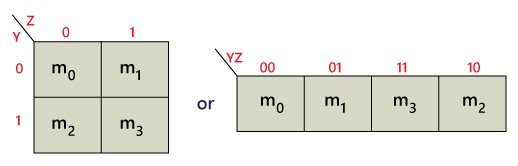
3-variable K-mapThe 3-variable K-map is represented as an array of eight cells. In this case, we used A, B, and C for the variable. We can use any letter for the names of the variables. The binary values of variables A and B are along the left side, and the values of C are across the top. The value of the given cell is the binary values of A and B at left side in the same row combined with the value of C at the top in the same column. For example, the cell in the upper left corner has a binary value of 000, and the cell in the lower right corner has a binary value of 101. 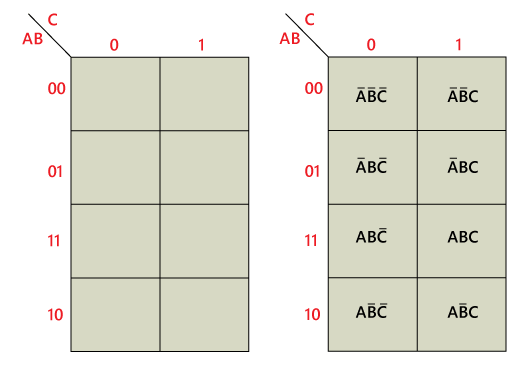
The 4-Variable Karnaugh MapThe 4-variable K-map is represented as an array of 16 cells. Binary values of A and B are along the left side, and the values of C and D are across the top. The value of the given cell is the binary values of A and B at left side in the same row combined with the binary values of C and D at the top in the same column. For example, the cell in the upper right corner has a binary value of 0010, and the cell in the lower right corner has a binary value of 1010 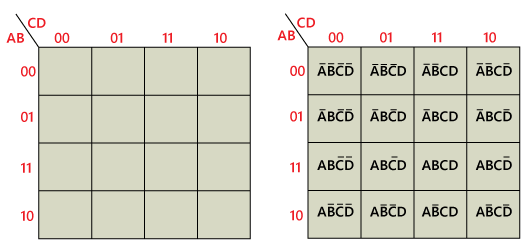
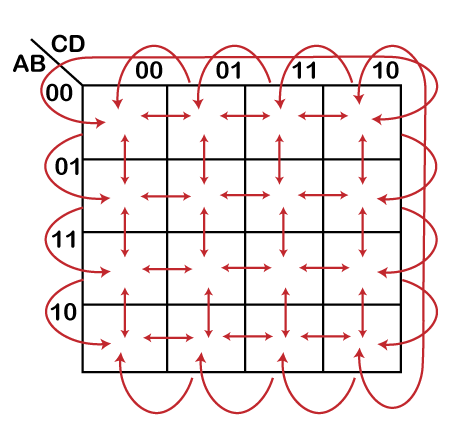
5-variable K-mapWith the help of the 32- cell K-map, the boolean expression with 5 variables can be simplified. For constructing a 5-variable K-map, we use two 4-variable K-maps. The cell adjacencies within each of the 4- variable maps for the 5-variable map are similar to the 4- variable map. A K-map for five variables (PQRST) can be constructed using two 4-variable maps. Each map contains 16 cells with all combinations of variables Q, R, S, and T. One map is for P = 0, and the other is for P = 1). 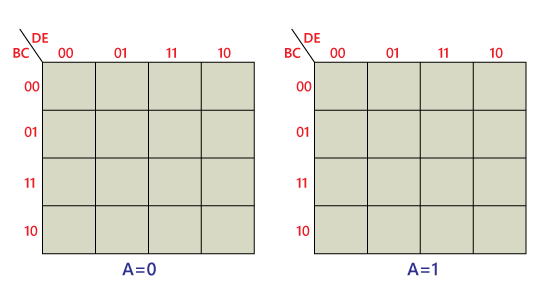
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










