Konigsberg Bridge Problem in Discrete mathematics

Konigsberg

• The Konigsberg is the name of the German city, but this city is now in Russia.
• In the below image, we can see the inner city of Konigsberg with the river Pregel.
• There are a total of four land areas in which this river Pregel is divided, i.e., A, B, C and D.
• There are total 7 bridges to travel from one part of the city to another part of the city.

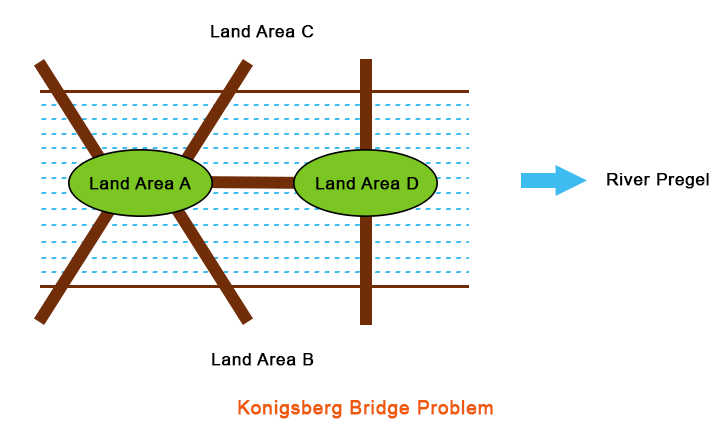
Konigsberg Bridge problem

The Konigsberg Bridge contains the following problem which says:

Is it possible for anyone to cross each of the seven bridges only a single time and come back to the beginning point without swimming across the river if we begin this process from any of the four land areas that are A, B, C, and D?.

Solution of Konigsberg Bridge problem

• In 1735, this problem was solved by Swiss mathematician Leon hard Euler.
• According to the solution to this problem, these types of walks are not possible.

With the help of following graph, Euler shows the given solution.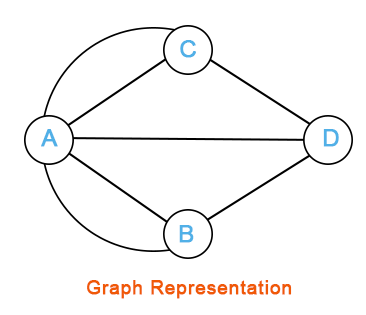

In the above graph, the following things have:

• The vertices of this graph are used to show the landmasses.
• The edges are used to show the bridges.

Now we will consider an image and try to understand the concept of Konigsberg Bridge: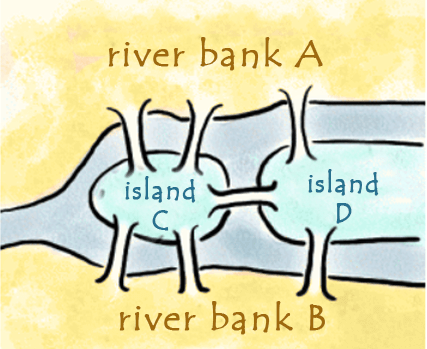

For the citizens of Konigsberg, it became a tradition in which they tried to walk around the town in such a way that they crossed each bridge only a single time, but it proved to be a difficult problem. So, in the end, Euler proved that this type of walk is not possible. Euler proved it with the help of inventing a kind of diagram, which is known as the network. This network is made up of arcs and vertices. The arcs are also known as lines, and vertices are also known as dots where lines meet.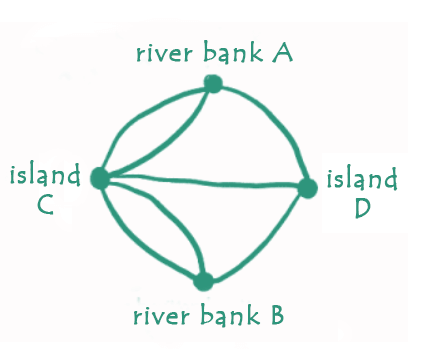

In this diagram, he used two islands and 4 dots (vertices) for two riverbanks. With the help of A, B, C, and D, these dots have been marked. The 7 lines (arcs) are used to show the seven bridges. In the above diagram, 3 bridges (arcs) were used to join riverbank A, and 3 arcs were used to join riverbank B. As same, 5 bridges (arcs) were used to join island C, and 3 arcs were used to join island D. This shows that all the vertices of this network contain an odd number of arcs, so these types of vertices are called odd vertices. (For an even vertex, there must be an even number of bridges joining to it).

We have to keep in mind that the problem of Konigsberg was to travel around the town by crossing each bridge only a single time. On Euler's network, it meant that all the vertices had to be visited and traced over each arc only a single time. He worked on it and said that it would not be done, because to do this, we want the odd vertex, and for odd vertex, the trip must start and end at that vertex. So there can be only 2 odd vertices, and there can be only one starting and one end only if we can trace over each arc only once. Since there is a total of 4 odd vertices in the bridge, so it would not be possible to do.

So Euler observed that at the time of tracing the graph, if they try to visit a vertex, then the following things happen:

• The graph will contain an edge that enters into the vertex.
• It will contain one more edge that leaves the vertex.
• Therefore, there must be an even number in the order of vertex.

On the basis of the above observation, Euler also discovers one thing about a network, i.e., with the help of a number of odd vertices which exists in the network is used to determine whether any network is traversable or not.

About the network, Euler found that if a network contains the following things, only then that network will be traversable:

• The network does not contain any odd vertices. Here, the starting vertex and the end vertex must be the same. The starting vertex can be any vertex, but the ending point must be at the same starting vertex.
• Or the network contains two odd vertices. Here, the beginning point must be the one odd vertex, and the endpoint must be the other odd vertex.

Now,

• Since there are total 4 odd vertices in the Konigsberg network, therefore Euler concluded that the network is not traversable.
• Thus, Euler finally concluded that it is not possible to traverse the desired walking tour of Konigsberg.

Note:

If the Konigsberg citizens want to build eight bridges from one land to another land, i.e., from A to C, then it will contain the following property:

• It will be possible for them to do a walk without even traversing any bride twice.
• Because of this, it will contain exactly two odd vertices.
• However, if we try to add the ninth bridge, then because of this, the walking tour will once again become impossible.

Lastly, we have a question what happens if the network does not contain the odd vertices at all? Can the network be traced in this situation?

The diagram of even vertices is described as follows: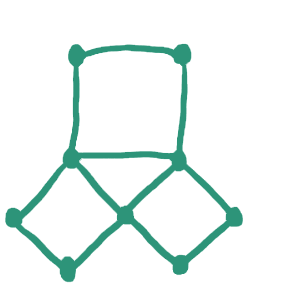

When the invention of a network was going on, a totally new type of geometry was found, which is known as the Topology. At this time, we are using topology in a lot of ways, like planning and mapping railway networks.