Kruskal's AlgorithmIn this article, we will discuss Kruskal's algorithm. Here, we will also see the complexity, working, example, and implementation of the Kruskal's algorithm. But before moving directly towards the algorithm, we should first understand the basic terms such as spanning tree and minimum spanning tree. Spanning tree - A spanning tree is the subgraph of an undirected connected graph. Minimum Spanning tree - Minimum spanning tree can be defined as the spanning tree in which the sum of the weights of the edge is minimum. The weight of the spanning tree is the sum of the weights given to the edges of the spanning tree. Now, let's start with the main topic. Kruskal's Algorithm is used to find the minimum spanning tree for a connected weighted graph. The main target of the algorithm is to find the subset of edges by using which we can traverse every vertex of the graph. It follows the greedy approach that finds an optimum solution at every stage instead of focusing on a global optimum. How does Kruskal's algorithm work?In Kruskal's algorithm, we start from edges with the lowest weight and keep adding the edges until the goal is reached. The steps to implement Kruskal's algorithm are listed as follows -
The applications of Kruskal's algorithm are -
Example of Kruskal's algorithmNow, let's see the working of Kruskal's algorithm using an example. It will be easier to understand Kruskal's algorithm using an example. Suppose a weighted graph is - 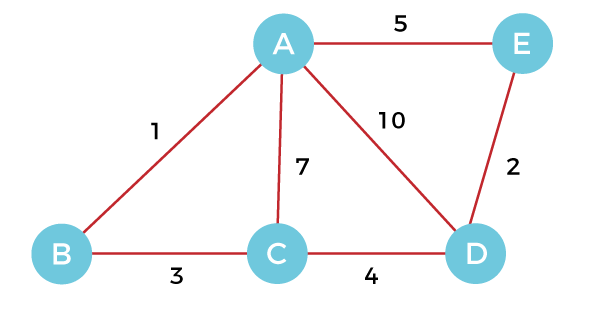
The weight of the edges of the above graph is given in the below table -
Now, sort the edges given above in the ascending order of their weights.
Now, let's start constructing the minimum spanning tree. Step 1 - First, add the edge AB with weight 1 to the MST. 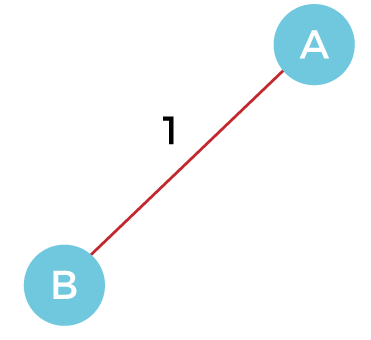
Step 2 - Add the edge DE with weight 2 to the MST as it is not creating the cycle. 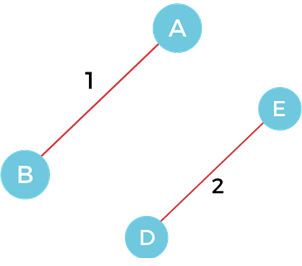
Step 3 - Add the edge BC with weight 3 to the MST, as it is not creating any cycle or loop. 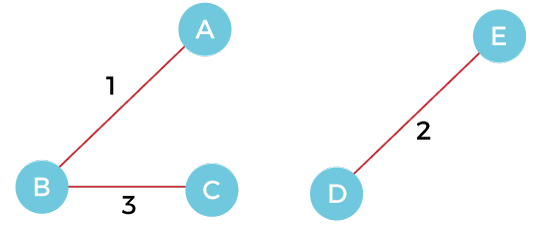
Step 4 - Now, pick the edge CD with weight 4 to the MST, as it is not forming the cycle. 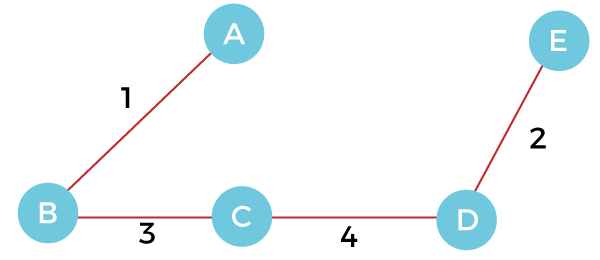
Step 5 - After that, pick the edge AE with weight 5. Including this edge will create the cycle, so discard it. Step 6 - Pick the edge AC with weight 7. Including this edge will create the cycle, so discard it. Step 7 - Pick the edge AD with weight 10. Including this edge will also create the cycle, so discard it. So, the final minimum spanning tree obtained from the given weighted graph by using Kruskal's algorithm is - 
The cost of the MST is = AB + DE + BC + CD = 1 + 2 + 3 + 4 = 10. Now, the number of edges in the above tree equals the number of vertices minus 1. So, the algorithm stops here. AlgorithmComplexity of Kruskal's algorithmNow, let's see the time complexity of Kruskal's algorithm.
Implementation of Kruskal's algorithmNow, let's see the implementation of kruskal's algorithm. Program: Write a program to implement kruskal's algorithm in C++. Output 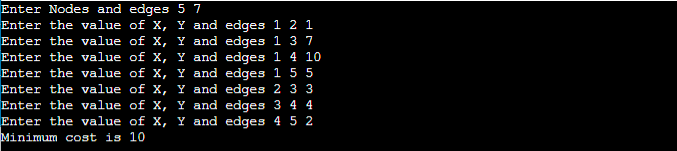
So, that's all about the article. Hope the article will be helpful and informative to you.
Next TopicLinear Search
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










