LALR (1) Parsing:LALR refers to the lookahead LR. To construct the LALR (1) parsing table, we use the canonical collection of LR (1) items. In the LALR (1) parsing, the LR (1) items which have same productions but different look ahead are combined to form a single set of itemsLALR (1) parsing is same as the CLR (1) parsing, only difference in the parsing table. ExampleLALR ( 1 ) GrammarAdd Augment Production, insert '•' symbol at the first position for every production in G and also add the look ahead. I0 State: Add Augment production to the I0 State and Compute the ClosureL I0 = Closure (S` → •S) Add all productions starting with S in to I0 State because "•" is followed by the non-terminal. So, the I0 State becomes I0 = S` → •S, $ Add all productions starting with A in modified I0 State because "•" is followed by the non-terminal. So, the I0 State becomes. I0= S` → •S, $ I1= Go to (I0, S) = closure (S` → S•, $) = S` → S•, $ Add all productions starting with A in I2 State because "•" is followed by the non-terminal. So, the I2 State becomes I2= S → A•A, $ I3= Go to (I0, a) = Closure ( A → a•A, a/b ) Add all productions starting with A in I3 State because "•" is followed by the non-terminal. So, the I3 State becomes I3= A → a•A, a/b Go to (I3, a) = Closure (A → a•A, a/b) = (same as I3) I4= Go to (I0, b) = closure ( A → b•, a/b) = A → b•, a/b Add all productions starting with A in I6 State because "•" is followed by the non-terminal. So, the I6 State becomes I6 = A → a•A, $ Go to (I6, a) = Closure (A → a•A, $) = (same as I6) I7= Go to (I2, b) = Closure (A → b•, $) = A → b•, $ If we analyze then LR (0) items of I3 and I6 are same but they differ only in their lookahead. I3 = { A → a•A, a/b I6= { A → a•A, $ Clearly I3 and I6 are same in their LR (0) items but differ in their lookahead, so we can combine them and called as I36. I36 = { A → a•A, a/b/$ The I4 and I7 are same but they differ only in their look ahead, so we can combine them and called as I47. I47 = {A → b•, a/b/$} The I8 and I9 are same but they differ only in their look ahead, so we can combine them and called as I89. I89 = {A → aA•, a/b/$} Drawing DFA: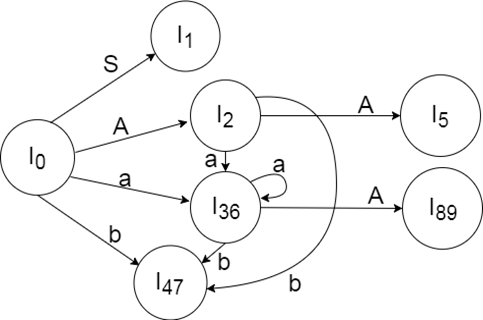
LALR (1) Parsing table: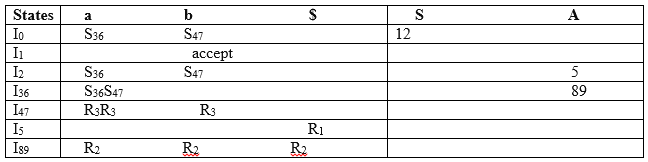
Next TopicAutomatic Parser Generator
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










