Largest Independent Set in Java

A binary tree is given to us. Our task is to find the size of the largest independent set of the given binary tree. An independent set of a binary tree consists of only those nodes of the binary tree that are not connected directly with each other. In other words, for any two nodes in the set, there has to be at least one node between them.

Example:

Input:

For the following binary tree: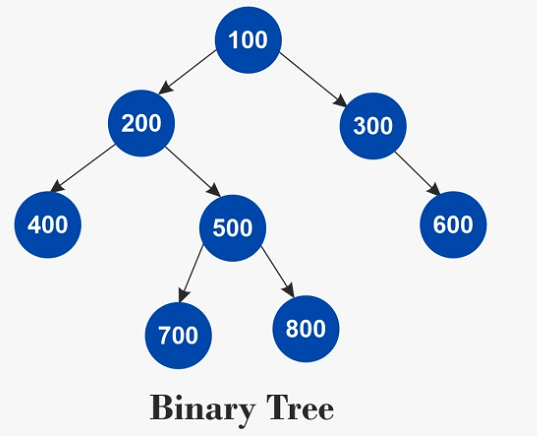

The largest independent set is {100, 400, 600, 700, 800} as these nodes are not adjacent to each other. Its size is 5. Hence, the output is 5.

Approach: Using Recursion

The approach is simple. A node of the given binary tree can be part of the solution or can not be part of the solution. We can have recursive calls based on these two conditions. One recursive call includes the node, and the other excludes the node in the solution. The following implementation shows the same.

FileName: LIS.java

// The following program implements the LIS using brute force 
// or naive recursive approach.
public class LIS 
{

// a method that computes the maximum
// between two numbers p and q
public int findMax(int p, int q)
{
return (p > q) ? p : q;
}


// a binary tree that has two pointers and a variable v
// v stores the data, and lNode and rNode are the two pointers that point
// to the left and right nodes of the binary tree
static class BTNode
{
int v;
BTNode lNode;
BTNode rNode;
};

// A method that returns the size of the Largest Independent Set
// using the given binary tree whose root is rtNode
// binary tree
public int computeLISSize(BTNode rtNode)
{
if (rtNode == null)
{
return 0;
}

// Calculate size excluding the current node
int excludeSiz = computeLISSize(rtNode.lNode) +
computeLISSize(rtNode.rNode);

// Calculate size including the current node
int includeSiz = 1;
if (rtNode.lNode != null)
{
includeSiz = includeSiz + computeLISSize(rtNode.lNode.lNode) + computeLISSize(rtNode.lNode.rNode);
}

if (rtNode.rNode != null)
{
includeSiz = includeSiz + computeLISSize(rtNode.rNode.lNode) + computeLISSize(rtNode.rNode.rNode);
}

// Returning the maximum from includeSiz and excludeSiz 
// by invoking the findMax method.
return findMax(includeSiz, excludeSiz);
}

// A method for creating the binary node
static BTNode createNewNode( int v )
{
BTNode tmp = new BTNode();
tmp.v = v;
tmp.lNode = null;
tmp.rNode = null;
return tmp;
}

// Driver Code
public static void main(String args[]) 
{
// Constructing the binary tree 
//  as per the diagram given above.
BTNode rt = createNewNode(100);
rt.lNode = createNewNode(200);
rt.lNode.lNode = createNewNode(400);
rt.lNode.rNode = createNewNode(500);
rt.lNode.rNode.lNode = createNewNode(700);
rt.lNode.rNode.rNode = createNewNode(800);
rt.rNode = createNewNode(300);
rt.rNode.rNode = createNewNode(600);

// creating an object of the class LIS
LIS obj = new LIS();

// invoking the method computeLISSize()
int ans = obj.computeLISSize(rt);

System.out.println("The size of the Largest Independent Set is: " + ans);
}
}

Output:

The size of the Largest Independent Set is: 5

Complexity Analysis: In the above program, each recursive call leads to two recursive (one for excluding, another for including the element in the solution) calls. Therefore, the time complexity of the program is O(2ⁿ), where n is the total number of nodes present in the binary tree. Note that it is the exponential time complexity.

The time complexity of the program is very high as it is exponential. Therefore, for handling the larger inputs, the above program is not suitable, and hence it is required to do some optimization.

Approach: Using Recursion With Memoization

The above program is computing many subproblems again and again, and that leads to higher time complexity. For example, A node with the value 500 is computed for the nodes with the values 100 and 200, where the node with the value 500 acts as a grandchild of the node with value 100 and as a child of the node of value 200. Therefore, we need to build the solution in a bottom-up manner and store the solution of the subproblems so that it is not getting computed again and again.

Let's observe the modified form of the above program.

FileName: LIS1.java

public class LIS1 
{

// a method that computes the maximum
// between two numbers p and q
public int findMax(int p, int q)
{
return (p > q) ? p : q;
}


// a binary tree that has two pointers and a variable v
// v stores the data, and lNode and rNode are the two pointers that point
// to the left and right nodes of the binary tree
// We have also added a variable maxSize for storing the size of the largest 
// independent subset computed at that point
static class BTNode
{
int v;
int maxSize;
BTNode lNode;
BTNode rNode;
};

// A method that returns the size of the Largest Independent Set
// using the given binary tree whose root is rtNode
// binary tree
public int computeLISSize(BTNode rtNode)
{
if (rtNode == null)
{
return 0;
}

if (rtNode.maxSize != 0)
{
return rtNode.maxSize;
}

if (rtNode.lNode == null && rtNode.rNode == null)
{
return rtNode.maxSize = 1;
}

// Calculate size excluding the current node
int excludeSiz = computeLISSize(rtNode.lNode) +
computeLISSize(rtNode.rNode);

// Calculate size including the current node
int includeSiz = 1;
if (rtNode.lNode != null)
{
includeSiz = includeSiz + computeLISSize(rtNode.lNode.lNode) + computeLISSize(rtNode.lNode.rNode);
}
if (rtNode.rNode != null)
{
includeSiz = includeSiz + computeLISSize(rtNode.rNode.lNode) + computeLISSize(rtNode.rNode.rNode);
}

// Storing the maximum from includeSiz and excludeSiz 
// by invoking the findMax method so that it can be used further
return rtNode.maxSize = findMax(includeSiz, excludeSiz);
}

// A method for creating the binary node
static BTNode createNewNode( int v )
{
BTNode tmp = new BTNode();
tmp.v = v;
tmp.maxSize = 0;
tmp.lNode = null;
tmp.rNode = null;
return tmp;
}

// Driver Code
public static void main(String argvs[]) 
{
// Constructing the binary tree 
//  as per the diagram given above.
BTNode rt = createNewNode(100);
rt.lNode = createNewNode(200);
rt.lNode.lNode = createNewNode(400);
rt.lNode.rNode = createNewNode(500);
rt.lNode.rNode.lNode = createNewNode(700);
rt.lNode.rNode.rNode = createNewNode(800);
rt.rNode = createNewNode(300);
rt.rNode.rNode = createNewNode(600);

// creating an object of the class LIS1
LIS1 obj = new LIS1();

// invoking the method computeLISSize()
int ans = obj.computeLISSize(rt);

System.out.println("The size of the Largest Independent Set is: " + ans);
}
}

Output:

The size of the Largest Independent Set is: 5

Complexity Analysis: Because of the memorization, the time complexity of the program is O(n), where n is the total number of nodes present in the binary tree.

Next TopicLongest Subarray With All Even or Odd Elements in Java

← prev next →