Lazy Propagation in Segment TreeIn the last post, the segment tree was presented along with a range sum problem example. We explained lazy propagation using the same "Sum of specified Range" problem. 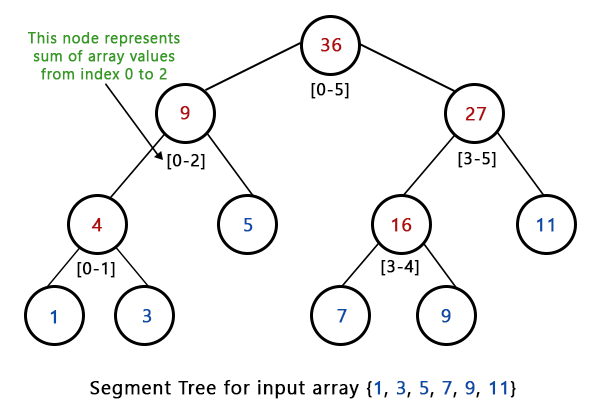
How does the Simple Segment Tree update function?The update method was used in the last lesson to change just one value in an array. Due to the possibility that several segment tree nodes have a single array element in their ranges, it is important to be aware that a single value update in an array may result in multiple updates in the segment tree. This post's simple reasoning is shown below. 1) Begin at the segment tree's root. 2) Return if the array index that has to be modified is outside the current node's range. 3) Update the current node and repeat for children if not. The code from the previous post is shown here. C++ CodeThe application of the aforementioned strategy is seen below: What if a number of array indexes have updates?Add 10, for instance, to each element in the array with an index between 2 and 7. For every index from 2 to 7, the aforementioned update has to be called. By creating a function called updateRange() that updates nodes as necessary, we can avoid making numerous calls. C++ CodeThe application of the aforementioned strategy is seen below: Lazy Propagation is an optimization for speeding up range updates.We can delay some updates when there are multiple updates and updates are being performed on a range (avoiding recursive calls in update) and do such updates just as needed. Please keep in mind that a node in a segment tree stores or symbolises the outcome of a query for a variety of indexes. Additionally, if the update operation's range includes this node, all of its descendants must likewise be updated. Consider, for instance, the node with value 27 in the picture above. This node contains the sum of values at indexes ranging from 3 to 5. We must update both this node and all of its descendants if our update query covers the range 2 to 5. By storing this update information in distinct nodes referred to as lazy nodes or values, we use lazy propagation to update only the node with value 27 and delay updates to its descendants. We make an array called lazy [] to stand in for the lazy node. The size of lazy [] is the same as the array used to represent the segment tree in the code following, which is tree []. The goal is to set all of lazy [elements ]'s to 0. There are no pending changes on segment tree node I if lazy[i] has a value of 0. A non-zero value for lazy[i] indicates that before doing any queries on node I in the segment tree, this sum needs to be added to the node. Here is an updated updating technique. Has the Query Function changed as well?If a query is sent to a node that hasn't been updated yet, there can be issues because we adjusted update to postpone its activities. Therefore, we also need to alter the query method we used in the previous post, getSumUtil. The getSumUtil() now determines whether an update is pending before updating the node. Once it confirms that any pending updates have been made, it functions similarly to the previous getSumUtil (). The programmes below show how Lazy Propagation works. C++ CodeThe application of the aforementioned strategy is seen below: Output: Sum of values in given range = 15 Updated sum of values in given range = 45 Time Complexity: O(n) Auxiliary Space: O(MAX)
Next TopicSegment Tree - Range Minimum Query
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










