Least Common MultipleIn arithmetic, Least Common Multiple (LCM) of two or more numbers is the least positive number that can be divided by both the numbers, without leaving the remainder. It is also known as Lowest Common Multiple (LCM), Least Common Denominator, and Smallest Common Multiple. It is denoted by LCM (a, b) or lcm (a, b) where a and b are two integers. It is used when we add, subtract, or compare the fractions. While we perform addition or subtraction of the fractions, we find the LCM of the denominators and then solve the fractions. The LCM of the denominators is known as the Least Common Denominator (LCD). Properties of LCM
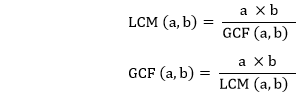
How to Find LCMThere are three method to find the LCM, are as follows:
Using Table MethodIt is a simple method and works for any number of numbers. Follow the steps given below to find the LCM.
Let's understand it through examples. Example 1: Find the LCM of 8 and 10. Solution: 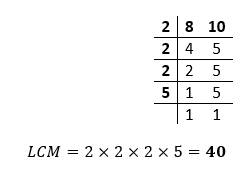
Hence, the LCM of 8 and 10 is 40. Example 2: Find the LCM of 60 and 282. Solution: 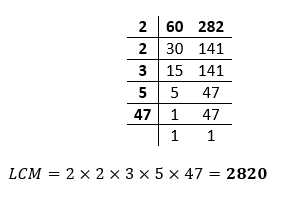
Hence, the LCM of 60 and 282 is 2820. Example 3: What is the LCM of 20, 28, and 35. Solution: 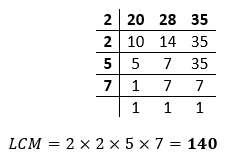
Hence, the LCM of 20, 28, and 35 is 140. Example 4: Find the LCM of 120, 144, 160, and 180. Solution: 
Hence, the LCM of 120, 144, 160, and 180 is 1440. Example 5: Find the LCM of 64, 72, 96, and 108. Solution: 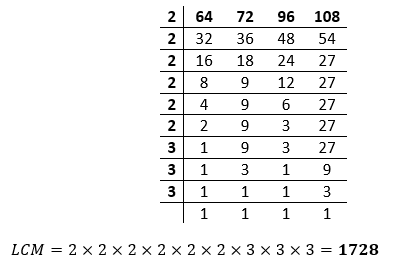
Hence, the LCM of 64, 72, 96, and 108 is 1728. Using the Greatest Common Divisor (GCD) MethodWe can also calculate the LCM by using the GCD. The formula for LCM using the GCD is: 
Greatest Common Divisor: It is the highest number that completely divides two or more numbers. It is abbreviated for GCD. It is also known as the Greatest Common Factor (GCF) or the Highest Common Factor (HCF). How to Find GCDFollow the steps given below to find the GCD:
Let's understand it through examples. Example 6: Find the LCM of 8 and 10. Solution: According to the formula that we have learned above: 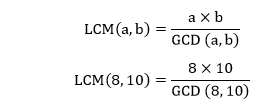
First, we find the GCD of 8 and 10. Factors of 8: 1, 2, 4, 8 Factors of 10: 1, 2, 5, 10 Common Factors: 1, 2 Greatest Common Divisor: 2 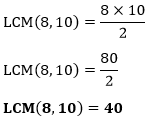
Hence, the LCM of 8 and 10 is 40. Example 7: Find the LCM of 11 and 42. Solution: According to the formula that we have learned above: 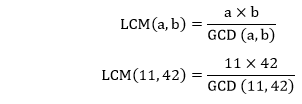
First, we find the GCD of 11 and 42. Factors of 11: 1, 11 Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42 Common Factors: 1 Greatest Common Divisor: 1 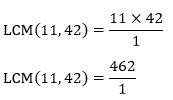
LCM(11,42)=462 Hence, the LCM of 11 and 42 is 462. Example 8: Find the LCM of 64 and 112. Solution: According to the formula that we have learned above: 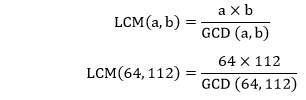
First, we find the GCD of 64 and 112. Factors of 64: 1, 2, 4, 8, 16, 32, 64 Factors of 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, 112 Common Factors: 1, 2, 4, 7, 8, 16 Greatest Common Divisor: 16 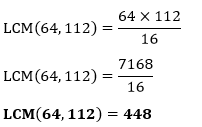
Hence, the LCM of 64 and 112 is 448. Using Prime Factorization MethodFollow the steps to find the LCM using the prime factorization method.
Note: When we write the factors in the form of is called exponential form, and the process is known as factorization using exponents.Let's understand through examples. Example 9: Find the LCM of 17 and 28. Solution: Prime factor of 17: 17 In exponential form: Prime factor of 17: 171 Hence, the LCM of 17 and 28 is 476. Example 10: What is the LCM of 35 and 78. Solution: Prime factor of 35: 5×7 In exponential form: Prime factor of 35: 51×71 Hence, the LCM of 35 and 78 is 2730. Example 11: Find the LCM of 223 and 432. Solution: Prime factor of 223: 223 In exponential form: Prime factor of 223: 2231 Hence, the LCM of 223 and 432 is 96336. Example 12: Find the LCM of 12, 23, and 29. Solution: Prime factor of 12: 2 × 2 × 3 In exponential form: Prime factor of 12: 22×31 Hence, the LCM of 12, 23, and 29 is 8004. Using Multiples of NumbersIt is a very lengthy method, so it is not usually used. Follow the steps given below to find the LCM using multiples of numbers.
Let's understand it through examples. Example 13: What is the LCM of 12, 9, and 33. Solution: Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135, 144, 153, 162, 171, 180, 189, 198, 207, 216, 225, 234, 243, 252, 261, 270, 279, 288, 297, 306, 315, 324, 333, 342, 351, 360, 369, 378, 387, 396, 405, 414 Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204, 216, 228, 240, 252, 264, 276, 288, 300, 312, 324, 336, 348, 360, 372, 384, 396, 408, 420 Multiples of 33: 33, 66, 99, 132, 165, 198, 231, 264, 297, 330, 363, 396, 429, 462 Hence, the LCM of 9, 12, and 33 is 396. Example 14: What is the LCM of 15 and 16. Solution: Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, 270 Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272 LCM (15,16)=240 Hence, the LCM of 15 and 16 is 240. LCM of FractionsWe can also find the LCM of the fractions by using the following formula: 
Example 15: What is the LCM of Solution: LCM of numerators: 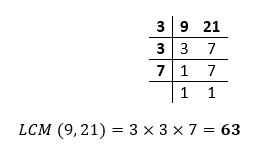
HCF of denominators: Factors of 2: 1, 2 HCF: 2 Putting the values in the formula, we get: 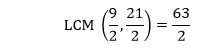
Hence, the LCM of Example 16: What is the LCM of Solution: LCM of numerators: 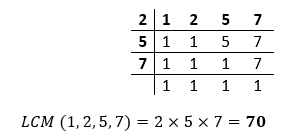
HCF of denominators: Factors of 2: 1, 2 Factors of 3: 1, 3 Factors of 4: 1, 2, 4 Factors of 5: 1, 5 HCF: 1 Putting the values in the formula, we get: 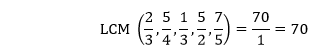
Hence, the LCM of Example 17: What is the LCM of Solution: LCM of numerators: 
HCF of denominators: Factors of 9: 1, 3, 9 Factor of 1: 1 Factors of 5: 1, 5 HCF: 1 Putting the values in the formula, we get: 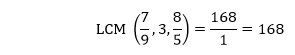
Hence, the LCM of
Next TopicPerfect Squares
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





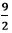 and
and 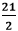 .
.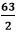 .
.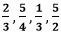 and
and 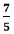 .
.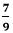 ,3, and
,3, and 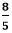 .
.




