Limit Definition

In mathematics, limits play a significant role in calculus and other areas of analysis. Limits provide a way of describing the behavior of a function as the input variable approaches a certain value or infinity. The concept of limits is essential for understanding the definition and properties of derivatives, integrals, continuity, and convergence of sequences and series.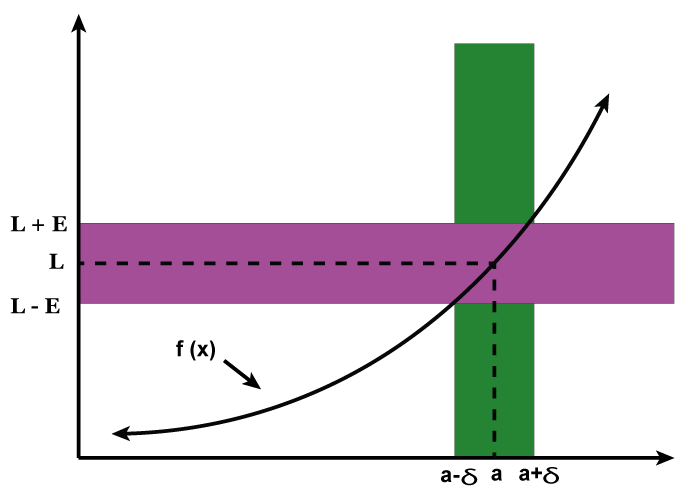

Definition of a Limit

Formally, the limit of a function f(x) as x approaches a particular value a is defined as follows:

Lim_x→a f(x) = L

This definition states that as x gets closer to a, the value of f(x) gets closer to L. If L exists, then the function is said to be continuous at a.

One-sided Limits

In some cases, it may not be possible to approach a point a from both sides. In such cases, we use one-sided limits. The left-hand limit of a function f(x) as x approaches a from the left is defined as:

Lim_x→a− f(x)

Similarly, the right-hand limit of a function f(x) as x approaches a from the right is defined as:

Lim_x→a+ f(x)

If both the left-hand and right-hand limits exist and are equal, then the limit exists.

Properties of Limits

The following are some of the important properties of limits:

1. Algebraic Properties: Limits can be added, subtracted, multiplied, and divided like any other algebraic expressions. That is, if Lim_x→a f(x) and Lim_x→a g(x) exist, then the following limits also exist:

1. Lim_x→a [f(x) + g(x)] = Lim_x→a f(x) + Lim_x→a g(x)
2. Lim_x→a [f(x) - g(x)] = Lim_x→a f(x) - Lim_x→a g(x)
3. Lim_x→a [f(x) × g(x)] = Lim_x→a f(x) × Lim_x→a g(x)
4. Lim_x→a [f(x) / g(x)] = (Lim_x→a f(x)) / (Lim_x→a g(x)) provided Lim_x→a g(x) ≠ 0

2. Squeeze theorem: If f(x) ≤ g(x) ≤ h(x) for all x in some interval containing a (except possibly at a), and Lim_x→a f(x) = Lim_x→a h(x) = L, then Lim_x→a g(x) also exists and is equal to L.

3. The limit of a constant function: If f(x) = c for all x, then Lim_x→a f(x) = c.

4. The limit of an identity function: If f(x) = x, then Lim_x→a f(x) = a.

5. The limit of a power function: If f(x) = x^n, where n is a positive integer, then Lim_x→a f(x) = a^n.

6. The limit of a sum/difference of functions: If f(x) and g(x) have limits as x approaches a, then the limit of their sum/difference also exists and is equal to the sum/difference of their limits.

7. The limit of a product of functions: If f(x) and g(x) have limits as x approaches a, then the limit of their product also exists and is equal to the product of their limits.

8. The limit of a quotient of functions: If f(x) and g(x) have limits as x approaches a and Lim_x→a g(x) ≠ 0, then the limit of their quotient also exists and is equal to the quotient of their limits.

Continuity

Continuity is a fundamental concept in calculus and analysis. A function f(x) is said to be continuous at a point a if the limit of f(x) as x approaches a exists and is equal to f(a). In other words, the function has no sudden jumps or breaks at a. If a function is not continuous at a point, we say that it has a discontinuity at that point.

There are three types of discontinuities:

1. Removable discontinuity: A removable discontinuity occurs when a function has a hole at a point a. In other words, the function is undefined at a, but there exists a limit at that point. We can remove the discontinuity by redefining the function at a single point.
2. Jump discontinuity: A jump discontinuity occurs when the left-hand limit and right-hand limit of a function at a point a exist, but they are not equal. In other words, the function "jumps" from one value to another at a.
3. 5Infinite discontinuity: An infinite discontinuity occurs when a function has a vertical asymptote at a point a. In other words, the function approaches positive or negative infinity as x approaches a.

Derivatives

The derivative of a function is one of the most important concepts in calculus. The derivative measures the rate at which a function changes as the input variable changes. Formally, the derivative of a function f(x) at a point a is defined as:

f'(a) = Lim_x→a [f(x) - f(a)] / (x - a)

If this limit exists, then f(x) is said to be differentiable at a. Geometrically, the derivative represents the slope of the tangent line to the graph of f(x) at the point (a, f(a)).

The derivative has many applications in mathematics and science, including optimization, physics, and engineering. For example, the derivative can be used to find the maximum or minimum value of a function, to determine the velocity or acceleration of an object, or to model the behavior of a population.

Integrals

The integral is another fundamental concept in calculus. The integral measures the area under the curve of a function between two points. Formally, the definite integral of a function f(x) over an interval [a, b] is defined as:

Integral_a^b f(x) dx = Lim_n→∞ [∑i=1^n f(xi) Δx]

where Δx = (b - a) / n and xi = a + iΔx for i = 1, 2, ..., n. Geometrically, the integral represents the area of the region bounded by the graph of f(x), the x-axis, and the vertical lines x = a and x = b.

The integral has many applications in mathematics and science, including geometry, physics, and engineering. For example, the integral can be used to calculate the volume of a solid, to find the work done by a force, or to compute the probability of an event.

Conclusion

In conclusion, limits are an essential concept in mathematics, especially in calculus and analysis. They provide a way of describing the behavior of a function as the input variable approaches a certain value or infinity. The concept of limits leads to the definition and properties of derivatives, integrals, continuity, and convergence of sequences and series. Limits play a crucial role in many areas of mathematics and science and have numerous practical applications in engineering, physics, and other fields.