Math DefinitionWhat is Mathematics?We all have studied mathematics from a very young age and know that it is a vast and very intriguing subject, but have you ever thought about how much of an impact mathematics has had on our lives and society as a whole? Simply, the field of mathematics could be defined as the study of numbers, shapes, and quantities. In mathematics, we deal with the logical and systematic manipulation of abstract concepts, such as numbers, quantities, shapes, and patterns. It involves using symbols, formulas, and equations to describe and solve problems in various areas. Mathematics is involved in so many things we do and use every day, like counting our money, building cool stuff, making technologies work, and even creating amazing art. The best thing about math is that it helps us solve our problems by making smart choices using logic and precision. For thousands of years, mathematics has played a pivotal role in human history, contributing to some of the most profound discoveries and many groundbreaking inventions. It has an enduring presence across various fields of knowledge, making it a cornerstone of modern civilization. You can easily trace back the history of mathematics to ancient civilizations such as the Greeks and the Romans. The groundwork of the modern mathematics that we study today has been laid down by these ancients. The Romans used applied mathematics to solve many practical problems, such as measuring land, building structures, bookkeeping, creating lunar and solar calendars, and even in art and craft. In contrast, Greeks contributed mainly to theoretical mathematics. The contributions made by the Greeks to theoretical mathematics had a lasting impact on the subject, and their ideas and concepts have stood the test of time and are still in use today. Pythagoras, a famous Greek mathematician, is considered one of the most influential figures in the history of mathematics. Pythagorean Theorem, developed by him, is one of the most fundamental concepts in the field of geometry. This theorem describes the relationship between the sides of a right-angled triangle and has numerous practical applications in fields ranging from architecture to engineering. Euclid, another renowned Greek mathematician, is famous for his book, the Elements. This book is a treasure trove of geometric concepts that have laid the foundation for mathematics as we know it today. In this book, Euclid outlined many of the basic principles of geometry that we have been using to this day. Modern mathematics is divided into several different fields of study that include algebra, geometry, calculus, and statistics. Each branch is like a different part of math that helps us solve different problems. Algebra focuses on the manipulation of equations and the analysis of mathematical structures, while geometry is concerned with the study of shapes and their properties. Calculus deals with the rates of change and the interconnection between the functions. Meanwhile, statistics is all about gathering, analyzing, and interpreting data. Mathematics is important in many areas, like physics, engineering, and computer science. Application of its concepts is crucial in scientific and engineering fields as it enables professionals to solve complex problems and develop innovative technologies such as cars, robots, and computers. Without mathematics, many of the technological advancements we enjoy today would not be possible. For example, the laws of motion and gravity discovered by Sir Isaac Newton are based on principles of mathematics, as are the equations used to design bridges and buildings. People specializing in finance and economics also heavily rely on mathematics and their various tools. Economists use statistical models to study how people and companies behave, while financial analysts use mathematical models to make predictions about the stock market and decide where to invest. In conclusion, mathematics is a vast and fascinating subject that has played a vital role in shaping our world. From the early days of counting and measuring to the modern-day applications of calculus, statistics, and algebra, mathematics has been integral to our daily lives. In this article, we will explore some basic tools of mathematics, their importance, and some of their most interesting applications. Whether you are a student, a professional, or simply someone who is curious about the world around you, this article will provide you with a solid foundation to understand and appreciate the beauty of mathematics. So, let's get started! Mixed FractionsMixed fractions, also known as mixed numbers, are a common type of mathematical expression we use in our everyday life. Mixed fractions are numbers that have a whole number and a fraction combined. We express the mixed fraction in the form a b/c, where a is the whole number, b is the numerator of the fraction, and c is the denominator of the fraction. For example, 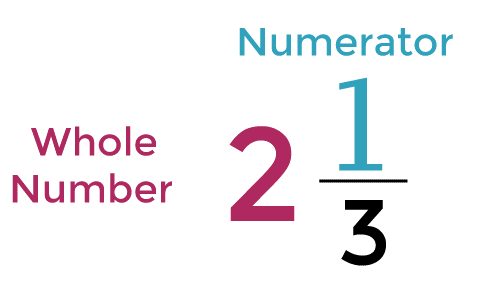
Mixed fractions are useful in many real-life situations where we need to represent quantities that are not whole numbers but are still greater than one, such as, when measuring ingredients for a recipe or calculating distances on a map. We also often use mixed fractions in cooking and baking, where ingredients are generally measured in fractions of a unit, such as cups or tablespoons. For example, while buying groceries, we may ask the shopkeeper to give us Mixed fractions are also useful in representing measurements in other fields, such as construction or engineering. For example, a construction project might require a piece of lumber that is Conversion between Mixed Fractions and Improper FractionsIf we want to turn a number that is a mixed fraction, for example,
So if we convert the mixed fraction To put it in other words, we take the whole number, turn it into a fraction by putting it over the denominator, and then add that to the original fraction. Let us take another example, to convert the mixed fraction 2 1/3 to an improper fraction, we will proceed as below: 2 x 3 = 6 6 +1 = 7 So, Conversely, if we want to convert an improper fraction, such as 5/3 to a mixed fraction, we must follow the following steps.
Let us take another example, to convert the improper fraction 7/3 to a mixed fraction, we will proceed as below: 7 � 3 = 2, remainder 1 So, 7/3 is equivalent to Properties of Mixed Fractions:
In conclusion, mixed fractions are a useful and common mathematical expression used to represent quantities that are not whole numbers but are still greater than one. They can be converted to improper fractions and back again and can be used in various fields, such as cooking, construction, and engineering. Understanding how to work with mixed fractions is an important skill in everyday life and many professional fields. Standard DeviationStandard deviation is an important statistical tool we often use to describe how much a given set of data varies. It is a way to find out how spread out a group of numbers is. It helps you see how much the numbers in a set are different from each other. It is a measure of how much the data deviates from the mean or average of the data set. We express the standard deviation in the same units as the given data. This fundamental tool of statistics is used in many different fields, including science, engineering, finance, and economics. To better understand standard deviation, it is important that we first understand what is meant by variability in a given data set. Variability refers to how spread out the data is from the mean or central value. To put it simply, if a data set has high variability, it means that the values are widely spread out. In contrast, a low variability indicates that the values are closer to the mean or average value. 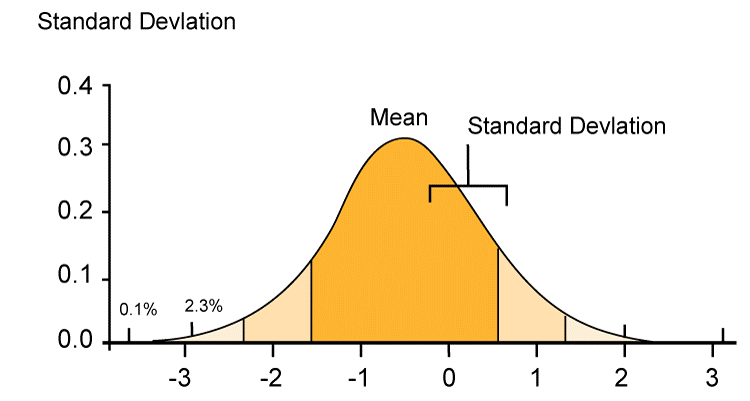
We use standard deviation to measure this variability. To calculate the standard deviation we need to find the square root of the variance. To calculate the variance, we first find the average (mean) of the data set. Then, for each number in the dataset, we subtract the mean from that number, square the result, and add it to a running total. Finally, you divide the total by the number of data points. Mathematically this is represented as: ? = ?(?(xi - ?)� / n) Where:
We use this statistical tool in many ways, one of which is hypothesis testing. In hypothetical testing, we determine the statistical significance of the difference between two groups or sets of data. Let us take an example, in a clinical trial, the standard deviation can be used to determine whether a new treatment is significantly different from a control group. We also use this statistical tool in finance and risk management. We use it to measure whether a stock or a portfolio of stocks will grow or decline at a particular time, which is an important consideration for investors. A higher standard deviation implies higher risk and lower predictability of returns. In conclusion, a standard deviation is a vital tool in statistics that measures the variability of a data set. It tells us how spread out the data is from the mean or central value. It is used in many different fields, including science, engineering, finance, and economics. Understanding standard deviation is essential for making informed decisions and drawing accurate conclusions from data sets. Straight AngleIn geometry, one of the most important concepts is a straight angle. We can define a straight angle simply as an angle that measures exactly 180 degrees and is as big as a straight line, hence this angle is also known as a "line angle". When we divide a straight line into two halves, each half measures 90 degrees and is called a right angle. Therefore, a straight angle can be made by joining two right angles. One of the most critical properties of a straight angle is that it is always the sum of two adjacent angles, whose measures add up to 180 degrees. For example, if we place a ladder against a wall, it will form two adjacent angles with the wall, the sum of these two angles is 180�, and we also call such a pair of adjacent angles, linear pair. 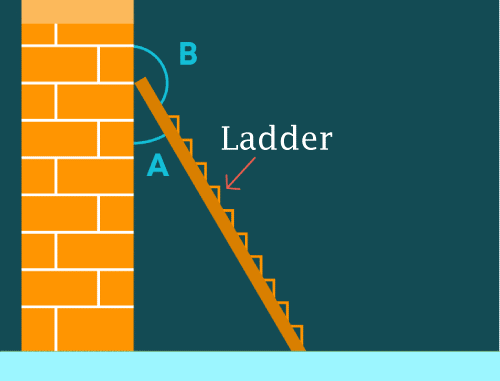
Another important property of a straight angle is that it reverses the direction of a point. It means that if we have a point P located at the vertex of the straight angle, and we rotate one of the rays of the angle by 180 degrees around P, then the new position of the ray will be in the opposite direction from its original position. We use the concept of a straight angle in many different areas of mathematics and physics. For example, Trigonometry relies on the concept of a straight angle to establish the unit circle and determine the sine and cosine functions. Similarly, physics employs this concept to explain the behavior of light since light travels in straight lines. In conclusion, the concept of straight angles may be simple, but of real importance in both mathematics and physics, because it sets the groundwork for a lot of other concepts. Understanding the properties of a straight angle is essential for anyone studying mathematics or physics, and it is a concept that is frequently used in everyday life.
Next TopicPerimeter definition
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





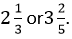
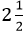 kilograms of flour, which is equivalent to 2 kilograms and 500 grams.
kilograms of flour, which is equivalent to 2 kilograms and 500 grams.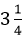 inches long, or an engineering problem might involve a bolt that is
inches long, or an engineering problem might involve a bolt that is 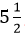 millimeters in diameter.
millimeters in diameter.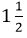 into an improper fraction, we have to follow the following steps:
into an improper fraction, we have to follow the following steps: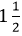 to an improper fraction, we get
to an improper fraction, we get 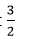
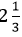 is equivalent to
is equivalent to 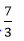
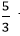 to a mixed fraction, we get
to a mixed fraction, we get 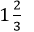
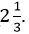 .
.




