MATLAB Trapezoidal RuleConsider the function y=f(x) for the interval a≤x≤b, shown in figure: 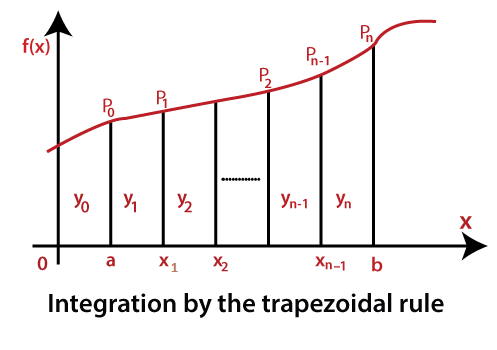
To evaluate the definite integral, The total area is: 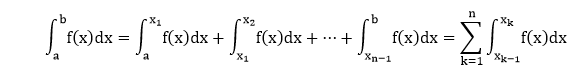
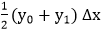 plus the area of the trapezoid x1 P1 P2 x2 that is equal to plus the area of the trapezoid x1 P1 P2 x2 that is equal to 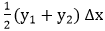 , and so on. Then, the trapezoidal approximation becomes , and so on. Then, the trapezoidal approximation becomes
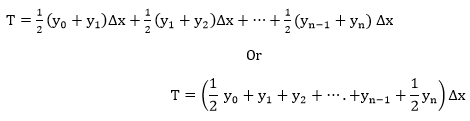
ExampleUsing the trapezoidal rule with n=4, estimate the cost of the definite integral 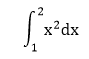
Compare with the exact value and evaluate the percent error. Solution: The exact value of this integral is 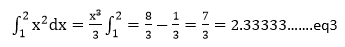
For the trapezoidal rule approximation, we have 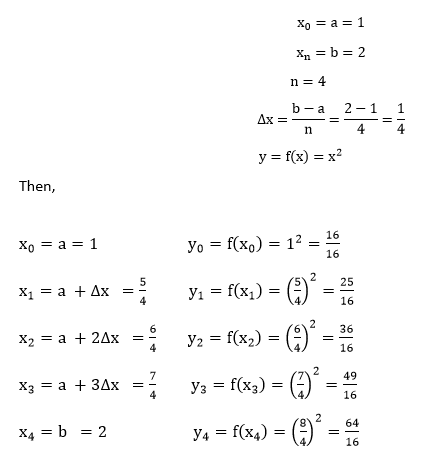
and by substitution into an equation 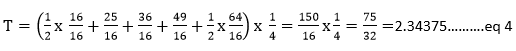
From equation 3 and equation 4, we find that the percent error is 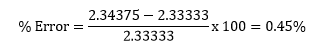
Next TopicMATLAB Trapz
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





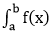 dx, we divide the interval a≤x≤b into subintervals each of length
dx, we divide the interval a≤x≤b into subintervals each of length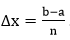 . Then, the number of points between x0=a,and xn=b is x1=a+∆x,x2=a+2∆x,…xn-1=a+(n-1)∆x. Therefore, the integral from a to b is the sum of the integrals from a to x1, from x1 to x2 and so on, and finally from xn-1 to b.
. Then, the number of points between x0=a,and xn=b is x1=a+∆x,x2=a+2∆x,…xn-1=a+(n-1)∆x. Therefore, the integral from a to b is the sum of the integrals from a to x1, from x1 to x2 and so on, and finally from xn-1 to b.




