Matrix MultiplicationIn mathematics, matrix multiplication is different from the multiplication that we perform, generally. It is a binary operation that performs between two matrices and produces a new matrix. In this section, we will learn matrix multiplication, its properties, along with its examples. While we do addition or subtraction of matrices, we add or subtract the elements matching with the positions. But in matrix multiplication, we do not so. Instead of it, we perform the dot product of the rows and columns. Dot Product: It is the sum of the product of the matching entries of the two sequences of the numbers. Note: While dealing with the matrix multiplication, remember that the number of columns in the first matrix must be equals to the number of rows in the second matrix. If the condition is not satisfied, the matrix multiplication is not possible.In matrix multiplication, it is not necessary that both matrices must be a square matrix, as in addition and subtraction. Suppose we have a matrix A of m×n dimensions and a matrix B of n×k dimensions, then the resultant matrix will be of m×k dimensions. 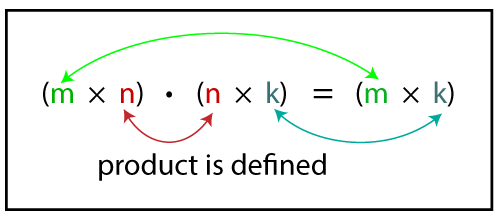
Let's understand it through an example. Suppose we have two matrices A and B of dimensions 2×3 and 3×2, respectively. The resultant matrix will be a 2×2 matrix. 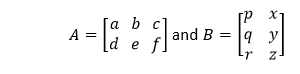
To find the first element of the resultant matrix, multiply the first row of matrix A by the first column of matrix B and sum up the product. (a,b,c).(p,q,r)=a×p+b×q+c×r To find the second element of the resultant matrix, multiply the first row of matrix A by the second column of matrix B and sum up the product. (a,b,c).(x,y,z)=a×x+b×y+c×z To find the third element of the resultant matrix, multiply the second row of matrix A by the first column of matrix B and sum up the product. (d,e,f).(p,q,r)=d×p+e×q+f×r To find the fourth element of the resultant matrix, multiply the second row of matrix A by the second column of matrix B and sum up the product. (d,e,f).(x,y,z)=d×x+e×y+f×z The resultant matrix is: 
Multiplication of a 2×2 matrix and 2×1 matrix
Multiplication of the two 2×2 matrix
Multiplication of 3×3 matrix
Similarly, we can find the multiplication of the matrices with different dimensions. Properties of Multiplication
Example 1: Multiply the following matrices. 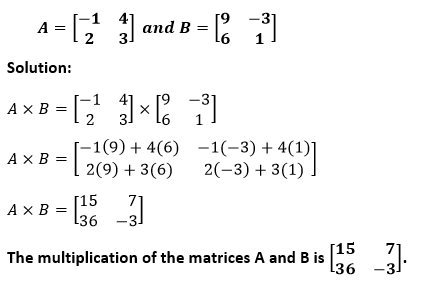


Example 4: 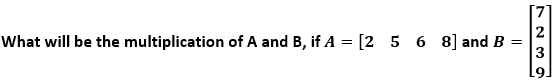
Solution: The dimensions of the matrix A and B are 1×4 and 4×1, respectively, so the resultant matrix will be of dimension 1×1. 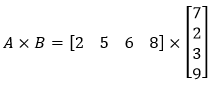
A×B=[2×7+5×2+6×3+8×9] A×B=[114] The multiplication of the matrices A and B is [114]. 
Solution: The dimensions of the matrix A and B are 3×2 and 2×1, respectively, so the resultant matrix will be of dimension 3×1. 
Solution: We know that the identity matrix is the matrix whose principal diagonal elements are 1 and other elements are zero is called an identity matrix. 
Example 8: Multiply matrix A by its negative matrix. 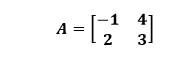
Solution: We have to find A×(-A) or -A2. The negative matrix of the matrix A is -A. It means to multiply each element of matrix A by the negative sign. 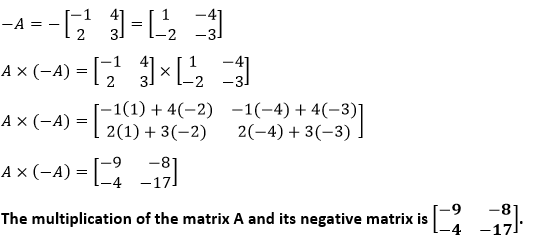
Next TopicEquivalent Fractions
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










