Matrix Multiplication in Discrete mathematics

Matrix

In discrete mathematics, we can deal with a lot of concepts with the help of matrices. A matrix is used to contain the rectangular array of numbers, and all these numbers, expressions, or symbols will be arranged in the form of rows and columns. There are several operations that can be performed on matrices, like subtraction, multiplication, addition, etc. In this section, we are going to learn about how to multiply two matrices, its formula, algorithms, examples of matrix multiplication, and many more.

Matrix multiplication

A French mathematician Jacques Philippe Marie Binet was introduced the concept of matrix multiplication in 1812. In discrete mathematics, matrix multiplication can be described as an operation that is performed in matrices. Suppose we have two matrices, A and B. We can multiply these matrices if and only if both the matrices are compatible. Multiplication of a matrix can also be described as a binary operation that provides us a matrix with the help of multiplication of two given matrices. In the below section, we will learn about the rules of matrix multiplication.

What is matrix Multiplication

The matrix multiplication is known as a binary operation which generates a matrix as an output when we multiply two matrices. If the given matrices are compatible, only then we will be able to multiply the matrices. Just like the arithmetic multiplication, the matrix multiplication will not be commutative, which indicates that the multiplication of matrices A and B provides us AB, which cannot be equal to BA in case of matrix multiplication, i.e., AB ≠ BA.

If there are two matrices, A and B, and the number of columns in matrix A and the number of rows in matrix B are similar to each other, then these matrices will be known as compatible. That means the matrices A and B will be compatible if matrix A contains an order m∗n and matrix B contains an order n∗p.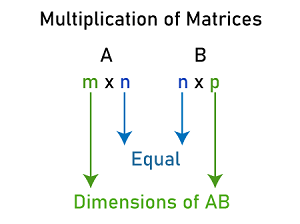

Suppose we have two matrices, A and B. When we multiply them, then we will get AB in the result. If there is a matrix A, which is an m∗n matrix, and another matrix B which is an n∗p matrix, then the multiplication of these matrices will be matrix C which is in the order m∗p.

Definition of Matrix multiplication

We can also call matrix multiplication as a matrix product. If there are two matrices and we multiply them, then the resultant matrix will be a single matrix. Matrix multiplication is a type of binary operation.

Suppose there are two matrices, A and B, then we can use the following way to indicate the product of these two matrices A and B:

X = AB

The product of two matrices is also known as the dot product of two matrices.

Matrix multiplication by Scalar

Scalar multiplication can be defined as a multiplication of an integer with a matrix. We know that a matrix can be described as an array of numbers. It is used to have rows and columns. If we have a matrix and we multiply it by a scalar value, then that multiplication will be known as scalar multiplication. There can be one more case where we can multiply the two matrices. We will understand the process of doing this with the help of an example.

In the following way, we can define the multiplication of a matrix by a scalar:

Suppose there is a matrix A = [a_ij]_m∗n and k is a scalar. If we multiply each element of A by scalar k, then we will get the result matrix kA. We can define it in one more way, i.e., kA = k [a_ij]_m∗n = [k(a_ij)]_m∗n, which indicates that (i, j)th element of kA is ka_ij for all possible values of i and j.

For example: In this example, we will multiply the matrix by scalar value 4. The matrix is shown below: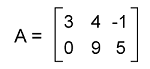

Solution: From the question, we have the following matrix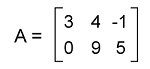

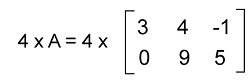
Now we will get the following matrix by multiplying each element of A by 4 like this: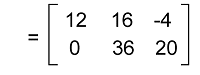

So we get this matrix after multiplying the given matrix by the scalar value 4.

Matrix multiplication condition

We can perform the multiplication operation of two given matrices only if the number of columns in 1^st matrix and the number of rows in 2^nd matrix are similar to each other. Therefore, the number of rows of 1^st matrix and the number of columns of 2^nd matrix will be contained in the result of matrix multiplication. So the order of resulting matrix will be known as the matrix multiplication order.

Notation

If there is a matrix A, which is an a∗b matrix, and another matrix B which is a b∗c matrix, then the multiplication of A and B can be described as follows:

X = AB

Here matrix X is used to indicate the resultant matrix, which has an m∗n dimension.

Formula of Matrix multiplication

We will use an example to understand the matrix multiplication formula, which is described as follows:

Suppose there are two matrices, A and B, in such a way that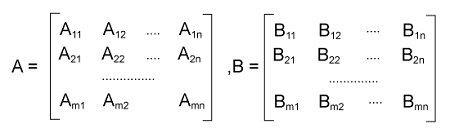

The resultant matrix C = AB can be indicated in the following way: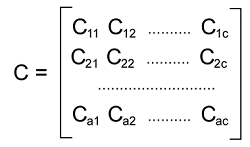

Here C is the resultant matrix which is get by multiplication of matrix A∗B. Suppose C has two elements, x and y. Then

C_xy = A_x1B_y1 + A_x2B_y2 + .... + A_xbB_by = ?^b_k=1 A_xkB_ky

For x = 1....a and y = 1....c

How to Multiply matrices

With the help of a technique, we can learn the process of multiplication of matrices, i.e., the first rows will be multiplied by each and every element of columns, and after that, the rows will be filled up. With the help of following steps, we will learn how we can perform matrix multiplication:

Step 1: In this step, we will check the matrices' compatibility by ensuring that the number of columns in the 1^st matrix and the number of rows in the 2^nd rows are similar to each other.

Step 2: In this step, we will multiply the element of 1^th row of 1^st matrix by the elements of j^th column in the 2^nd matrix. After that, we will add the products.

Step 3: In the last step, we will place all the added products in their respective positions.

Suppose we have two matrices, A and B, where A is an a∗b matrix and B is a b∗c matrix. The multiplication of both matrices will be indicated by matrix C in the following way:

C = AB

Suppose matrix C contains elements x and y. It will be defined as:

C_xy = A_x1B_y1 + A_x2B_y2 + .... + A_xbB_by = ?^b_k=1 A_xkB_ky

For x = 1....a and y = 1....c

Now we will use the following example to understand the above steps for multiplication of matrices.

Example: In this example, we will determine the multiplication of following matrices.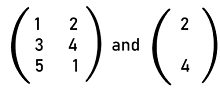

Solution: As we can see that the above matrices are of order 3∗2 and 2∗1. So these matrices are compatible because the number of columns of 1^st matrix and the number of rows of 2^st is similar. Now we can perform the multiplication on these matrices, and the resultant matrix will contain the order 3∗1.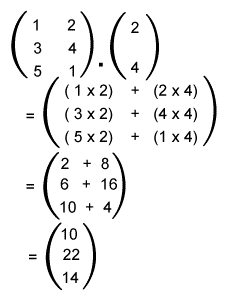

Hence the result of this multiplication is described as follows: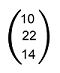

In the above output matrix, we can see that when we multiply the element of 1^st row of 1^st matrix by the corresponding element of 1^st column of 2^st matrix, and then after adding them, we will get the first element of first row. So we should use the following steps to determine the element of i^th row and j^th column in the multiplication matrix like this:

• First, we will choose the elements of i^th row of 1^st matrix.
• After that, we will choose the elements of j^th column of 2^nd matrix.
• Now, we will multiply the corresponding elements.
• Lastly, we will add the sum of all the products.

Algorithm of Matrix multiplication

In case of matrix multiplication, we have four types of algorithms, which are described as follows:

1. Sub-cubic algorithm
2. Divide and conquer algorithm
3. Parallel and distributed algorithm
4. Iterative algorithm

These algorithms are mostly used in a lot of programming languages, like Java, C, etc, to perform online multiplications. There are some most common matrix multiplications, i.e., 2∗2, 3∗3, 4∗4, etc. The operations of multiplication, subtraction, and addition will be performed on a matrix in the same way as we perform them on real or rational numbers.

Matrix multiplication is a type of operation which is used in linear algebra. The matrices are used to contain a lot of applications. With the help of matrix multiplication, we can show linear mapping, which includes scalar addition and multiplication.

On meshes, we can also determine a wide range of algorithms. With the help of this type of algorithm, we can minimize the inherent inefficiency of the standard array algorithm. In this case, there can be a delay in the arrival of data from two different matrices.

Rules of Matrix multiplication

As we know that if two matrices are compatible, only then we will be able to multiply those matrices. That means the number of columns in the first matrix and the number of rows in the seconds must be similar to each other for the multiplication of matrices. If there is a matrix A which is an m∗n matrix, and another matrix B which is an n∗p matrix, then the order of multiplication of these matrices will m∗p.

The rules and properties of matrix multiplication can be written in the following way with the help of above defined formula and procedure:

• We can define the multiplication of two matrices, A and B if the number of columns in A and the number of rows in B are similar to each other.
• If we define the AB, then we will not require defining BA.
• If we have defined both AB and BA, it will not require AB = BA.
• If we get a zero matrix as the result of multiplication of two matrices, then it will not be required that one of the matrices is a zero matrix.
• If there are two square matrices, A and B, which have the same number of orders, then both AB and BA are defined.

For example:

1. If we try to multiply a 4∗3 matrix by a 3∗4 matrix, then that matrix will be a valid matrix, which provides us a matrix of order 4∗4.
2. If there are two compatible matrices, 7∗1 and 1∗2, then the multiplication of these matrices will be a 7∗1 matrix.
3. There is no possibility of doing the multiplication of a 4∗3 matrix and a 2∗3 matrix.

2∗2 matrix multiplication

The process of doing the 2∗2 matrix and the process of doing matrix multiplication of any order will be the same. To do this multiplication, we will first use the first matrix and multiply each element of each row of this matrix by the elements of each column in the second matrix. Lastly, we will do the addition of these products. The multiplication of two 2∗2 matrices will generate the result in the form of a 2∗2 matrix.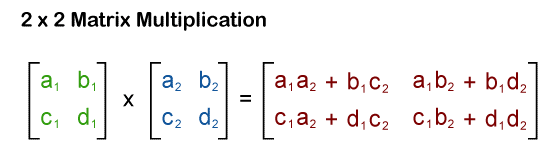

Suppose there are two 2∗2 matrices, A and B, and we will do the multiplication of these matrices in the following way. The A and B matrices are described as follows: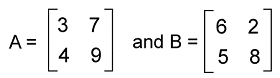

Now we will calculate each element of the product matrix AB in the following way:

AB₁₁ = 3∗6 + 7∗5 = 53

AB₁₂ = 3∗2 + 7∗8 = 62

AB₂₁ = 4∗6 + 9∗5 = 69

AB₂₂ = 4∗2 + 9∗8 = 80

Hence, the multiplication matrix is described as follows: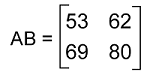

3∗3 Matrix Multiplication

With the help of matrix multiplication formula, we can perform the 3∗3 matrix multiplication. This is because any two 3∗3 matrices are compatible. The process of doing the 3∗3 matrix and the process of doing matrix multiplication of any order will be the same. The multiplication of two 3∗3 matrices will generate the result in the form of a 3∗3 matrix.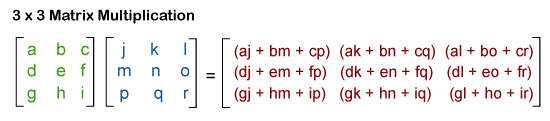

In this matrix, we can see that the matrices contain the same dimension. That's why the resultant matrix will also contain the same dimension 3∗3.

For example: Suppose there are two 3∗3 matrices, A and B, and we will do the multiplication of these matrices in the following way. The A and B matrices are described as follows: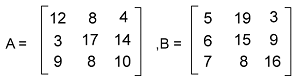

Now we will calculate each element of the product matrix AB in the following way:

AB₁₁ = 12×5 + 8×6 + 4×7 = 136

AB₁₂= 12×19 + 8×15 + 4×8 = 380

AB₁₃= 12×3 + 8×9 + 4×16 = 172

AB₂₁= 3×5 + 17×6 + 14×7 = 215

AB₂₂= 3×19 + 17×15 + 14×8 = 424

AB₂₃= 3×3 + 17×9 + 14×16 = 386

AB₃₁= 9×5 + 8×6 + 10×7 = 163

AB₃₂= 9×19 + 8×15 + 10×8 = 371

AB₃₃ = 9×3 + 8×9 + 10×16 = 259

Hence, the multiplication matrix is described as follows:

Properties of Matrix multiplication

There are some properties contained by the matrix multiplication, which are described as follows:

Commutative Property

The matrix multiplication does not contain the commutative property. The commutative law contains the following relation in the matrix multiplication:

AB ≠ BA

If we are doing the multiplication of two matrices, then the order will matter a lot. Now we will prove this with the help of an example which is described as follows:

For example:

Suppose there are two matrices, A and B where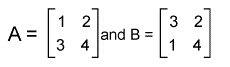

Then the multiplication of A∗B is described as follows: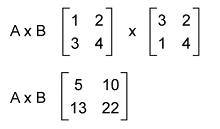

But, the multiplication of B∗A is described as follows: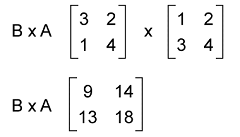

We can see that the matrix AB ≠ BA

Hence, the multiplication of two matrices cannot have the commutative property.

Associative Property

Suppose there are three matrices, A, B, and C. The associative law contains the following relation in the matrix multiplication:

(AB)C = A(BC)

Now we will prove this with the help of an example which is described as follows:

Suppose there are three matrices, A, B, and C where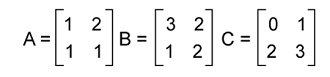

Now we will first solve the LHS(left-hand side) part of the equation, i.e., (AB)C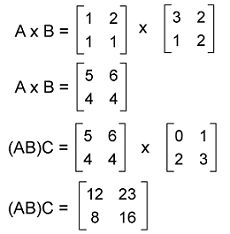

Now we will first solve the RHS(right-hand side) part of the equation, i.e., A(BC)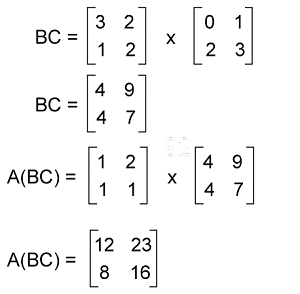

We can see that the LHS is equal to the RHS.

Hence, the multiplication of three matrices will have the associative property.

Distributive Property

According to the distributive law, if there are two numbers that are added together and if we multiply them by a number, then the result of this multiplication and the result of doing each multiplication of the matrices separately will be the same. Suppose there are three matrices, A, B, and C. The distributive law contains the following relation in the matrix multiplication:

A(B+C) = AB + AC

Multiplicative identity property

The identity law contains the following relation in the matrix multiplication:

I = I.A = A

Here, A is used to indicate the n∗n matrix, and I is used to indicate an identity matrix of order n.

Suppose there is a matrix A and an identity matrix I, which contains the following values: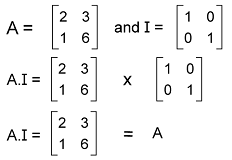

Dimension Property

In case of matrix multiplication, if there are two matrices m∗n and m∗a, then the product of these matrices will be m∗a matrix.

For example: If there is a matrix A which is a 2∗3 matrix, and another matrix B, which is a 3∗4 matrix, then the multiplication of these matrices AB will be 2∗4 matrices.

Transpose property

Suppose there are two matrices, A and B. We can get the transpose of a product of these two matrices with the help of doing the multiplication of transpose of individual matrices in reverse order. The symbol T is used to indicate the transpose. The transpose of A and B is described as follows:

(A∗B)^T = B^T ∗ A^T

Complex Conjugate

If there are two complex entries, A and B, in this case, (AB)^∗ = B^∗A^∗.

Product with scalar

If there are two matrices, A and B, then the product of these matrices with the scalar value c will be distributed as follows:

c(AB) = (cA)B = A(Bc)

Multiplication Property of Zero

Suppose there is a zero matrix, and if we multiply it by a given matrix, then we get the zero matrix as a resultant matrix.

Suppose there is a zero matrix and a matrix A where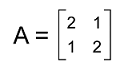

The product of matrix A and zero matrices is described as follows: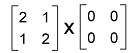

The resulting matrix will be a zero matrix, which is described as follows: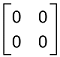

Important Points

There are some important points that we should know while learning matrix multiplications. These points are described as follows:

• If we want to multiply the matrices, then these matrices must be compatible.
• With the help of following rule, we can get the order of a product matrix:
  If there is a matrix A which is an m∗n matrix, and another matrix B which is an n∗p matrix, then the order of multiplication of these matrices will m∗p.
• With the help of row-by-column multiplication, we can indicate the multiplication of matrices.

Example of Matrix multiplication

Matrix multiplication is used to contain a lot of examples, and some of them are described as follows:

Example 1: In this example, we will use the formula of matrix multiplication and determine the multiplication of matrices AB where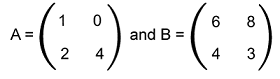

Solution: As we can see that the above matrices are of order 2∗2. So these matrices are compatible because of the same order. Now we can perform the multiplication on these matrices, and the resultant matrix will contain the order 2∗2.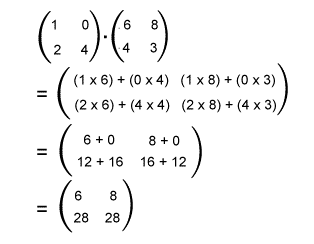

Hence the multiplication of these matrices is described as follows:

Example 2: In this example, we will use the previous example (example 1) and determine the BA. After this, we will check if AB = BA? Lastly, we will check whether the statement "matrix multiplication is commutative" is true or not.

Solution: First, we will do the multiplication of BA in the following way:

From example 1 and example 2, we can see that AB ≠ BA.

As we know that value of BA is:

And AB ≠ BA, so the matrix multiplication is not commutative.

Example 3: In this example, we will assume that there are two 4∗4 matrices, A and B, and we have to multiply them. The value of matrices A and B are shown below:

Solution: After multiplying both the matrices with the help of using same steps as described above, we will get the following matrix as a resultant matrix:

Example 4: In this example, there are two matrices, A and B, where A is used to contain the order 4∗1, and B is used to contain the order 1∗3. We have to check whether we can define both products AB and BA.

Solution: From the question, we know that

Matrix A is used to contain the order 4∗1

Matrix B is used to contain the order 1∗3.

We can do the multiplication of AB only when the number of column in A and the number of rows in B is similar to each other. With the help of rules of matrix multiplication, we will get the resultant matrix as an order 4∗3. We cannot define the multiplication of BA. This is because the number of columns in B and the number of rows in A are not similar to each other. Now we know that one of the multiplications cannot be defined, and the multiplication of AB is not necessarily equal to the multiplication of BA. Hence the matrix multiplication is not commutative.

Hence the product AB can be defined, but the product of BA cannot be defined.