Minimum Number of Flips to Convert Binary Matrix into Zero Matrix in Java

It is a very interesting problem frequently asked in interviews of top IT companies like Google, Amazon, TCS, Accenture, etc. By solving the problem, one wants to check the logical ability, critical thinking, and problem-solving skill of the interviewee. So, in this section, we are going to solve the minimum number of flips to convert the binary matrix into a zero-matrix problem in Java with different approaches and logic. Also, we will create Java programs for the same.

Binary Matrix

A boolean matrix is a matrix whose all elements are either 1 or 0.

Zero Matrix

A zero matrix is a matrix whose all elements are zero. Therefore, a zero matrix contains only zero's as its elements are called a zero or null matrix. Note that a zero matrix can be a square matrix. It is denoted by the letter O. For example, consider the following matrix:

Problem Statement

We have given a binary matrix of m*n. At a time, we can choose one cell and flip its and all the four neighbors of the matrix if they exist (flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighbors if they share one edge.

The task is to return the minimum number of flips required to translate the binary matrix to a zero matrix, else return -1.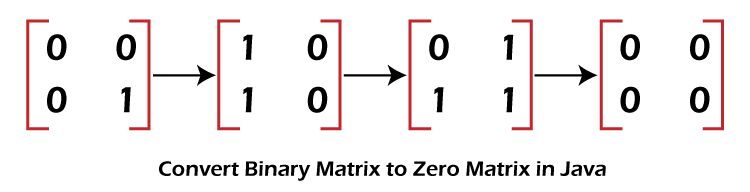

The above matrix can be converted into a zero matrix in three flips that are (1, 0), (0, 1), and finally (1, 1) as shown above.

Let's see some other examples.

Example 1:

Input: matrix = [[1,0,0], [1,0,0]]

Output: -1

Explanation: The given matrix cannot be converted to a zero matrix.

Example 2:

Input: matrix = [[1,1,1], [1,0,1], [0,0,0]]

Output: 6

Explanation: The given matrix required six flips to convert into a zero matrix.

Solution to The Problem

The problem can be solved by using the following two approaches:

1. DFS, Backtracking, and Memorization
2. BFS, Memorization, and Bit Operation

Using DFS, Backtracking, and Memorization

In this approach, for each cell either we flip at all or we flip it once. Note that any cell cannot flip more than one. It ensures 2^(m*n) possible states, where m and n are at most 3. Therefore, we can check each possible state which is reachable from the initial state. It gives the minimum cost of transit from the initial state to the final state which is 0.

Let's understand it through an example.

Consider an array say arr. It avoids the same state more than once. Suppose, arr[i] is the minimum lips required to transit from state i to 0.

If a flip (from i1 to i2) has been transit before, it means we just entered into a cycle. In this cycle, some flips may be wasted and may be made no state transition progress. In order to overcome the problem, we need a boolean array to track the state if we have visited before. If we have visited the state before, return -1 to indicate the flips belongs to a cycle and is not going to yield a possible result.

Algorithm

1. Initialize dp and seen array, dp[0] = 0;
2. Begin from the initial state, try each different cell to flip. Now recursively solve (steps i, ii, and iii) all the next states that give the minimum cost among all possible states.
   1. If we have visited the state before, return -1. It indicates that the previous flip picks are not going to be an answer;
   2. Else compute a state that has a valid result to it. Return the result without re-computing the state.
   3. Otherwise, we need to compute the state using backtracking. Mark the state as visited. After that, for each possible next state, do a flip that leads to the next state.
   4. Recursively solve for this next state, then flip the same cell back to finish the backtracking. After solving all the possible next states and updating the current state's result, mark the current state as unvisited to finish the backtracking.

Let's implement the above algorithm in a Java program.

NumberOfFlip.java

Output:

The minimum number of flips required is: 6

Complexity

The time and space complexity is O(2^{(m * n)}) because we check each state once.

BFS, Memorization, and Bit Operation

The problem can also be solved by using the BFS. In this approach, we treat a flip from state S1 to S2 (as we have done in the previous approach) in one step and keep track of each state's result. When we first time update one state's result, the BFS ensures the bare minimum cost when going from the initial state. In such a case, we add new states to the BFS queue. Later, if we get a bigger cost for the same state, ignore it. The approach ensures each possible state compute only once.

Algorithm

1. To get the initial state, use bit operation.
2. Initially all states to be Integer.MAX_VALUE and the state cost is 0.
3. Add initial state to the queue and perform BFS as follows:
   1. If reaching state is 0, return its bare minimum cost;
   2. Else, try all the possible flips at different cells by using the XOR operations.
   3. If the next state is computed for the first time, add it to the queue.
4. Return -1 if all states are exhausted without success.

Let's understand it through an example.

Min steps => BFS

Key: Compress the matrix to an integer/ bit set.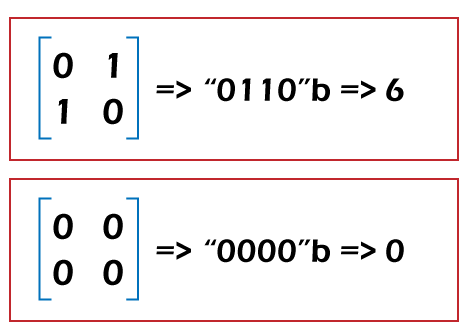

Note: Flip the i-th bit of an integer i.e. x^=(1 << i).

Let's implement the steps in an algorithm.

Algorithm

Let's implement the above steps in a Java program.

Java Program to Convert Binary Matrix into Zero Matrix

NumberOfFlips.java

Output:

The minimum number of flips required is: 3

Complexity

The time and space complexity is O(2^{(m * n)}). Note that the approach is faster than the previous one.