Multiple Regressions of SPSSIn this section, we are going to learn about Multiple Regression. Multiple Regression is a regression analysis method in which we see the effect of multiple independent variables on one dependent variable. For this, we will take the Employee data set. This data set is arranged according to their ID, gender, education, job category, salary, salary at the beginning, job time, previous experience, and whether they belong to a minority community or not. 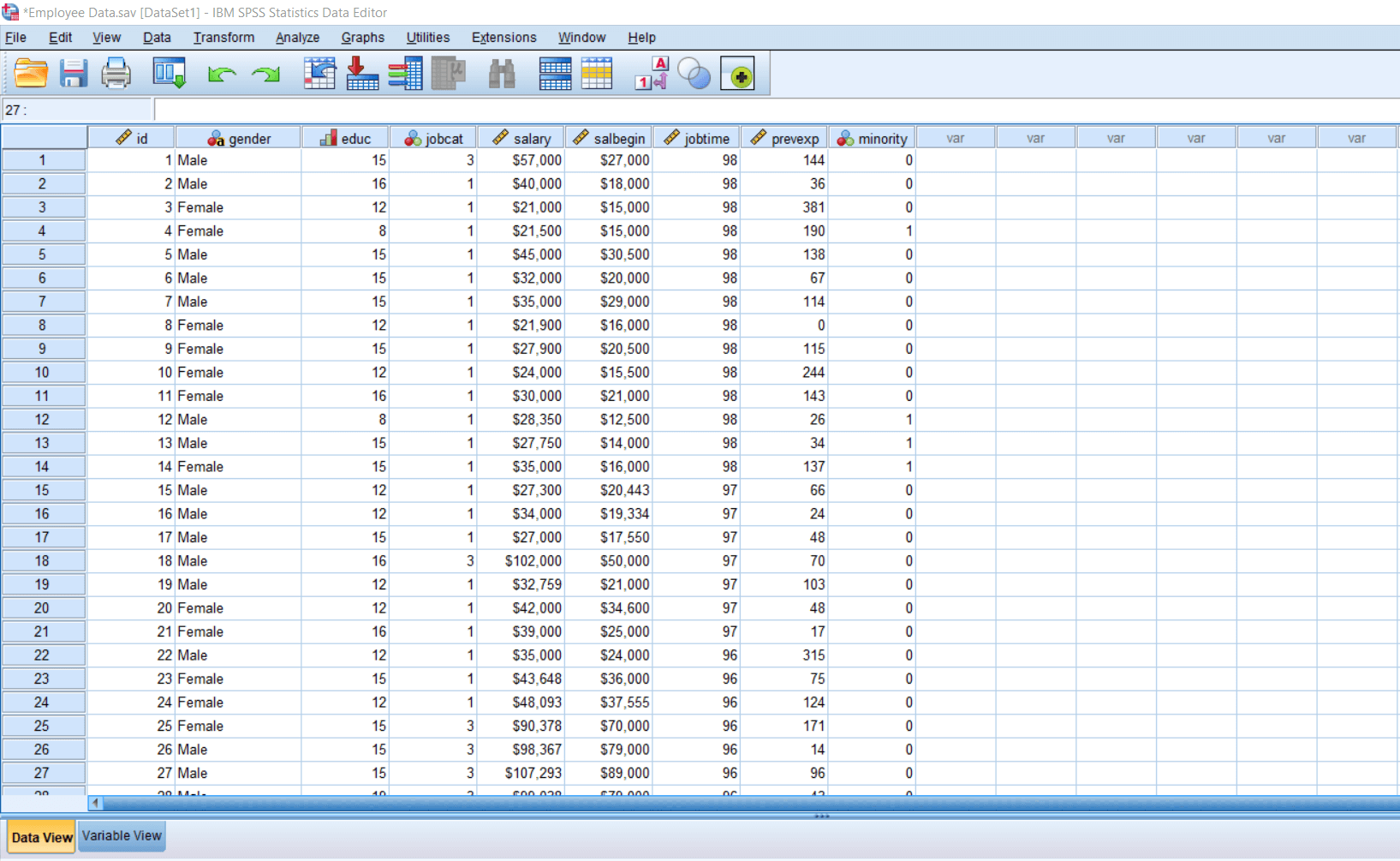
Now suppose in this data set, we want to find out what exactly determines the Current Salary drawn by the employees. 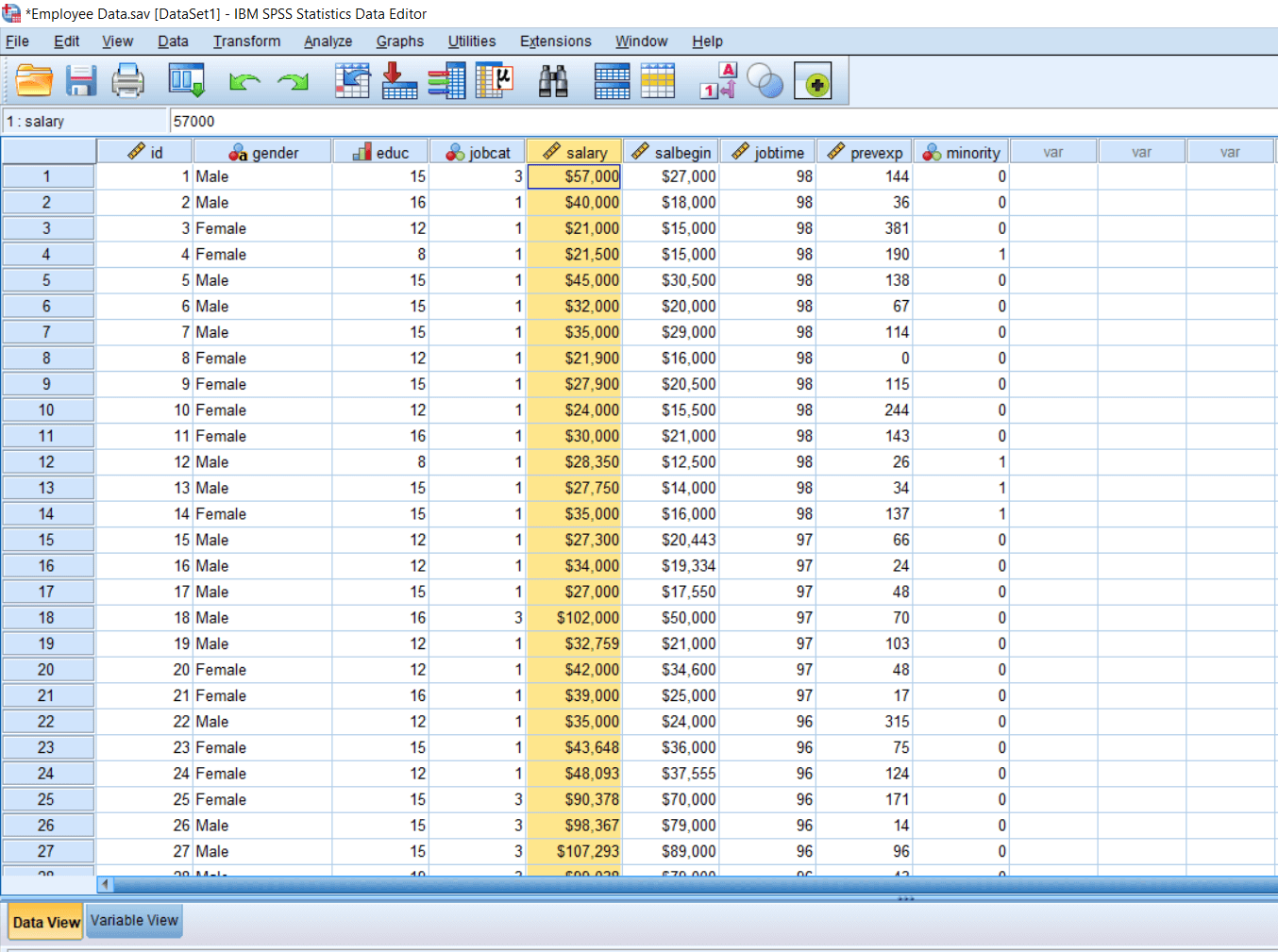
The current salary can be determined by their salary at the time of joining because it's logical to assume that those employees who are drawing a higher salary at the time of joining they will also draw a higher salary currently. We can also guess that the employee's experience will also contribute to the salary they are drawing. Apart from this, we also have an education. So education is again an important criterion for determining the salary. Those highly educated employees can presume that they are drawing a higher amount of salary compared to those who are less educated. 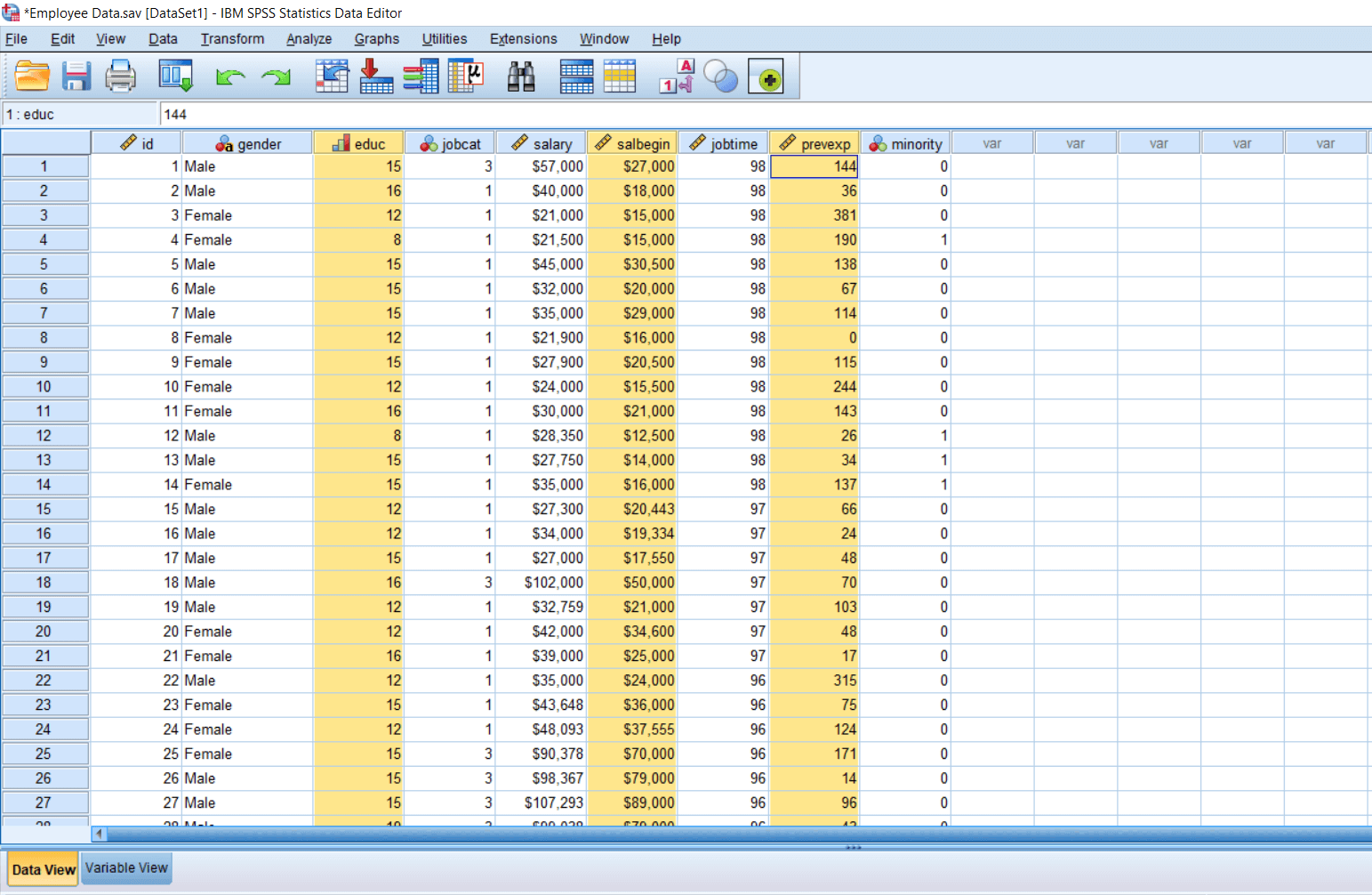
Similarly, we can also guess that salary drawn will also be affected by the employee's position. In our case, we have three categories of employees, i.e., Clerical, Custodial, Manager. 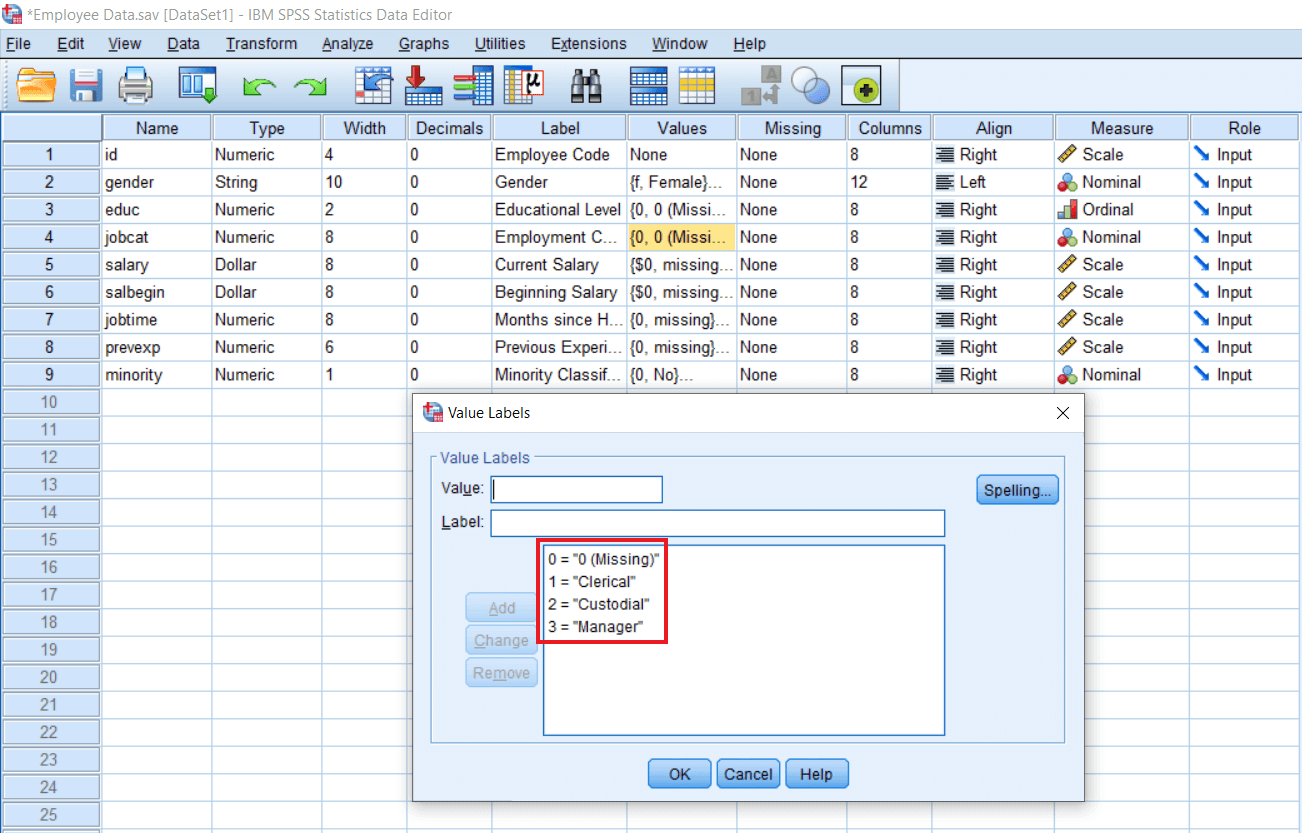
We will guess that Managers are drawing a higher salary as compared to Clerical or Custodial employees. Suppose we want to test these assumptions that job category, education, or position of the employee or the salary at the time of joining the organization are the influence factors in the employee's current salary. In that case, we have to run the multiple regression analysis. The idea of multiple regression analysis is very clear. When we want to predict one dependent variable in our case, it's a Current salary by many independent variables like education, job category, beginning salary, job timing, previous experience, then we can perform a multiple regression analysis. When we perform a multiple regression analysis, our variables must be logically selected. For example, do we believe that being in a minority status does affect the salary of a person. Well, it may or may not. So, it's interesting to say this, but theoretically, if we find any justification that minority affiliation of the person may affect his or her salary, then we can include that variable as well in the multiple regression analysis, or if we want to include all the variables in our multiple regression analysis, we can do that. SPSS is going to tell whether this variable exercises a significant influence on the dependent variable or not. 
The model of Multiple Regression is very simple. We have to select a dependent variable. Generally, we denote our dependent variable by the symbol y, and then we have many independent variables, and we can call them x1, x2, x3 till we can have xn. (y = x1 x2 x3 + ----- + xn Now we are going to get the coefficient by applying the multiple regression analysis. So suppose those constant or coefficient is α1x1 + α2x2 + α3x3 till αnxn. Now we will make a prediction. Now we are predicting y based on these x variables from x1 till xn. We will make some error because we cannot always find all those variables that will completely predict y. So these are bound to some error term. Again, we are going to find that out. Apart from that, we are going to have a constant as well in our regression equation. y = α1x1 + α2x2 + α3x3 + ----- + αnxn + error + constant So that's our typical theoretical regression model. Now we have to use the word α, but most typically, people use the word β, so we can again rewrite the equation as β1x1 + β2x2 + β3x3 till we have βnxn then our error term plus constant term. y = β1x1 + β2x2 + β3x3 + ----- + βnxn + error + constant This β is the standardized regression weights that we are going to get after the regression analysis. In our case, we wanted to predict the Current Salary of the employee. So, we will write our multiple regression equation as Current Salary = β1. Now take one variable as the employee's beginning salary, so Current Salary = β1* Beginning salary. Current Salary = β1* Beginning salary Now we can take our second variable as education. So for that, we are going to get a second coefficient that is β2* education category. Current Salary = β1* Beginning salary + β2* education category Then the third variable we may take as an experience. So for that, we are going to get a third coefficient that is β3* experience. So we have built a sample model by taking into three variables. Current Salary = β1* Beginning salary + β2* education category + β3* experience If we want to take more variables, we can do that. We can make a lengthy or complex regression model. Now we are going to add our error term and then constant. So that makes our regression model clear. Current Salary = β1* Beginning salary + β2* education category + β3* experience + error + constant We can see, in the case of multiple regression analysis, we can take our independent variable as either a nominal variable or a metric variable. The independent variable could be metric or non-metric. But our dependent variable in case of multiple regression analysis or linear regression analysis or hierarchy regression analysis should always be metric. Current Salary = β1* Beginning salary + β2* education category + β3* experience + error + constant
Next TopicEnter method of Multiple Regression
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










