Order of Group in Discrete Mathematics

The term order can be specified into two closely related senses in the group theory:

• The group"s order can be described by its cardinality, which means the number of its elements.
• Sometimes, an order can be called a period. So in a group, the order of element 'a" is the positive integer 'm". The relation between a and m is described as follows:

Where

a^m is used to specify the product of m copies of a

e is used to specify the identity element of a group

If the order of a group does not have m, a will be known to have the infinite order. In the finite group, all elements will have finite order.

|G| or ord(G) is used to specify the order of group G.

|a| or ord(a) is used to specify the order of an element a.

Example: In this example, we will describe the multiplication table of the symmetric group S₃.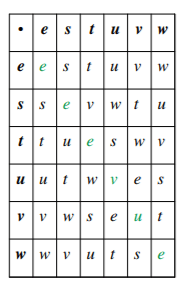

There are 6 elements in the above group. So ord(S₃) = 6. When we execute the above table, the identity"s order e is 1. Each of s, t, and w squares to e, which means the group elements s, t, and w have order 2. When the enumeration will complete, u and v both will have the order 3 for u² = v, u³ = vu = e, and v² = u and v³ = uv = e.

Order and Structure

The structure of a group can be described using the order of a group and an element. In other words, the group will be complicated if the factorization of the order is complicated.

The group will be known as the trivial group if the order of a group is 1. Suppose we have an element x, then x will be called identity only if the ord(x) = 1. The order of group ord(x) will be 2 if every element of x group is equal to its inverse, and consequently, group G will be abelian. Since xy = (yy)xy(xx) = y(yx)(yx)x = yx. If we are trying to converse this statement, it will not be true. For example, if the cyclic group Z₆ contains 6 integer modules, this group will be abelian, but number 2 contains the order 3 (2+2+2 = 6 = 0 (mod6)).

The two concepts of order have some relationship, which is described as follows:

If a generates the subgroup, then

For any integer k, if we have ord(a) divides k, only then we will have the following relation:

In general, we can say that the order of G is divided by the order of subgroup of G. More precisely: if the group G has subgroup H, then they will have the following relation:

Where

[G : H] is used to show the index of H in G, an integer. This is known as Lagrange"s theorem.

The above relation will generate some immediate consequences in which the order of a group will be divided by the order of every group"s element. For example, in the above symmetric group, we have seen that the ord(S₃) = 6 and the element"s order are 1, 2, or 3.

For the finite group, the below partial converse will be true. If d is a prime number and it divides the group"s order G, there will be an element of order d in G. This is known as Cauchy"s theorem. For the composite orders, this statement is not true because the element of order four does not exist in the Klein four-group, which is described in the inductive proof. This theorem generates some consequences that say that if ord(a) is some power of p for every 'a" in G, only then the group"s order will be the power of prime p.

All power of a will be in finite order if 'a" has finite order. Now we will describe the formula for order of power 'a" if it has finite order:

Where

k describes an integer.

The order of inverse of a(a^-1) and a is equal to each other or the same.

We have no formula that can explain the order of a, b, and the order of product ab. There can be a case in which ab has infinite order, but a and b both have finite order. There can be another case in which ab has finite order, but a and b both have infinite order. If a and b has the relation ab = ba, it will be possible that ord(ab) divides lcm(ord(a), odr(b)). This statement generates consequences, which can prove that if m is used to specify the maximum of all order of group"s element in an abelian group, then every order of element divides m.

Counting by Order of Element

To explain counting by order of elements, we will assume that G is used to specify the finite group of order n and d is used to specify the divisor of n. The element"s number in G of order d is a multiplication of φ(d). Where φ is used to specifying the Euler"s totient function, which is used to provide the number of positive integers, but the value of integer will not be larger than d. For example, we have a case S₃ in which φ(3) = 2, and order 3 has exactly two elements. There is no useful information provided by this theorem about the elements of order 2, because φ(2) = 1. The composite d has only one limited utility, that is, d = 6 since φ(6)=2. It means that in S₃, order 6 has 0 elements.

In relation to homomorphisms

The order of elements can be reduced with the help of group homomorphisms. If homomorphisms are shown by relation f: G → H and 'a" is an element of G and has a finite order, then ord(a) will be divided by ord(f(a)). The ord(f(a)) will be equal to ord(a) or ord(f(a)) = ord(a) if f is injective. We can use this statement to prove that two concrete given groups have not contained homomorphisms(injective). For example, the relation h: S3 → Z5 has no nontrivial homomorphism because each and every number in Z5 except 0 contains the order 5. In S3, the number 0 can"t divide the order 1, 2, and 3 of elements. There are some further consequences of this through which conjugate elements will contain the same order.

Class Equation

The class equation can be described as the important result about orders. It is used to relate the finite group"s order G to its center"s order Z(G) and the size of its non-trivial conjugacy classes, which is described as follows:

Where

d_i is used to specify the size of non-trivial conjugacy classes. These can also be described as the proper divisor of |G|, which is more than 1. They are also the same as indices of centralizers in G. It is also used to represent the non-trivial conjugacy classes. For example, the trivial group can be indicated by the center of S₃, which contains only one element, 'e". The equation of S₃ is described as follows: