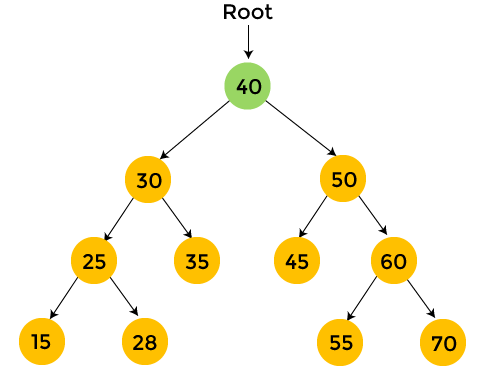
Preorder TraversalIn this article, we will discuss the preorder traversal in data structure. Linear data structures such as stack, array, queue, etc., only have one way to traverse the data. But in a hierarchical data structure such as tree, there are multiple ways to traverse the data. In preorder traversal, first, root node is visited, then left sub-tree and after that right sub-tree is visited. The process of preorder traversal can be represented as - Root node is always traversed first in preorder traversal, while it is the last item of postorder traversal. Preorder traversal is used to get the prefix expression of a tree. The steps to perform the preorder traversal are listed as follows -
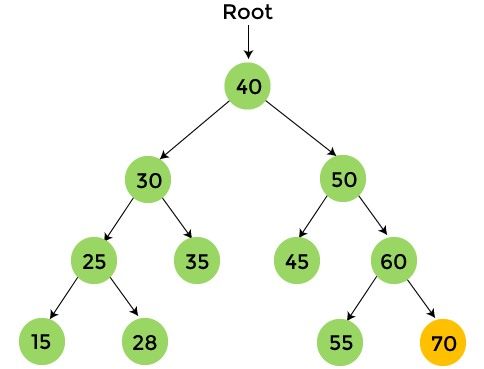
The preorder traversal technique follows the Root Left Right policy. The name preorder itself suggests that the root node would be traversed first. AlgorithmNow, let's see the algorithm of preorder traversal. Example of preorder traversalNow, let's see an example of preorder traversal. It will be easier to understand the process of preorder traversal using an example. 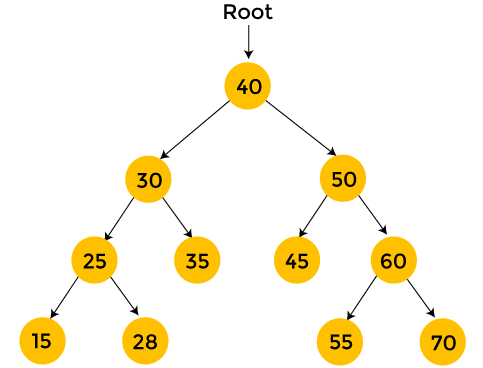
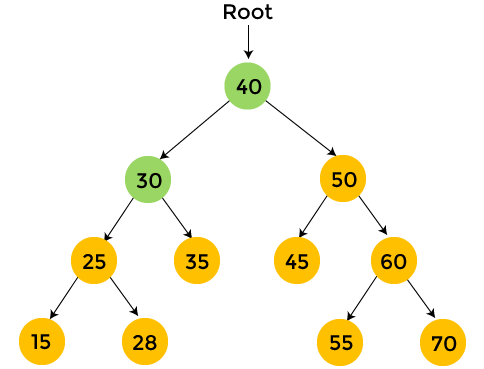
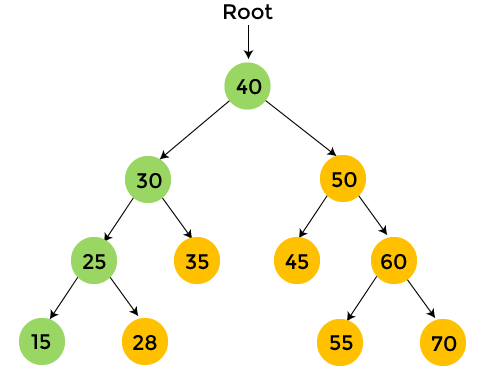
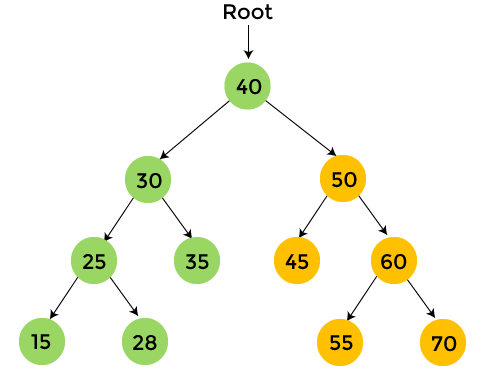
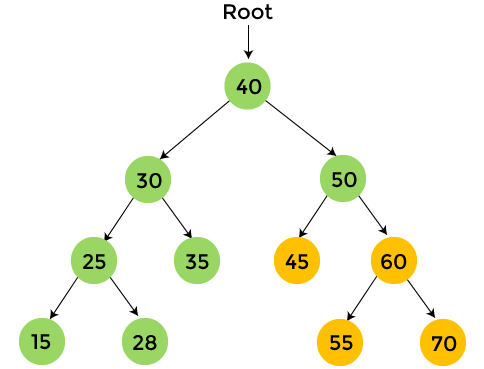
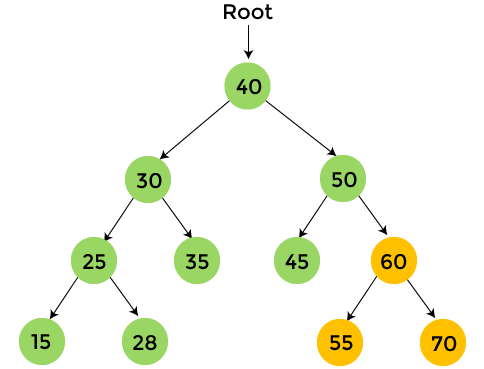
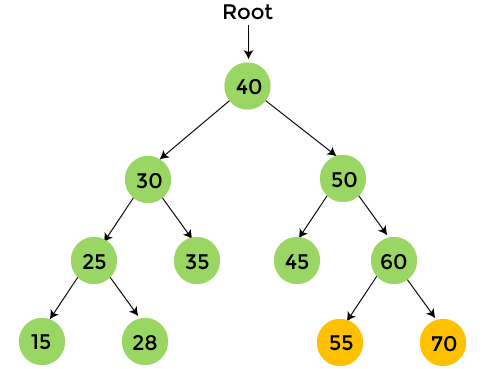
The nodes with yellow color are not visited yet. Now, we will traverse the nodes of the above tree using preorder traversal.
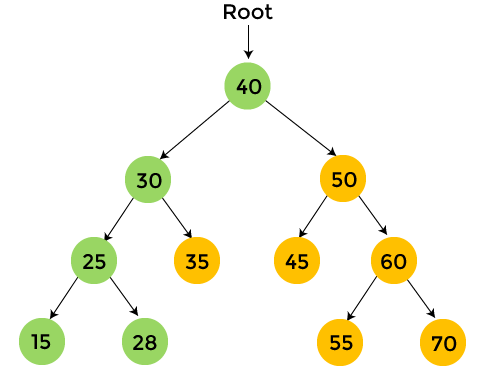
After the completion of preorder traversal, the final output is - 40, 30, 25, 15, 28, 35, 50, 45, 60, 55, 70 Complexity of Preorder traversalThe time complexity of preorder traversal is O(n), where 'n' is the size of binary tree. Whereas, the space complexity of preorder traversal is O(1), if we do not consider the stack size for function calls. Otherwise, the space complexity of preorder traversal is O(h), where 'h' is the height of the tree. Implementation of Preorder traversalNow, let's see the implementation of preorder traversal in different programming languages. Program: Write a program to implement preorder traversal in C language. Output After the execution of the above code, the output will be - 
Program: Write a program to implement preorder traversal in C++. Output After the execution of the above code, the output will be - 
Program: Write a program to implement preorder traversal in C#. Output After the execution of the above code, the output will be - 
Program: Write a program to implement preorder traversal in Java. Output After the execution of the above code, the output will be - 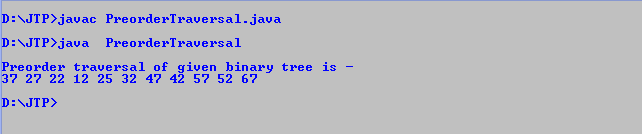
So, that's all about the article. Hope the article will be helpful and informative to you.
Next TopicTree Traversal
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share