Prism Formula

In Physics, a Prism is defined as a transparent, polished flat optical element that reflects light. These can be made from any transparent material with wavelengths that they are designed for. The most commonly used material is glass, fluorite, and plastic.

A polyhedron with two polygonal bases parallel to each other is a prism. In optics, the prism is the transparent optical element with flat polished surfaces that refract light. Lateral faces join the two polygonal bases, and these lateral faces are mostly rectangles. It may be a parallelogram in some cases. We can use the concept of prism in both mathematics and science as well.

Prisms called dispersive prism are used to break the light into its spectral colors. Other uses of prisms are to split light into its components with light polarization or reflect light.

In general, the Prism Formulas are given as,

Derivation of Prism Formula

OP is the incidence ray, making the angle i1 with normal, and QR is the angle of emergence, which i2 represents. A is the prism angle, and μ is the refractive index of the prism. Now, we know that,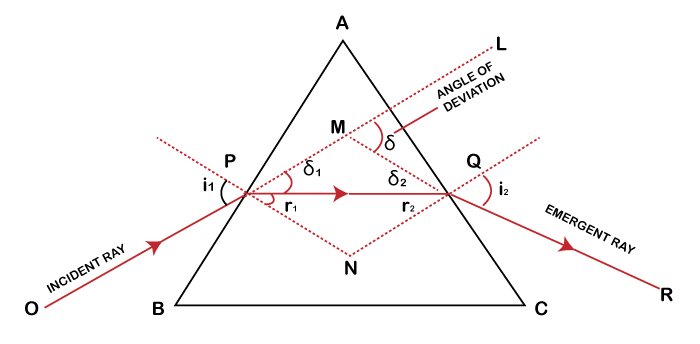

Properties of Prism

Here are some properties of the prism, such as:

1. The base and top are parallel and congruent.
2. Each face is a parallelogram except the base and top. These faces are called Lateral faces.
3. With every lateral face, one edge in common with the base and also with the top.
4. he height of the prism is the common edge of two adjacent side faces.

Types of Prism

Prisms are of different types. They are named based on the base shape of a prism. The types of prisms are rectangular prism, triangular prism, pentagonal prism, and hexagonal prism.

1. Rectangular Prism

A Prism that has 2 parallel rectangular bases and 4 rectangular faces is a Rectangular Prism. The Rectangular Prism Formulas are,

Where,

b - Base length of the rectangular prism

l - Base width of the rectangular prism

h - The height of the rectangular prism

2. Triangular Prism

A prism with 3 rectangular faces and 2 parallel triangular bases is a triangular prism.

Where,

a - Apothem length of the triangular prism

b - Base length of the triangular prism

h - The height of the triangular prism

3. Pentagonal Prism

A prism that has 5 rectangular faces and 2 parallel pentagonal bases is a pentagonal prism. The Pentagonal Prism Formulas are,

Where,

a - Apothem length of the pentagonal prism

b - Base length of the pentagonal prism

h - The height of the pentagonal prism

4. Hexagonal Prism

A hexagonal prism is a type of prism that has six rectangular faces and two parallel hexagonal bases. The Hexagonal Prism Formulas are,

Where,

a - Apothem length of the hexagonal prism

b - Base length of the hexagonal prism

h - The height of the hexagonal prism