Probabilistic reasoning in Artificial intelligence

Uncertainty:

Till now, we have learned knowledge representation using first-order logic and propositional logic with certainty, which means we were sure about the predicates. With this knowledge representation, we might write A→B, which means if A is true then B is true, but consider a situation where we are not sure about whether A is true or not then we cannot express this statement, this situation is called uncertainty.

So to represent uncertain knowledge, where we are not sure about the predicates, we need uncertain reasoning or probabilistic reasoning.

Causes of uncertainty:

Following are some leading causes of uncertainty to occur in the real world.

1. Information occurred from unreliable sources.
2. Experimental Errors
3. Equipment fault
4. Temperature variation
5. Climate change.

Probabilistic reasoning:

Probabilistic reasoning is a way of knowledge representation where we apply the concept of probability to indicate the uncertainty in knowledge. In probabilistic reasoning, we combine probability theory with logic to handle the uncertainty.

We use probability in probabilistic reasoning because it provides a way to handle the uncertainty that is the result of someone's laziness and ignorance.

In the real world, there are lots of scenarios, where the certainty of something is not confirmed, such as "It will rain today," "behavior of someone for some situations," "A match between two teams or two players." These are probable sentences for which we can assume that it will happen but not sure about it, so here we use probabilistic reasoning.

Need of probabilistic reasoning in AI:

• When there are unpredictable outcomes.
• When specifications or possibilities of predicates becomes too large to handle.
• When an unknown error occurs during an experiment.

In probabilistic reasoning, there are two ways to solve problems with uncertain knowledge:

• Bayes' rule
• Bayesian Statistics

Note: We will learn the above two rules in later chapters.

As probabilistic reasoning uses probability and related terms, so before understanding probabilistic reasoning, let's understand some common terms:

Probability: Probability can be defined as a chance that an uncertain event will occur. It is the numerical measure of the likelihood that an event will occur. The value of probability always remains between 0 and 1 that represent ideal uncertainties.

We can find the probability of an uncertain event by using the below formula.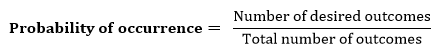

• P(¬A) = probability of a not happening event.
• P(¬A) + P(A) = 1.

Event: Each possible outcome of a variable is called an event.

Sample space: The collection of all possible events is called sample space.

Random variables: Random variables are used to represent the events and objects in the real world.

Prior probability: The prior probability of an event is probability computed before observing new information.

Posterior Probability: The probability that is calculated after all evidence or information has taken into account. It is a combination of prior probability and new information.

Conditional probability:

Conditional probability is a probability of occurring an event when another event has already happened.

Let's suppose, we want to calculate the event A when event B has already occurred, "the probability of A under the conditions of B", it can be written as: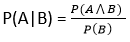

Where P(A⋀B)= Joint probability of a and B

P(B)= Marginal probability of B.

If the probability of A is given and we need to find the probability of B, then it will be given as: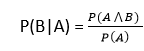

It can be explained by using the below Venn diagram, where B is occurred event, so sample space will be reduced to set B, and now we can only calculate event A when event B is already occurred by dividing the probability of P(A⋀B) by P( B ).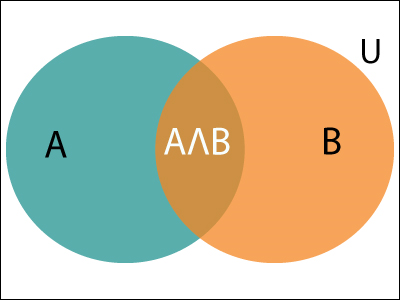

Example:

In a class, there are 70% of the students who like English and 40% of the students who likes English and mathematics, and then what is the percent of students those who like English also like mathematics?

Solution:

Let, A is an event that a student likes Mathematics

B is an event that a student likes English.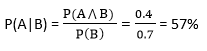

Hence, 57% are the students who like English also like Mathematics.