Proper Fraction Definition

What is a Fraction?

Generally, a fraction means a part of something. Mathematically, Fraction is a term used to represent a part of the whole. A Fraction has two parts: The dividend is called Numerator and the divisor is called Denominator. Numerator is an integer that represents the amount or number of parts selected. The denominator is an integer that represents the total number of parts.

For example: Suppose you are celebrating your birthday and want to serve a piece of cake to each of your six friends. You divide the cake into six equal parts and give one piece to each friend. So what Fraction of the cake your friends got? The answer is 1/6. Here, 1 is the numerator, and 6 is the denominator.

There are three types of fractions:

1. Proper Fraction,
2. Improper Fraction, and
3. Mixed Fraction

In this article, we are going to study proper fractions.

What is a Proper Fraction?

A proper fraction is a fraction whose numerator value is always less than the value of its denominator. Thus the value of a proper fraction will always be less than 1.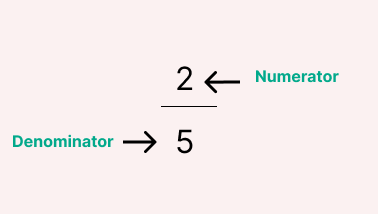

Let us take a square and divide it into four equal parts. Now let's study proper fractions through this example.

• If we take one part out of four parts, then the fraction becomes 1/4. Since the numerator is less than the denominator, the fraction is a proper fraction.
  
• Now let us take two parts out of four parts, and then the fraction becomes 2/4 or 1/2. Since here also, the numerator is less than the denominator here, this fraction is also a proper fraction.
  
• If we take three parts out of four, the fraction becomes 3/4, which is also a proper fraction.
  
• However, if we take four parts out of four, the fraction becomes 1, which is not a proper fraction, as a proper fraction is always less than 1.

Here are a few more examples of proper fractions:

Operations Performed on Proper Fraction:

Addition: When we have two proper fractions with the same denominators, the result is obtained by directly adding the numerators of both fractions, keeping the denominator the same.

For example, adding 1/6 and 3/6 is (1+3)/6 which equals 4/6 or 2/3.

When the two proper fractions have different denominators, then the equivalent fractions are formed by taking the LCM of the two denominators. Then the numerators of equivalent fractions are added.

For example: To add 2/3 and 1/4, we take the LCM of the denominators. Thus, the LCM of 3 & 4 is 12. We multiply the fraction with a number to make the denominator equal to its LCM. Here the numerator and denominator of 2/3 are multiplied by 4, equal to 8/12. And the numerator and denominator of 1/4 are multiplied by 3 to get 3/12. Now we add both numbers to get (8+3)/12 which is 11/12.

Subtraction: Subtraction of two proper fractions is also done in the same way as the addition. For example, the subtraction of 3/6 and 1/6 is (3-1)/6, equal to 2/6 or 1/3.

And the subtraction of 8/9 and 3/4 is (32-27)/36, which equals 5/36.

Multiplication: Multiplication of two proper fractions is done simply by multiplying the two numerators and denominators with each other. For example: Multiplication of 2/3 and 3/5 is (2x3)/(3x5) which is equal to 6/15 or 2/5.

Division: The division of two proper fractions is done by multiplying the first fraction with the reciprocal of the second fraction. For example, The division of 2/3 and 3/5 is 2/3 multiplied by 5/3, that is (2x5)/(3x3), which equals 10/9.

What is the difference between a Proper Fraction and an Improper Fraction?