QuantizationQuantization is a process to convert the continuous analog signal to the series of discrete values. A quantizer is a device known to perform the quantization process. The function of quantizer is to represent each level to the fixed discrete finite set of values. The signals during transmission over long distances suffer from noise and interference. To overcome this, the quantization process creates a signal that is approximately equal to the message signal. It selects a quantized signal mq(t) with values nearest to the original analog signal m(t). The quantization process selects a value and rounds off these values to the nearest stabilized value. The quantized signal mq(t) can get easily separable from the additive noise. Let's consider an example of the analog signal confined to the range VA to VB, as shown below: 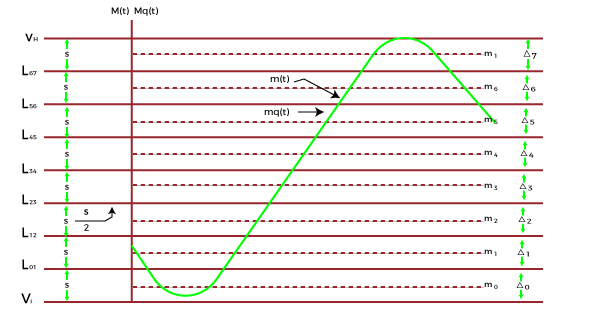
Quantization creates a series of discrete value from the analog signal. It separates the analog signal into N number of discrete sets. Each set has an equal size of S, which refers to the step size. It is given by: S = (VB - VA)/N Where, S is the step size VB is the upper limit of the given analog signal VA is the lower limit of the given analog signal N is the number of sets in which the analog signal range is divided Here, N = 8 The quantization levels are specified at the center of each step, as shown below: 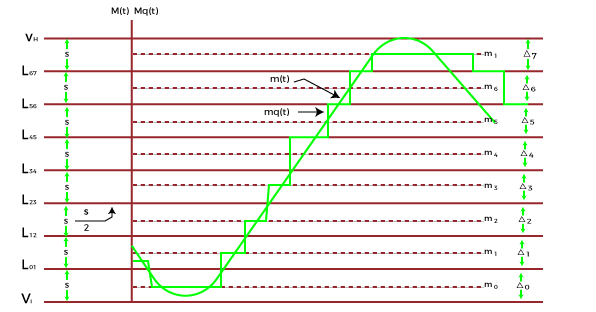
We know that the quantized signals are selected to approximate the original signals. The amplitudes of the discrete quantized levels are known as reconstruction levels. These levels are also named as representation levels. As discussed above, the distance between the two adjacent reconstructions level is defined as step size. Its quality can be improved by reducing the step size and increasing the number of quantization levels. A TV with 64 levels gives fair color quality, while a TV with 256 levels gives good color quality. The quantization levels are separated by 'S,' which is the step size. But, the distance of the extreme lower and upper quantization level from their nearest level is only S/2. As long as the instantaneous amplitude of the quantized signals is less than S/2, the noise will not appear at the output of the quantizer. Due to different components attached with the quantizer, such as repeater and amplifier, the quantized signal from the output of the quantizer comes with the removed noise. There are very low chances of quantization error to occur. Types of QuantizationThere are two types of Quantization, uniform Quantization and non-uniform Quantization. Uniform QuantizationAs the name implies, the quantized levels in the uniform quantization process are equally spaced. The uniform quantization is further categorized as mid-rise type uniform quantization and mid-tread type uniform quantization. Both the uniform quantization processes are symmetric about the respective axis. Mid-rise type uniform Quantization Rise refers to the rising part. The origin of the discrete quantized signal lies in the middle of the rising part of the stair like graph, as shown below: 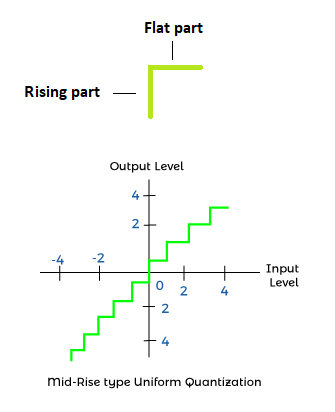
Mid-tread type uniform Quantization Tread refers to the flat part. The origin of the discrete quantized signal lies in the middle of the tread part of the stair like graph, as shown below: 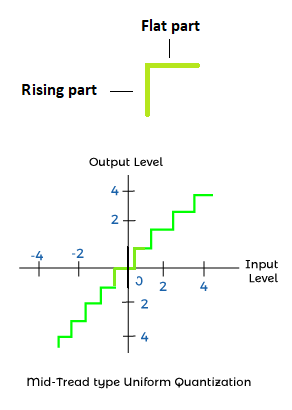
Advantages of Uniform QuantizationThe advantages of Uniform Quantization are as follows:
Non-uniform QuantizationThe quantized levels in the non-uniform quantization process are unequally spaced. The relation between such quantization is generally logarithmic due to non-linear nature of the signal. Advantages of non-uniform QuantizationThe advantages of non-uniform Quantization are as follows:
Quantization errorThe difference in the input value and the quantized value of the signal is known as the quantization error. The quantized signal (mq(t)) is the approximation signal of the message signal (m(t)). The difference between the message signal and the quantized signal is termed as quantized noise. It is given by: Qe = m(t) - mq(t) It depicts that the output of the quantization process or the received signal is not a perfect copy of the message signal. A noisy quantized signal is shown below: 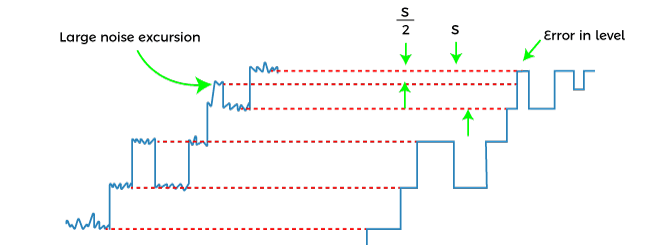
The same signal with removed noise is shown on the right side of the noisy signal. The repeaters help in the data transmission over long distances by increasing the signal power. We can decrease the attenuation suffered by the quantized signal be decreasing the space between the repeaters in the communication channel. It also decreases the noise power and error probability. Let's find the mean square quantization error represented as e2, where e is the voltage difference between the input and the quantized value. Here, the same concept of dividing the signal into M quantization levels will be used. The difference between each level is known as step size represent by S measured in volts. e = m(t) - mqv Where, E = voltage difference m(t) is the input message signal mqv is the output signal of the quantizer The greater the quantization levels, the smaller will be the step size. The mean square quantization error is given by: e2 = S2/12 Examples of QuantizerThe device used to perform the quantization process is known as quantizer. Let's discuss a common example of a quantizer. Analog to Digital ConverterA/D or Analog to Digital Converter consists of a sampler and quantizer. The function of the sampler is to convert a continuous time-varying signal to a discrete-time signal. The conversion process requires sampling and quantization to convert an analog signal to a digital signal. The quantizer function is to represent each level to the fixed discrete finite set of values. There are a number of available quantization bits, such as 8-bit, 16-bit, and 64-bit. The number of levels of each bit can be calculated using the formula (2n), where n refers to the bits. For the 8-bit, the number of quantization levels are 28 = 256 levels. For the 16-bit, the number of quantization levels are 216 = 65, 536 levels. For the 64-bit, the number of quantization levels are 264 = 16.8 million levels. The quantization noise inversely depends on the number of quantization levels. The greater the quantization levels, the lesser will be the quantization noise. Advantages of QuantizationThe advantages of quantization are as follows:
Applications of QuantizationApart from digital communication, quantization process is also used in various fields, such as signal processing, control systems, image processing, science, and linguistics.
CompandingCompanding is a type of non-uniform quantization and is used to increase the strength of the weak signals. It reduces the data rate of the input signal by varying the gap between the two adjacent quantization levels. The unequal quantization level makes it similar to the non-uniform quantization process. Companding is created from the combination of two words, compression and expanding. The signal is passed through the compressor at the transmitting end while it is passed through the expander at the receiving end. The compressor compresses the signal and improves the quality of transmission. But, it introduces distortion in the signal. The expander is used at the receiving end to undo the distortion introduced by the compressor. The inverse distortions of the two processes (compression and expanding) help in generating the output signal without distortion. The input-output characteristics of the expander are the reverse as compared to the compressor, as shown below: 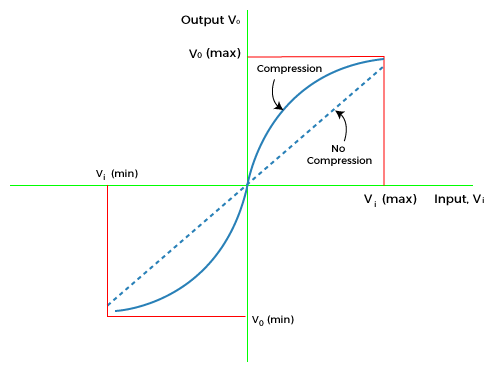
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










