Difference Between Quick Sort and Merge Sort

A sorting is the arrangement of collectively data in particular format like ascending or descending order. Generally, it is used to arrange the homogeneous data in sorted manner. Using the sorting algorithms, we can arrange the data in a sequence order and search an element easily and faster. Sorting techniques depends on two situation such as total time and total space required to execute a program. In this section, we will discuss quick sort and merge sort and also compare them each other.

Quick Sort

Quick sort is a comparison based sorting algorithm that follows the divide and conquer technique to sort the arrays. In quick sort, we usually use a pivot (key) element to compare and interchange the position of the element based on some condition. When a pivot element gets its fixed position in the array that shows the termination of comparison & interchange procedure. After that, the array divides into the two sub arrays. Where the first partition contains all those elements that are less than pivot (key) element and the other parts contains all those elements that are greater than pivot element. After that, it again selects a pivot element on each of the sub arrays and repeats the same process until all the elements in the arrays are sorted into an array.

Algorithm of Quick Sort

Partition (A, p, r)

1. X <- A[r]
2. I <- p-1
3. For j <- p to r -1
4. Do if A[j] <= x
5. Then I <- I + 1
6. Exchange A[i] <-> A[j]
7. Exchange A[I + 1] <--> A[r]
8. Return I + 1

Quicksort (A, p, r)

1. While (p < r)
2. Do q <- Partition (A, p, r)
3. R <- q-1
4. While (p < r)
5. Do q <- Partition (A, p, r)
6. P <- q + 1

Steps to sort an array using the quick sort algorithm

Suppose, we have an array X having the elements X[1], X[2], X[3],…., X[n] that are to be sort. Let's follow the below steps to sort an array using the quick sort.

Step 1: Set the first element of the array as the pivot or key element. Here, we assume pivot as X[0], left pointer is placed at the first element and the last index of the array element as right.

Step 2: Now we starts the scanning of the array elements from right side index, then

If X[key] is less than X[right] or if X[key] < X[Right],

1. Continuously decreases the right end pointer variable until it becomes equal to the key.
2. If X[key] > X[right], interchange the position of the key element to the X[right] element.
3. Set, key = right and increment the left index by 1.

Step 3: Now we again start the scanning of the element from left side and compare each element with the key element. X[key] > X[left] or X[key] is greater than X[left], then it performs the following actions:

1. Continuously compare the left element with the X[key] and increment the left index by 1 until key becomes equal to the left.
2. If X[key] < X[left], interchange the position of the X[key] with X[left] and go to step 2.

Step 4: Repeat Step 2 and 3 until the X[left] becomes equal to X[key]. So, we can say that if X[left] = X[key], it shows the termination of the procedures.

Step 5: After that, all the elements at the left side will be smaller than the key element and the rest element of the right side will be larger than the key element. Thus indicating the array needs to partitioned into two sub arrays.

Step 6: Similarly, we need to repeatedly follow the above procedure to the sub arrays until the entire array becomes sorted.

Let's see an example of quick sort.

Example: Consider an array of 6 elements. Sort the array using the quick sort.

arr[] = {50, 20, 60, 30, 40, 56}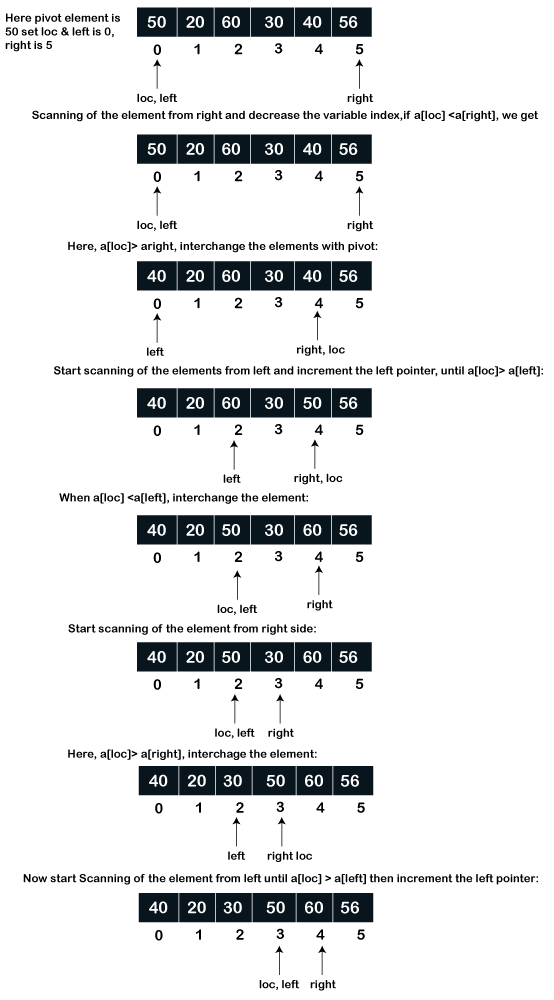

In the above array, 50 is in its right place. So, we divided the elements that are less than pivot in one sub array and the elements that are larger than the pivot element in another sub array.

Hence, we get the sorted array.

Let's implement the above logic in C program.

Quick.c

Output:

Sorted Array is:
Array = 50  20  60  30  40  56 

Merge sort

Merge sort is a most important sorting techniques that work on the divide and conquer strategies. It is the most popular sorting techniques used to sort data that is externally available in a file. The merge sort algorithm divides the given array into two halves (N/2). And then, it recursively divides the set of two halves array elements into the single or individual elements or we can say that until no more division can take place. After that, it compares the corresponding element to sort the element and finally, all sub elements are combined to form the final sorted elements.

Steps to sort an array using the Merge sort algorithm

1. Suppose we have a given array, then first we need to divide the array into sub array. Each sub array can store 5 elements.
2. Here we gave the first sub array name as A1 and divide into next two subarray as B1 and B2.
3. Similarly, the right sub array name as A2 and divide it into next two sub array as B3 and B4.
4. This process is repeated continuously until the sub array is divided into a single element and no more partitions may be possible.
5. After that, compare each element with the corresponding one and then start the process of merging to arrange each element in such a way that they are placed in ascending order.
6. The merging process continues until all the elements are merged in ascending order.

Let's see an example of merge sort.

Example: Consider an array of 9 elements. Sort the array using the merge sort.

arr[] = {70, 80, 40, 50, 60, 11, 35, 85, 2}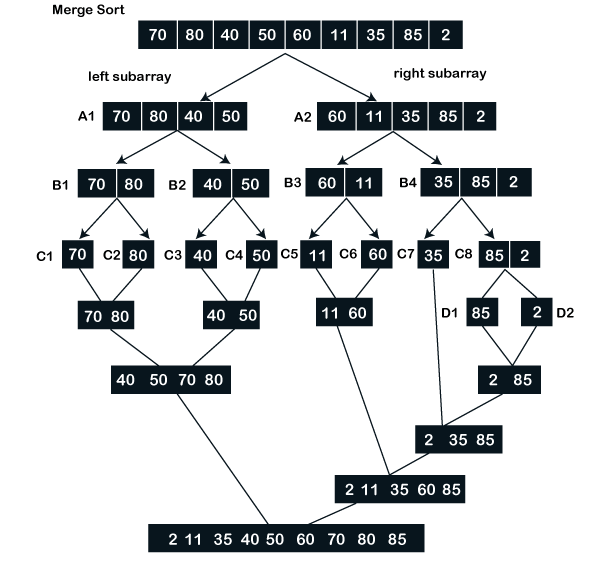

Hence, we get the sorted array using the merge sort.

Let's implement the above logic in a C program.

Merge.c

Output:

Predefined Array is
70      80      40      50      60      11      35      85      2

 Sorted array using the Merge Sort algorithm
2       11      35      40      50      60      70      80      85

Quick Sort vs. Merge Sort