Range Definition

Range definition refers to the set of values that a variable or function can take. In mathematics, range refers to the set of all possible output values of a function. In contrast, in statistics, range refers to the difference between a data set's maximum and minimum values. The range concept is important in various fields of study, including mathematics, statistics, economics, and engineering. This article will explore the concept of range definition in detail, including its different interpretations, applications, and limitations.

Range Definition in Mathematics

Collecting all potential output values of a function is called its range in mathematics. Consider the function f(x), which transfers an input set x to an output set y. The range of f(x) is the set of all possible values of y that can be obtained by applying the function to any input value x.

For example, consider the function f(x) = x^2, which maps every input value x to its square. The f(x) range is the set of all possible values of y that can be obtained by squaring any real number. Since every non-negative real number has a square root, the f(x) range is [0,∞).

Similarly, consider the function g(x) = sin(x), which maps every input value x to its sine. The range of g(x) is the set of all possible values of y that can be obtained by taking the sine of any real number. Since the sine function oscillates between -1 and 1, the g(x), the range is [-1,1].

Range Definition in Statistics

The difference between the highest and minimum values of data collection is the range in statistics. It is a straightforward metric of dispersion that reveals how dispersed the data is. The range is derived by subtracting the data set's minimum and highest values.

For example, consider the following data set: 2, 5, 7, 9, 10. The minimum value of this data set is 2, and the maximum is 10. Therefore, the range of this data set is 10 - 2 = 8.

The range is a useful measure of dispersion when the data set is small, and the distribution is roughly symmetric. However, it has some limitations, such as being sensitive to outliers and not considering the data distribution.

Applications of Range Definition

The concept of range definition has many applications in various fields of study. Here are some examples:

• Mathematics: In mathematics, range definition is used to describe the behavior of functions, such as their domain and range, and to solve problems involving optimization and calculus.
• Statistics: In statistics, range definition is used to measure the dispersion of data, along with other measures such as variance and standard deviation. It is also used to identify outliers and to compare the variability of different data sets.
• Economics: In economics, range definition is used to analyze the behavior of economic variables, such as prices, quantities, and incomes. It is also used to model economic relationships and to make predictions.
• Engineering: In engineering, range definition is used to design and optimize systems, such as control systems, communication systems, and mechanical systems. It is also used to model and analyze the behavior of physical phenomena, such as heat transfer, fluid mechanics, and structural mechanics.

Different Interpretations of Range

The concept of range can have different interpretations depending on the context in which it is used. The specific meaning of range may vary depending on the field of study and the type of data being analyzed. Now, we will explore some of the different interpretations of range and their applications in various fields.

• Range as the Set of Output Values of a Function

In mathematics, range refers to the set of all possible output values of a function. Consider a function f(x) that maps a set of input values x to a set of output values y. The f(x) range is the set of all possible values of y that can be obtained by applying the function to any input value x. For example, the range of the function f(x) = x^2 is [0, ∞), since every non-negative real number has a square root.

• Range as the Difference Between Maximum and Minimum Values

Range in statistics refers to the difference between a collection of data's maximum and minimum values. It is a straightforward dispersion measurement that shows how dispersed the data is. The range is obtained by deducting the minimum value from the greatest value of the data set. For example, the data set range {2, 5, 7, 9, 10} is 10 - 2 = 8.

• Range as the Interval of Values for a Variable

In mathematics and engineering, the range can also refer to the interval of values that a variable can take. For example, the range of the variable x in the equation y = mx + b is the set of all possible values of x that make the equation true. The range of a physical quantity, such as temperature or pressure, may also refer to the interval of values the quantity can take in a given system or environment.

• Range as the Spread of Data in a Distribution

The range can also describe the data spread in a distribution in statistics. For example, the range of a probability distribution is the difference between the maximum and minimum values of the distribution. The range can be used to compare different distributions' variability and identify outliers or unusual data points.

• Range as the Set of Values for a Categorical Variable

In statistics, the range can also refer to the set of values that a categorical variable can take. For example, the range of a variable, such as hair color or political affiliation, is the set of all possible values for that variable. The range of a categorical variable is often used to create frequency tables and other descriptive statistics.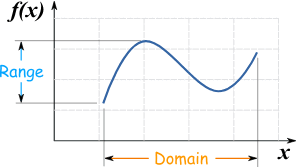

Limitation of Range

The range is a simple measure of dispersion widely used in statistics to describe the spread of a data set. While it can be a useful indicator of variability, it is important to understand its limitations and potential drawbacks when interpreting statistical data.

• Range Ignores the Distribution of Data

One of the main limitations of the range is that it ignores the distribution of data within the range. Range only considers the difference between the maximum and minimum values and does not consider how the data is spread out within that range. For example, a data set with a range of 10 could have a wide range of values with very little variation or a narrow range with high variation.

Consider the following two data sets:

Data Set 1: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Data Set 2: {1, 1, 1, 1, 1, 6, 6, 6, 6, 6}

Both data sets have a range of 9, but the first data set has a more uniform distribution of values, while the second data set has a bimodal distribution with two distinct clusters of values. Range alone cannot capture these differences in distribution.

• The range is Sensitive to Outliers

Another limitation of the range is that it is sensitive to outliers, which are data points significantly different from the rest of the data. Outliers can greatly impact the range, particularly if they are at one end of the data set. For example, consider the following data set:

Data Set 3: {1, 2, 3, 4, 5, 6, 7, 8, 9, 100}

The range of this data set is 99, which is largely driven by the outlier value of 100. However, the range does not accurately reflect the spread of most data points.

• Range Does Not Indicate the Central Tendency of Data

The range does not provide any information about the central tendency of the data, which is the typical or most common value in a distribution. For example, two data sets with the same range could have different means, medians, or modes. The range alone does not indicate which data set has a more typical value.

• The Range is Affected by the Sample Size

The sample size can also affect the range, particularly for small sample sizes. A small sample size may not represent the entire population and may result in a narrow range. In contrast, a large sample size may capture more variability and result in a wider range. It is important to consider the sample size when interpreting the range, particularly if it is small.

• Range is Limited in its Usefulness for Inferential Statistics

Range alone is insufficient for inferential statistics, which generalize a population based on a sample. Inferential statistics require more complex measures of dispersion, such as variance or standard deviation, to calculate confidence intervals and perform hypothesis tests. While range can provide some initial insights into the spread of the data, it is not sufficient for more complex statistical analyses.