Recaman's Sequence

Recaman's Sequence, named after the Colombian mathematician Bernardo Recaman Santos, is a fascinating integer sequence that has captured the imagination of mathematicians and computer scientists alike. It's defined by a simple yet intriguing rule, making it an excellent Java exploration topic.

Understanding Recaman's Sequence

Recamán's Sequence starts with the first term, which is always 0. Two rules determine the next term:

If the next term in the Sequence would be a positive integer not already in the Sequence, take that integer as the next term.

If the next term is negative or already in the Sequence, subtract that integer from the current term to get the next term.

Let's illustrate this with a few initial terms:

Start with 0 (the first term).
The next term would be 0 + 1 = 1.
The next term would be 1 - 2 = -1.
The next term would be -1 + 3 = 2.
The next term would be 2 - 4 = -2.
The next term would be -2 + 5 = 3.

Continue this process, always choosing the positive integer if it's not already in the Sequence.

The first few terms of Recaman's Sequence look like this: 0, 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, ...

General understanding of the rule

ds(0) = 0,
if(n > 0) and number is not in the Sequence
	ds(n) = ds(n-1 - n
else 
	ds(n) = ds(n-1) + n.

Java Implementation of the above approach depicts the computation of the next number using the recursive formula mentioned above

import 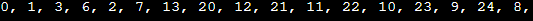java.util.Arrays;

public class RecamansSequence {
    
    // Method to print the first n terms of Recaman's Sequence
    static void generateRecamansSequence(int n) {
        // Create an array to store the terms
        int[] sequence = new int[n];

        // The first term of the Sequence is always 0
        sequence[0] = 0;
        System.out.print(sequence[0] + ", ");

        // Fill in the remaining terms using the recursive formula
        for (int i = 1; i < n; i++) {
            int curr = sequence[i - 1] - i;
            int j;
            for (j = 0; j < i; j++) {
                // If curr is negative or already exists in the Sequence
                if (sequence[j] == curr || curr < 0) {
                    curr = sequence[i - 1] + i;
                    break;
                }
            }
            sequence[i] = curr;
            System.out.print(sequence[i] + ", ");
        }
    }

    public static void main(String[] args) {
        int n = 17; // Number of terms to generate
        generateRecamansSequence(n);
    }
}

Output:

Time Complexity:

O(n^2). This is because the code potentially checks all previous terms for each term in the Sequence to ensure the next term is unique. This results in a nested loop structure, where for each of the n terms, it may perform up to n iterations in the worst case.

Space Complexity:

The space complexity of the code is O(n), where n is the number of terms in the Recamán's Sequence to be generated.

Optimized approach for the above principle

In this approach, we will make use of the hashing technique to store the previously computed values so that it reduces the time for computing values again and again

import 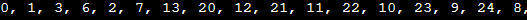java.util.HashSet;

public class RecamansSequence {
    
    // Method to print the first n terms of Recam�n's Sequence
    static void generateRecamansSequence(int n) {
        if (n <= 0)
            return;

        // Print the first term and store it in a HashSet
        System.out.print(0 + ", ");
        HashSet<Integer> seen = new HashSet<>();
        seen.add(0);

        // Initialize the previous term as 0
        int prev = 0;

        // Print the remaining terms using the recursive formula
        for (int i = 1; i < n; i++) {
            int curr = prev - i;

            // If curr is negative or already exists in the HashSet
            if (curr < 0 || seen.contains(curr))
                curr = prev + i;

            seen.add(curr);

            System.out.print(curr + ", ");
            prev = curr;
        }
    }

    public static void main(String[] args) {
        int n = 17; // Number of terms to generate
        generateRecamansSequence(n);
    }
}

Output:

Explanation:

In this approach, We define a method called generateRecamansSequence that takes an integer n as its input parameter. This n represents the number of terms we want in Recamán's Sequence.

Before diving into the sequence generation, we check if n is less than or equal to 0. If n is not a valid input (negative or zero), we return immediately since there are no terms to generate.

Next, we create a HashSet called seen. This HashSet will help us keep track of unique terms in the Sequence. We start with an empty set.

We initialize a variable prev to keep track of the previous term and start it at 0 since the first term of Recamán's Sequence is always 0.

Now, we enter a loop that iterates from the second term (i = 1) to the n-th term (i < n). We generate the terms one by one in this loop.

Inside the loop, we calculate the next term, curr, based on the previous term (prev) and the rules of Recamán's Sequence. We subtract i from prev to calculate curr.

However, we must ensure the contract is valid according to the rules. If curr is negative or already exists in our seen HashSet, we adjust it by adding i. This ensures that the term is unique and positive.

We then add curr to our seen HashSet to keep track of it and print it as part of the Sequence.

Finally, we update the previous variable to be equal to curr. This prepares us for the next iteration, where curr will become the previous term.

Time Complexity: O(n)

Space Complexity: O(n)

Next TopicThe sum of Elements Between k1th and k2th smallest elements

← prev next →