Recursion in Python

Pre-requisite knowledge: Functions in python

You might already know the meaning of the word "Recursion". According to Google, it means "The repeated application of a procedure or a definition,". It is the same in programming and is applied to the functions.

Any function that calls itself in its body repeatedly until a particular condition becomes false and the target task is done is called a "Recursive function" and this procedure is called "Recursion".

This article discusses how we follow Recursion with python functions.

To give a simple recap on functions, let us take an example:

#To check if a number is even or odd.
def evenORodd(num):
	if(num% 2 == 0):
		print("num is an even number")
	else:
		print("num is an odd number")
evenORodd(2)

Output:

num is an even number

Understanding:

Here, evenORodd is the function we defined to check if the given number, num, is an even or an odd number. We defined the function and then wrote the logic in it. Now, we want to check if 2 is even or odd, so we call the function by giving the argument as 2, which the function will replace at num and the function is carried on it.

When do we need to recurse a function?

When we want to perform a complex task, we generally break it into smaller tasks; doing them one after the other decreases the burden and the complexity. Just like this, when we need to write a code for a complex problem, we break it into smaller and repetitive parts.

For a simple example:

We need to write a program to find the factorial of a number. Suppose the user gave 6:

6! = 6 * 5 * 4 * 3 * 2 * 1

If we divide it:

6! = 6 * 5!

5! = 5 * 4!

4! = 4 * 3!

3! = 3 * 2!

2! = 2 * 1!

1! = 1

You can observe the repetition.

Formulating it:

N! = N * (N - 1)!

So, we write a function, say factorial for N, in which we call the same function again for N-1, which is repeated till N=1

Recursion or Iteration

Loops are used to perform repetitive tasks, and so are the functions? What is the difference, and how to know when to use what?

It is simple. When we use loops, we need to know how many times we need to iterate the loop as in a for loop. When we know the number of iterations, we use a for loop. If not, we will be left with either while and do-while loops or Recursion. We need to choose based on the need, and in some cases, we use Recursion for the return values.

Diving deep into recursion:

Syntax: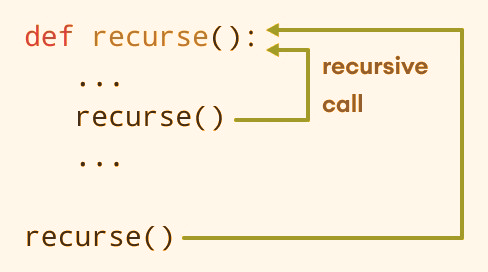

def function_name(arguments if any):
		#function body
		function_name(argument) #recursive call of the function

Let us take the Program of the previous code-Factorial of a number:

#function
def fact(num):
    if num == 1:
	return 1
   else:
           return (num * fact(num-1))
#Body of the program
num = int(input("Enter a number: "))
result = fact(num)
print("The factorial of the given number", num, "is", result)

Output:

Enter a number: 5
The factorial of the given number is 120

Understanding: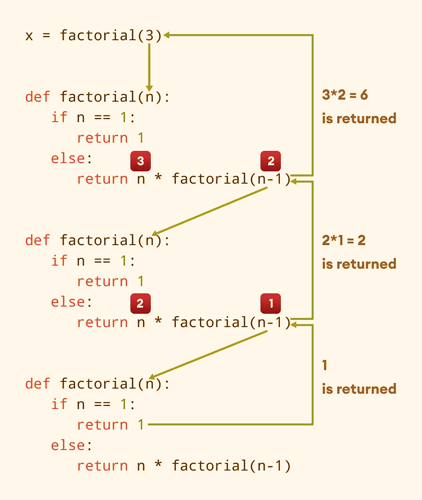

Fibonacci series:

The first two numbers are 0 and 1. We keep adding the previous two elements to get the next number, and this sequence of numbers is called the Fibonacci series.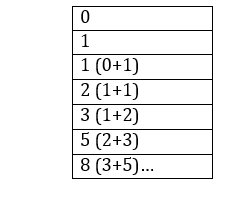

//To print the Fibonacci series till the given number of times
def fib(n):
	if num <= 1:
		return num
	else:
		return(fib(num-1) + fib(num-2))
num_terms = 10
if num_terms <= 0:
	print("The number of terms cannot be negative!!")
else:
	print("The Fibonacci series up to 10 terms:")
for i in range(num_terms):	
	print(fib(i))

Output:

The Fibonacci series up to 10 terms:
0
1
1
2
3
5
8
13
21
34

Understanding:

We need to print the Fibonacci series upto 10 numbers.

According to the loop in the program:

fib (0) = 0

fib (1) = 1

fib (2) = fib (1) + fib (0) = 1 + 0 = 1

fib (3) = fib (2) + fib (1) = 1 + 1 = 2

fib (4) = fib (3) + fib (2) = 2 + 1 = 3

fib (5) = fib (4) + fib (3) = 3 + 2 = 5

fib (6) = fib (5) + fib (4) = 5 + 3 = 8

fib (7) = fib (6) + fib (5) = 8 + 5 = 13

fib (8) = fib (7) + fib (6) = 13 + 8 = 21

fib (9) = fib (8) + fib (7) = 21 + 13 = 34

fib (10) = fib (9) + fib (8) = 34 + 21 = 55

We need 10 numbers. So, it takes only from 0 to 9.

//Program to find certain power of a given number
def pwr(num, power):
	if power == 0:
		return 1
    	else:
		 return num * pwr(num, power - 1)
pwr(2, 6)

Output:

Understanding:

Say, for the same sample input-pwr(2, 6):

2 * 2 * 2 * 2 * 2 * 2

Breaking it down:

pow(2,6) = 2 * pow(2, 5)

pow(2,5) = 2 * pow(2, 4)

pow(2,4) = 2 * pow(2,3)

pow(2,3) = 2 * pow(2,2)

pow(2,2) = 2 * pow(2,1)

pow(2, 1) = 2

So, we call the function for pwr(num, power) and then call it again for pwr(num, power-1) until power becomes 1, then pwr(num, 1) = num itself.

Tail-Recursion:

Any recursive function is called a tail-recursive function if the last task done by the function is executing a recursive call. In tail recursion, the function returns only a call to itself-nothing more than that.

Difference between normal Recursion and tail-recursion:

Let us take an example:

Here is a code to calculate the sum of first "num" natural numbers:

def sum(num):
    if (num === 0):
        return 0
    else:
        return num + sum(num - 1)

What happens here is simply:

sum (5)

5 + sum (4)

5 + (4 + sum (3))

5 + (4 + (3 + sum (2)))

5 + (4 + (3 + (2 + sum (1))))

5 + (4 + (3 + (2 + (1 + sum (0)))))

5 + (4 + (3 + (2 + (1 + 0))))

5 + (4 + (3 + (2 + 1)))

5 + (4 + (3 + 3))

5 + (4 + 6)

5 + 10

The interpreter has to remember the values of all the variables and the calls until the Program's end. It needs to remember the value of num to keep multiplying with the recursive function call.

Now, look at this code:

def sum(num, total = 0):
   	 if (num === 0):
        		return total
     	else:
        		return sum(num - 1, total + num)

Mechanism here:

sum(5, 0)

sum(4, 5)

sum(3, 9)

sum(2, 12)

sum(1, 14)

sum(0, 15)

The interpreter need not remember the values of any variables outside the function calls. It can just forget them and concentrate on the recursive function calls. As you can see, it only returns a function call and nothing more than that.

IT MATTERS BECAUSE:

These types of functions (Tail Recursive functions) can be optimized and used efficiently by the compiler. Non-tail recursive functions, on the other hand, cannot be optimized by the compiler.

When we execute a recursion code, the compiler generally uses a stack to store the values like parameter values during each recursive call. It pushes all the new values into the stack when it comes through a recursive call. It keeps happening till the end of the function. Then, all the values are popped out.

In a non-tail recursive function, the stack depth will be more as it contains more values to be remembered by the compiler. In the case of the tail recursion, it need not keep the current function call's stack frame. The stack pops it out.

As shown in the above natural numbers example, we convert non-tail recursive functions to tail recursion functions to seek optimization from the compiler.

Here is the factorial function converted:

#Non-tail Recursion
def Fact(num): 
            if (num == 0): 
                        return 1
            return num * Fact(num-1) 

You may think this looks like a tail recursive function. But it is not. There is an additional multiplication with num to the function call in the return statement. We need the function call alone in the return statement.

#Tail recursion
def Fact(n, recur_factval = 1): 
                if (n == 0): 
                           return recur_factval 
               return Fact(n - 1, n * recur_factval) 

This is the converted tail-recursion code for the factorial of a given number.

Advantages and disadvantages of Recursion:

Advantages	Disadvantages
The logic and the code will be easier to write	Using recursive functions makes the code slower than using non-recursive functions
We solve some problems naturally using Recursion, like the Hanoi tower	These functions consume more memory to hold the variables and values between function calls in the stacks.
Makes the code straight-forward and reduces unnecessary function calls in the Program	Sometimes, for a first time viewer or a programmer, the code may seem complex and hard to understand
Reduces the length of the Program.	Not much efficient in terms of space and time complexities.

Using Recursion is extremely useful in solving problems in data structures and stacks evolutions. But, at the same time, if the calls are not checked properly, the memory will be wasted a lot, and the computer might even run out of memory.

Having advantages and disadvantages, too, Recursion is used based on the need of the problem and is a quite important and useful mechanism in python programming.

Next TopicReal-Time Data Analysis from Social Media Data in Python

← prev next →