Red Black Tree vs AVL tree

Before understanding the Red-Black tree and AVL tree differences, we should know about the Red-Black tree and AVL tree separately.

What is a Red-Black tree?

The Red-black tree is a self-balanced binary search tree in which each node contains one extra bit of information that denotes the color of the node. The color of the node could be either Red or Black, depending on the bit information stored by the node.

Properties

The following are the properties associated with a Red-Black tree:

The root node of the tree should be Black.
A red node can have only black children. Or, we can say that two adjacent nodes cannot be Red in color.
If the node does not have a left or right child, then that node is said to be a leaf node. So, we put the left and right children below the leaf node known as nil

The black depth or black height of a leaf node can be defined as the number of black that we encounter when we move from the leaf node to the root node. One of the key properties of the Red-Black tree is that every leaf node should have the same black depth.

Let's understand this property through an example.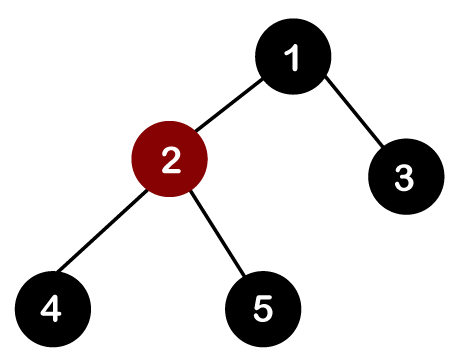

In the above tree, there are five nodes, in which one is a Red and the other four nodes are Black. There are three leaf nodes in the above tree. Now we calculate the black depth of each leaf node. As we can observe that the black depth of all the three leaf nodes is 2; therefore, it is a Red-Black tree.

If the tree does not obey any of the above three properties, then it is not a Red-Black tree.

Height of a red-black tree

Consider h as the height of the tree having n nodes. What would be the smallest value of n?. The value of n is the smallest when all the nodes are black. If the tree contains all the black nodes, then the tree would be a complete binary tree. If the height of a complete binary tree is h, then the number of nodes in a tree is:

n = 2h -1

What would be the largest value of n?

The value of n is largest when every black node has two red children, but the red node cannot have red children, so that it will have black children. In this way, there are alternate layers of black and red children. So, if the number of black layers is h, then the number of red layers is also h; therefore, the tree's total height becomes 2h. The total number of nodes is:

n = 2*2h-1

What is the AVL tree?

An AVL tree is a self-balancing binary search tree if we observe the below case, which is a binary search tree and a balanced tree.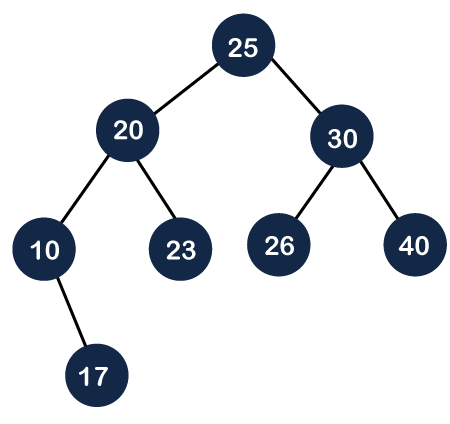

In the above tree, the worst-case time complexity for searching an element is O(h), i.e., the height of the tree. In the above case, the number of comparisons made to search 17 element is 4, and the height of the tree is also 4.

If we consider the skewed binary tree, as shown below: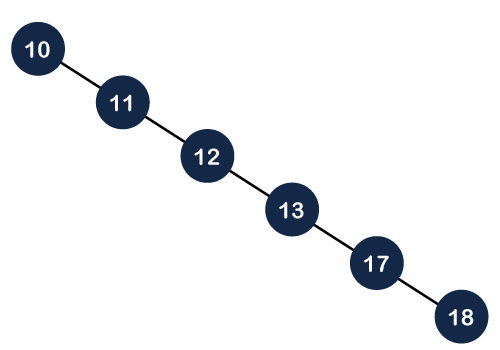

In the above right skewed tree, the number of comparisons made to search 17 element is 5, and the number of elements present in the tree is also 5. Therefore, we can say that if the tree is a skewed binary tree then the time complexity would be O(n).

Now, we have to balance these skewed trees so that they will have the time complexity O(h). There is a term known as a balance factor, which is used to self -balance the binary search tree. The balance factor can be computed as:

Balance factor = height of left subtree-height of right subtree

The value of the balance factor could be either 1, 0 or -1. If each node in the binary tree is having a value of either 1, 0, or -1, then that tree is said to be a balanced binary tree or AVL tree.

The tree is known as a perfectly balanced tree if the balance factor of each node is 0. The AVL tree is an almost balanced tree because each node in the tree has the value of balance factor either 1, 0 or -1.

Differences between the Red-Black tree and AVL tree.

The following are the differences between the Red-Black tree and AVL tree:

Binary search tree

The Red-Black tree is a binary search tree, and the AVL tree is also a binary search tree.

Rules

The following rules are applied in a Red-Black Tree:

The node in a Red-Black tree is either red or black in color.
The color of the root node should be black.
The adjacent nodes should not be red. In other words, we can say that the red node cannot have red children, but the black node can have black children.
There should be the same number of black nodes in every path; then, only a tree can be considered a Red-Black tree.
The external nodes are the nil nodes, which are always black in color.

Rule of the AVL tree:

Every node should have the balance factor either as -1, 0 or 1.

Example

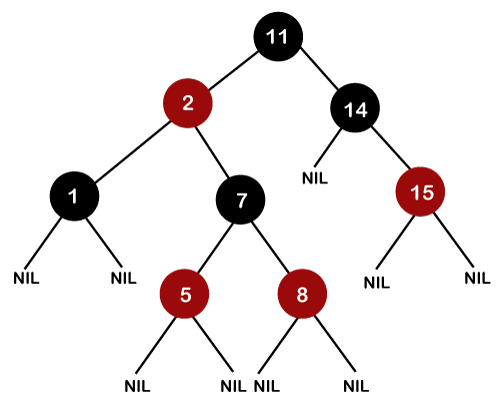
In the above figure, we need to check whether the tree is a Red-Black tree or not. In order to check this, first, we need to check whether the tree is a binary search tree or not. As we can observe in the above figure that it satisfies all the properties of the binary search tree; therefore, it is a binary search tree. Secondly, we have to verify whether it satisfies the above-said rules or not. The above tree satisfies all the above five rules; therefore, it concludes that the above tree is a Red-Black tree.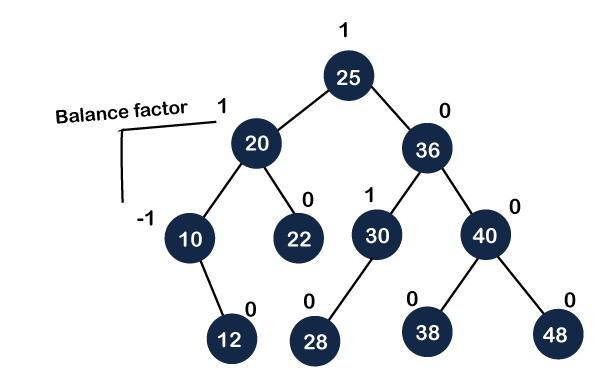

In the above figure, we need to check whether the tree is an AVL tree or not. As each node has a value of balance factor either as -1, 0, or 1, so it is an AVL tree.

How can the tree be considered as a balanced tree or not?

In the case of a Red-Black tree, if all the above rules are satisfied, provided that a tree is a binary search tree, then the tree is said to be a Red-black tree.

In the case of the AVL tree, if the balance factor is -1, 0, or 1, then the above tree is said to be an AVL tree.

Tools used for balancing

If the tree is not balanced, then two tools are used for balancing the tree in a Red-Black tree:

Recoloring
Rotation

If the tree is not balanced, then one tool is used for balancing the tree in the AVL tree:

Rotation

Efficient for which operation

In the case of the Red-Black tree, the insertion and deletion operations are efficient. If the tree gets balanced through the recoloring, then insertion and deletion operations are efficient in the Red-Black tree.

In the case of the AVL tree, the searching operation is efficient as it requires only one tool to balance the tree.

Time complexity

In the Red-Black tree case, the time complexity for all the operations, i.e., insertion, deletion, and searching is O(logn).

In the case of AVL tree, the time complexity for all the operations, i.e., insertion, deletion, and searching is O(logn).

Let's understand the differences in the tabular form.

Parameter	Red Black Tree	AVL Tree
Searching	Red Black tree does not provide efficient searching as Red Black Trees are roughly balanced.	AVL trees provide efficient searching as it is strictly balanced tree.
Insertion and Deletion	Insertion and Deletion are easier in Red Black tree as it requires fewer rotations to balance the tree.	Insertion and Deletion are complex in AVL tree as it requires multiple rotations to balance the tree.
Color of the node	In the Red-Black tree, the color of the node is either Red or Black.	In the case of AVL trees, there is no color of the node.
Balance factor	It does not contain any balance factor. It stores only one bit of information that denotes either Red or Black color of the node.	Each node has a balance factor in AVL tree whose value can be 1, 0, or -1. It requires extra space to store the balance factor per node.
Strictly balanced	Red-black trees are not strictly balanced.	AVL trees are strictly balanced, i.e., the left subtree's height and the height of the right subtree differ by at most 1.