Regular Grammar in Discrete MathematicsThe regular languages can be generated by regular grammar. In regular grammar, the left-hand side always consists of a single non-terminal. The left side cannot have more than one non-terminal or any terminal variable. There can be a single terminal or a single terminal followed by a non-terminal on the right-hand side. The production of regular grammar will be in the following form: Where X and Y are used to indicate the Variable (V). 'x' is used to indicate the string of terminals (T*) Types of Regular GrammarThere are two types of regular grammar, which are described as follows:
Left Linear GrammarThe production must be in the following form in the left linear grammar. Where X, Y belongs to a variable (V), and 'x' belongs to T*. Right Linear GrammarThe production must be in the following form in the right linear grammar. Where X, Y belongs to a variable (V), and 'x' belongs to T*. The regular language can be described as a language that is generated by the type 3 grammar and for which finite automata can be designed. It is able to convert FA into type 3 grammar. Example: In this example, we will show the finite automata accepting a string that begins with the symbol y. 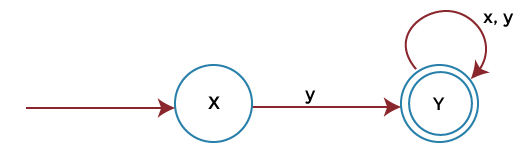
The right linear grammar corresponding to FA is described as follows: As we can see that the above grammar is right-linear grammar. This grammar can be written directly through finite automata. 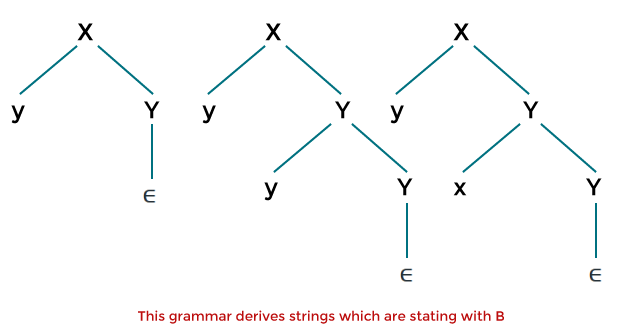
A string can be generated with the help of above RLG, which begins with b. After that b, this string can accept any input symbol (i.e., ∑ = {x, y}). We will get the following grammar if we reverse the production of above right linear grammar (RLG): This grammar derives the language that has all the strings that end with b, which is described as follows: In conclusion, we can say that suppose we have finite automata which represent language L, and we convert it into the right linear grammar, which also represents the same language L. In this case, when we reverse the RLG (right linear grammar), we will get the left linear grammar representing language L', which is the reverse of L. Conversion of RLG into LLGThe following steps will be used when we convert the right linear grammar into the left linear grammar for language L. Step 1: For language L, we have to reverse the FA (Finite automata). Step 2: After that, we have to write the right linear grammar for it. Step 3: Now, we will reverse the RLG. After step 3, we will get the grammar that generates the language, which is able to represent the left linear grammar for the same language L. 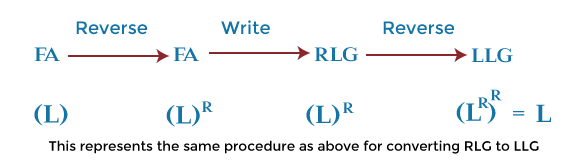
Here L is used to describe the language for FA (finite automata), and LR is used to describe the reversal of language L. Example: In this example, we will use the above finite automata representing language L, and accept all the string that begins with the symbol y. This language contains input symbol (i.e., ∑ = {x, y}). Here we will convert this automata into the left linear grammar. Solution: Step 1: The reversal of finite automata is described as follows: 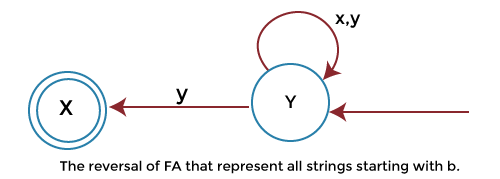
Step 2: For this reversal FA, the corresponding right linear grammar is described as follows: Step 3: Now we will reverse the above right linear grammar and get the following grammar: So this grammar is left linear grammar, which is used to represent all string that begins with the symbol y. So Conversion of RLG (Right linear grammar) to FA (Finite automata):We will begin from the first production. From every left variable/alphabet, we will go to the symbol followed by it. Start state: The first production state is known as the start state. Final state: All the states which end up with terminals without following any further non-terminal. Example: In this example, we have the right linear grammar for language L. This grammar shows all the strings which end with 0. So the finite automata which correspond to right linear grammar are described as follows: Here we will begin with variable X and use its production like this:
So for the corresponding right linear grammar, the final NFA (nonfinite automat) is described as follows: 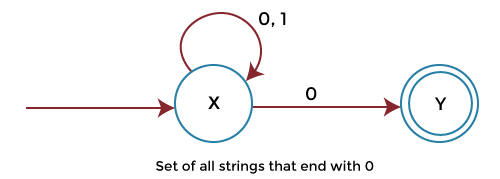
Conversion of LLG to FA: 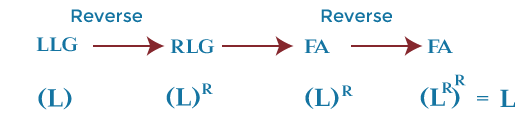
Explanation: Here we have first converted the LLG into the RLF grammar. Here LLG (Left linear grammar) represents the language L, which RLG (Right linear grammar) represents the reversal of language L, i.e., LR. After that, we will design the FA corresponding to this reversal language (LR). After that, we will reverse the finite automata (FA). The reversal FA is the final FA for language L. Conversion of LLG into RLG To explain this, we will take the above grammar, which is used to represent the language L, and accept all sets of strings that begin with variable y. The left linear grammar for this grammar is described as follows: Step 1: In this step, we will convert the LLG into FA. There is the same process of conversion as described above. So 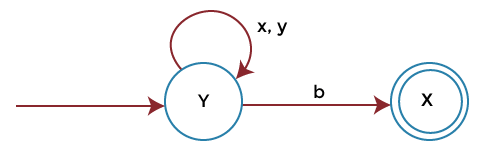
Step 2: In this step, we will reverse the FA. That means we will convert the initial state into the final state and the final state into starting state. We will also reverse all the edges like this: 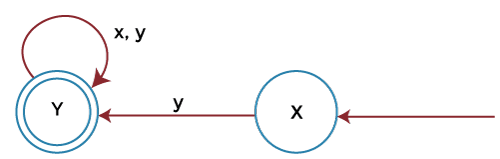
Step 3: In this step, we will write RLG corresponding to reversed finite automata. 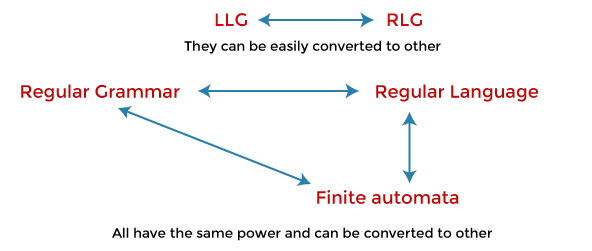
Next TopicPrime Number in Discrete Mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










