Right Angle- DefinitionRight angles are angles that are exactly 90 degrees. The proper angles are frequently demonstrated in everyday life. For instance, the edges of the cardboard or the corner of a book. Any form that is square or rectangular will have corners that are right angles or 90 degrees. Hence, a 90-degree angle is a right angle. An angle is a figure that is created in geometry by two rays that share a vertex and are referred to as the sides of the angle. Angles formed by two rays are in the plane where the rays are located. Angles can also be created when two planes intersect. The measure of an angle or a rotation is also referred to as an angle. Several angles are defined based on this rotation. One will discover one of these angles in this article along with detailed illustrations. Right Angle definitionThe angle formed by two lines that are perpendicular to each other is called a right angle. A right angle is equal to 90° and is in the shape of the letter "L". What is a Right Angle?It is referred to as a right angle if the angle formed by two rays exactly equals 90 degrees, or /2. Angles less than 90°, such as 87°, 56°, 77°, and 42°, are referred to as acute angles, whereas angles greater than 90°, such as 91°, 98°, 102°, 150°, and 167°, are referred to as obtuse angles. Right angles can be expressed as 90 degrees in degrees and as /2 (= 1.5708 radians) in radians. 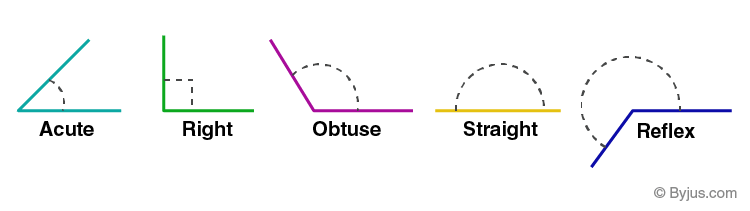
Right Angle shapeThe shape of a right angle created by two rays is depicted in the figure below. It appears to be the letter "L". 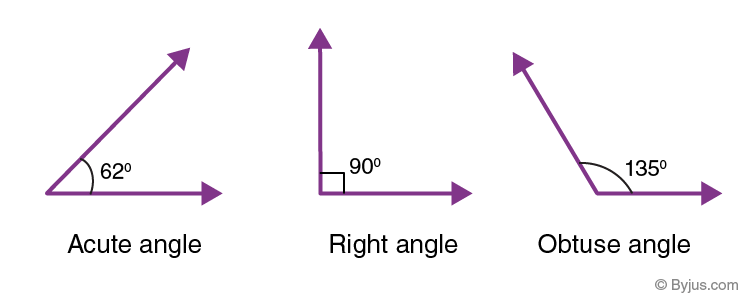
Like this, there are a few real-world instances of objects with right angles all around us.
Right Angle triangleThe base, hypotenuse, and perpendicular are the three sides of a right-angled triangle, and the angle between the base and perpendicular is 90°. One of the fundamental geometric shapes, the right-angled triangle serves as the basis for trigonometry. 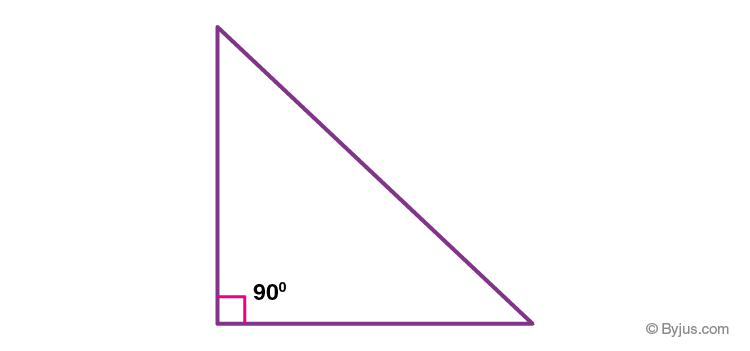
The longest side in a right triangle, or hypotenuse, is located on the other side of the triangle's right angle. Right Angle triangle formulaThe Pythagoras theorem is the formula used to determine whether a triangle is a right triangle or not. According to the theory, the hypotenuse's square is equal to the sum of its two other side's squares. (Hypotenuse)2 = (Base)2 + (Perpendicular)2 Right Angle triangle propertiesThe following is a summary of some of a right triangle's crucial characteristics:
Triangle with a right angleThe triangle's area is the region that a triangle's three sides in a plane enclose. The equation to determine the area of a right triangle is given by. Area (A) = = ½ × Base × Height Here, Height = Perpendicular Right Angle isosceles triangleRight triangles are classified as isosceles when their base and perpendicular sides, which make up the other two sides except the hypotenuse, are congruent. The base and angle perpendicular to the hypotenuse of this kind of triangle are congruent, or each measure 45 degrees. Right Angle examplesWe may see right angles in a variety of items, such the corners of classroom boards and the edges of a book that meet at right angles at their vertices. The rectangular board with right angles at its corners is depicted in the figure below: 
We are aware that a square's internal angles are all right angles, or 90 degrees, as illustrated in the image. 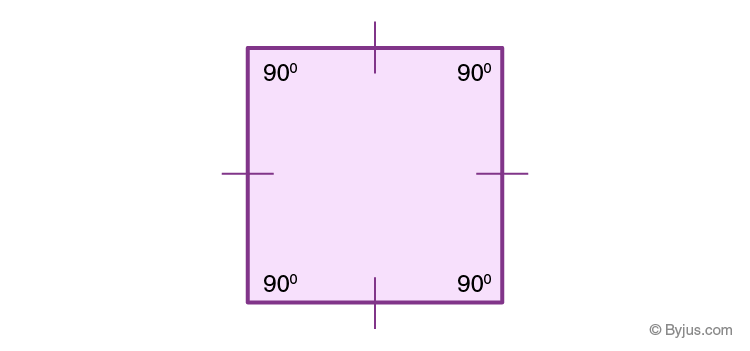
Next TopicSample Definition
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










