Rotation Definition

We are aware that in reality both the Earth and the moon spin on their own axes. So what exactly is rotation? The four fundamental forms of transformations that are worked with by geometry are rotation, reflection, translation, and resizing. We will learn about the basic idea of rotation in this article.

An object moving in a circular manner around its center or another axis is referred to be rotation. An object may spin around any limited number of imaginary axes or lines. As an object rotates, every component of the object moves around the axis at the same speed. Rotation is one of the four different types of transformations in general. Compared to linear motion, rotational motion is more complicated.

Objects can be turned in either a clockwise or anticlockwise direction, and at various angles. The angle of rotation is seen negatively when it is in the clockwise direction and positively when it is in the anti-clockwise direction.

The picture below shows an object rotated both clockwise and anticlockwise via various angles.

Let's examine the rotational formula

Formula for Rotation

We are aware that rotation can occur both clockwise and anticlockwise. The circular movement of a figure around a fixed point, notably the origin, is referred to as rotation in mathematics. As a result, the coordinates of the rotated point or figure change. Any angle can be used for the rotation. As the object is rotated about the origin, let's look at the rotation formula for a few typical angles in both directions.

Moreover, there is a generic rotation formula that may be used if the rotation is not about the origin but rather around a point Q(α, β) as shown below:

Let the point's starting coordinates be (x, y). Then, using the formula, the coordinates of the point after rotation (x', y') around point Q

(x', y') = {α + (x-α)cosθ - (y-β)sinθ, β + (x-α)sinθ - (y-β)cosθ}

Matrix Rotation

In Euclidean space, rotation is possible with the use of a rotation matrix. The matrix rotates a point by an angle anticlockwise and outputs the coordinates of the point in the Cartesian Plane after that rotation. It is possible to represent the rotation matrix R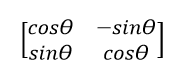

A point represented by vector V can therefore be multiplied by this matrix as follows: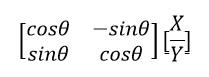

Rotational Symmetry

Due to the figure's rotational symmetry, its shape doesn't change when rotated relative to its initial form. These figures are considered to have rotational symmetry because they have an axis of symmetry. There are several approaches to finding rotational symmetry. The simplest method is starting the item's rotation from 0° to 360°.

An item is considered to have rotational symmetry at that angle of rotation if its shape remains the same during rotation relative to its original form. For example, a circle has rotational symmetry at all angles, a square has rotational symmetry when rotated through multiples of 90?, and a triangle has rotational symmetry.

Examples of the Rotational Formula Solved

Example 1: Rotate 90 degrees clockwise and get the coordinates of the point (7, 4) that results.

Solution: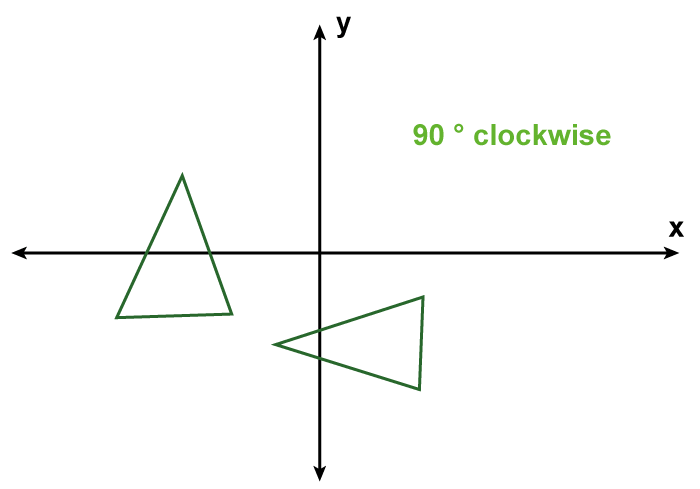

(X, Y) = given (7, 4)

The coordinates are given after turning the position 90° clockwise (y, -x)

Hence, the point's coordinates upon rotation are (4, -7).

Example 2: Rotate 180 degrees anticlockwise and get the coordinates of the point (3, 4) that results.

Solution: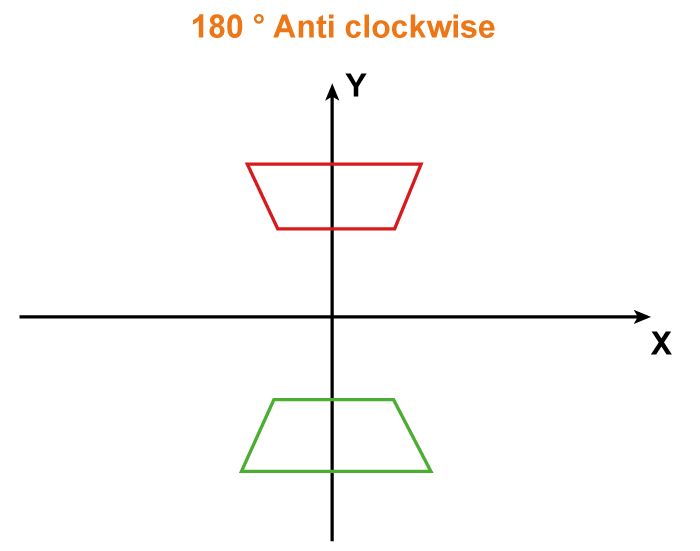

(X, Y) = given (6, 8)

The coordinates are provided using after the location has been rotated 180° anticlockwise (-x, -y)

Hence, the point's coordinates upon rotation are (-6, -8).

Example 3: After rotating 270 ° clockwise, the coordinates of the point (x, y) are (5, 7). What are the point's exact coordinates?

Solution: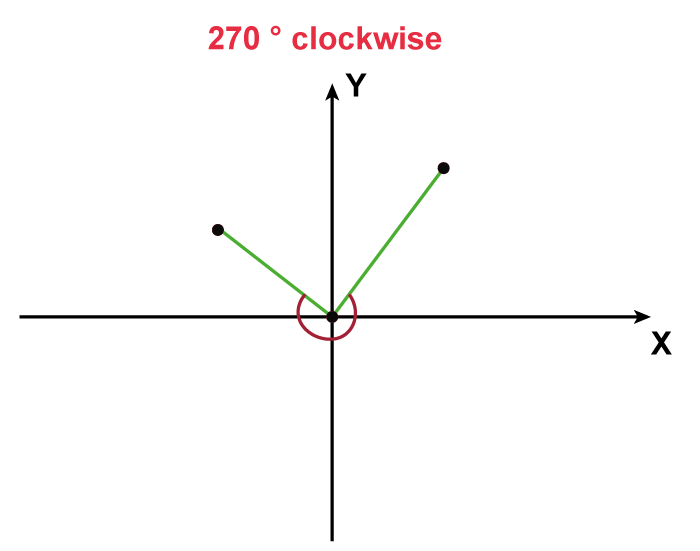

beginning coordinates are given (x, y)

Following rotation, the final coordinates are (5, 7). After rotating 270 ° anticlockwise, the absolute coordinates are known to be given by (-y, x).

Therefore (-y, x) = (5, 7)

So (x, y) = (7, -5)

Hence, the point's exact coordinates are (7, -5).

Example 4: After rotating 90 degrees anticlockwise, get the coordinates of the point (1, -6).

Solution: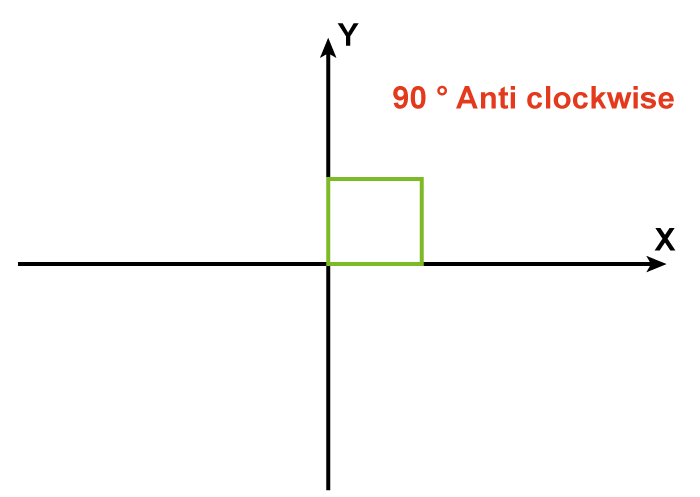

(X, Y) = given (2, -4)

The coordinates are obtained by turning the position 90° clockwise (-y, x)

Hence, the point's coordinates upon rotation are (4, 2).

Rotation-Related Frequently Asked Questions

Question 1: What is the point of rotation?

Answer: The direction along which a body is rotated is known as the point of rotation.

Question 2: Provide some examples of rotation.

Answer: Some examples of rotation include:

• Earth's rotation on its axis.
• Fan motion.
• Any globe's rotation on its axis.

Question 3: What does an angle of rotation mean?

Answer: The angle of rotation is the amount of course expressed in degrees.

Question 4: What exactly does the term "rotation" mean?

Answer: A form of transformation is rotation, which is the circular motion of an object about a fixed point, axis, or center.

Question 5: Write about the three different forms of rotation.

Answer: There are three different rotations:

• Nutation
• Precession
• Fundamental Rotation