RSA Encryption in Discrete Mathematics

RSA stands for Rivest Shamir Adleman. It can be described as an encryption algorithm, which is used to securely transfer the message with the help of internet. The principle behind this algorithm is that we can easily multiply a large amount of numbers, but it will be difficult to factor the large numbers. For example, when we multiply the 31 and 37, we can easily get the result 1147, but it is a very long process to determine the factorial of 1147.

RSA is a type of public-key cryptography. Public key cryptography requires two keys. One key will be used to decrypt the message, and the second key will be used to encrypt the message. This means that the one key will be made public key, and the second key will be secret from everyone. The second key can also be called a private key.

There are various types of public-key cryptography, but the most famous one is RSA. The RSA is totally based on the number theory. The RSA can be used in file encryption, secure shell or ftp, sending information of credit card/ debit card, saving passwords, encrypting e-mails, and many more.

Example 1: The message we are trying to send the owner can be encrypted by anyone with the help of a public key, but it can be decrypted only by the owner with the help of a private key. It shows like we have a private lock box that contains a slot for the message.

There can be an opposite case where the owner encrypts the message with the help of their private key, and anyone has the ability to decrypt it. But in this case, only the owner can encrypt the message.

Example 2: Suppose a student of COMPSCI 2 wants to send the solution of their homework on Piazza for Harry to read them, and at the same time, he doesn't want the other students to read their solution. Now we have to determine how Harry can easily enable every person to use a public channel to send him secrets in a way that nobody else can read.

Solution: The process will be very long if we try to set up a separate channel for correspondence's each pair. That means it will be lengthy if we use to encrypt a message with the help of a public key and decrypt it with the help of a private key.

The situation is asymmetric: Everybody who is on Piazza can send the message to Harry. The cipher can be read by anyone, but only the sender (COMPSCI 2), and Harry is able to read the clear text of each message.

To more understand this example in the real world, we can replace Harry with the bank, homework with the credit card number, and students with customers. So everyone who has a bank account, and sends the message to bank. The other customer can only know that some customer has a credit card of this bank, but the credit card details are only contained by the bank and that customer.

Generating of RSA keys:

The following steps will be used to generate the public key or private key pair in RSA:

1. Suppose there is a pair p and q, which indicate large random prime numbers and contain the same amount of bits. We have to generate these p and q.
2. Now, we have to compute the n in the following form:
   n = pq
   Here modules are indicated by the public integer n.
3. Now, we will select an odd public exponent e that is relatively primed to the following terms: (p - 1) (q - 1) and 1 < e < (p - 1) (q - 1)
4. Now, we have to compute the p, q, and a private exponent d.
5. The Private keys will be calculated by the pair (n, d), and Public keys are indicated by the pair (n, e).

Questions related to Key generation:

There are some questions related to key generation, which are described as follows:

Question 1: Suppose we have Φ, and we have to determine the e such that 1 < e < Φ and GCD (Φ, e) = 1

Solution: As we can see, e is smaller than Φ and greater than 1, and co-prime with Φ.

So here we will try primes, and we have to be careful that these primes do not divide Φ.

Question 2: Suppose we have e and Φ, and we have to determine d such that d ⋅ e ϕ = 1

Solution: To solve this, we have a solution. So we can use an extension of Euclid's GCD algorithm

Working Scenario of RSA

Suppose Alice wants to send the office files to Bob. She will post the grades on Piazza, but at the same time, she doesn't want that the other students will read them. So for this, Alice and Bob need a cryptosystem. Here Bob has both the keys: Public key and private key. So Bob will set up the private key and public key for their office privacy. The public key (n, e) will be set as (3233, 17), and the private key (n, d) as (3233, 2753). He will keep 'd' secret and posts 'n' and 'e' on piazza.

Here Alice encrypts the message with the help of Bob's public key. Alice also doesn't know the private key d. After all, someone could intercept that if Bob were to send it to Alice. Bob is able to decrypt the message with the help of their own private key. We can only encrypt the message with the help of a public key, but we cannot decrypt it. So, in this case, anyone who is on Piazza is able to send the message to Bob. But the clear text of each message can be read by the sender and Bob.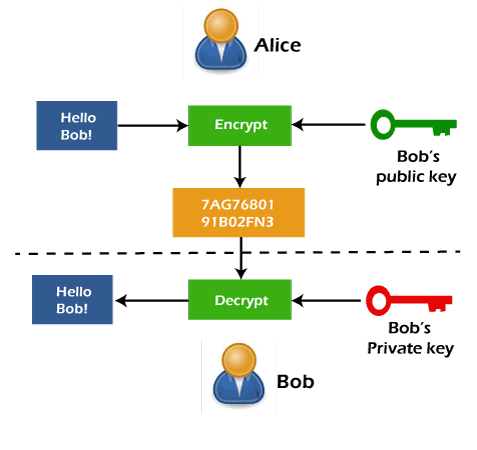

RSA Encryption

The encryption is used to secretly send the message. We can encrypt a message which is encoded as an integer with the help of following ways:

First, we will translate each letter into an integer. After that, we will form a larger integer by grouping these integers. A block of letters will be represented by these larger integers. Each block can be encrypted with the help of following mapping:

In other words, the encryption operation of RSA can be described as exponentiation to the e^th power module n in the following form:

Here c is used to indicate the resulting ciphertext, and input m is used to indicate the message. In practice, the message m can be described as some kind of appropriate formatted key that will be shared. With the help of a traditional encryption algorithm, the actual message can be encrypted with the shared key. With the help of this construction, we are able to encrypt a message of any length with only one exponentiation.

For example:

Suppose Anne wants to send a message "gcd" to Chris. For this, she will encode this message into a positive integer m, which must be smaller than the module n = 3233.

If the message is longer, then it will be broken into chunks. The transformation will be reversible. In this example, there will be two-character chunks and maximum 9 characters in the alphabet, which is described as follows:

Here the underscore is used to indicate the padding. It is obviously reversible. Till now, nothing is secret or mysterious. We will encrypt and separately send 73 and 40. First, we will send m = 73, and after that, we will send m = 40.

Working of RSA Encryption

Here Message m = 73, Public key (n, e) = (3233, 17).

When we encrypt a message, it will generate cipher text like this:

c = m^e MOD n

After putting the values, we will get the following

c = 7317 MOD 3233

c = 4747758526700098686074966922953 MOD 3233 = 1486

As we can see that the final result is small, but the intermediate result is huge. We can fix that with the help of pow. Now post the result of c (ciphertext), which is 1486 on Piazza.

Example of RSA Encryption:

In this example, we have to use RSA to encrypt the message "STOP" with p = 43, q = 59, and e = 13.

Solution:

1. We have to first determine n with the following formula:
   n = p * q
   n = 43 * 59 = 2537
2. After that, we have to convert each letter into a number in [0, 25].
   S = 18, T = 19, O = 14, P = 15.
3. Now, we have to group the sequence into the blocks of 4 digits, which is described as follows:
   m = 1819 1415
4. Now, we will encrypt each block with the help of formula:
   c = m¹³ (mod 2537)
5. Now, we have to first determine the first block like this:
   1819¹³ = mod 2537 = 2081
6. Now, we have to determine the second block like this:
   141513 = (mod 2537) = 2182

So the Ciphertext c = 2081 2182