Sampling

Sampling in statistics or research is defined as a method to select a subset from the large data. In digital communication, it is defined as a process of measuring the instantaneous value of an analog signal in the discrete form.

Sampling is a process performed by a sampler. It is present in almost every type of digital communication system that helps in converting an analog signal to the digital signal. An analog signal is a continuous time-varying signal, while digital signal is a signal in the discrete form. The function of a sampler is to measure the samples of the instantaneous value of the continuous signal and convert it into the discrete values.

The combination of quantizer and sampler in digital communications works as an A/D (Analog to Digital) converter. It converts an incoming analog signal to the digital signal. The sampler converts the analog signal to the discrete values and the quantizer represent each level to the fixed discrete finite set of values. Thus, we can define the analog to digital conversion as a two step process. The first step is performed by the sampler and the second step is performed by the quantizer.

The waveforms of a continuous analog signal and digital signal are shown below: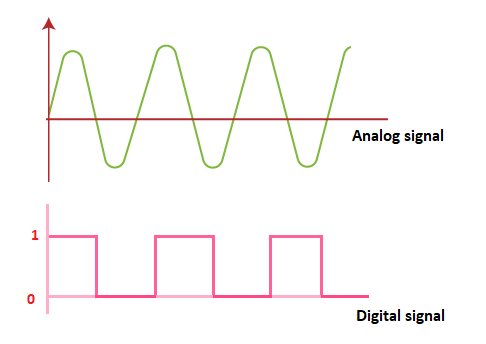

When the continuous signal is sampled at regular intervals and multiplied by a periodic pulse train, the produced signal is the sampled signal, as shown below: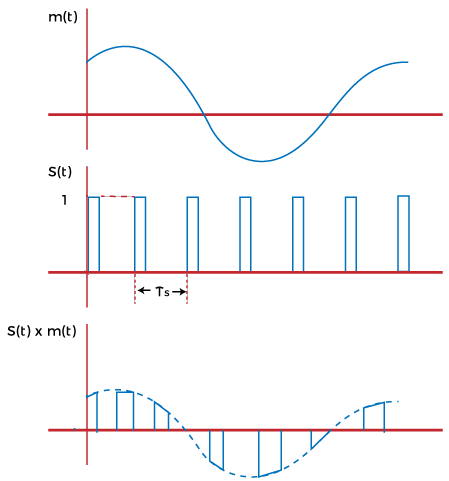

Here, we will discuss the sampling theorem, sampling rate, Nyquist rate, methods of sampling, anti-aliasing filter, advantages of sampling, disadvantages of sampling, and applications of sampling.

Sampling theorem

Sampling theorem is based on the fixed sampling rate, called Nyquist rate. Hence, sampling theorem is also known as Nyquist theorem. It is based on the theory of the bandlimited signals.

Let's discuss the sampling theorem of the bandpass signals and baseband signals.

According to the sampling theory of the bandpass signals, a signal can be successfully reconstructed if its sampling rate is not greater than the maximum frequency W. The samples are spaced at sampling time 'Ts' seconds apart without zero mean square error.

Ts = 1/2W

According to the sampling theory of the baseband signals, a signal can be successfully reconstructed if the samples are separated with a uniform intervals less than or equal to 1/2F_m.

It can be represented as:

Ts ≤ 1/2F_m

Sampling rate

Sampling rate is defined as the number of samples taken per second from a continuous signal for a finite set of values. We can also define it as a sampling frequency, which is the reciprocal of the sampling time.

Fs = 1/Ts

Where,

Fs is the sampling frequency

Ts is the sampling time

As discussed, sampling rate is an essential period for the sampler to perform sampling process. It helps in the successful recovery of the digital signal at the receiving end. Hence, a fixed parameter was defined for the sampling rate, known as Nyquist rate.

Nyquist rate

Suppose H is the highest selected frequency. A bandlimited signal is transmitted at the frequency components lower than W Hz. Thus, for the replication of the original signal, the sampling rate should be twice the highest frequency.

It is given by:

F_s = 2W

Where,

F_s is the sampling rate

W is the highest frequency

Such rate of sampling is known as Nyquist rate. The sampling at the Nyquist rate does not introduce any distortion.

Nyquist rate is also known as the minimum sampling rate and is represented by the condition:

Fs = 2Fm

Where,

Fs is the sampling frequency or sampling rate

Fm is the maximum frequency of the input signal or the message signal

Nyquist Interval

Nyquist interval is the reciprocal of the Nyquist rate. It is given by:

T_S = 1/2W

Where,

T_S is the Nyquist Interval

W is the highest frequency

Methods of sampling

The methods of sampling are classified as follows:

Ideal Sampling
Natural Sampling
Flat-top sampling

Ideal Sampling

Ideal sampling is also known as instantaneous sampling or impulse sampling. The sampling process multiplies the input signal and the carrier signal, which is present in the form of train of pulses.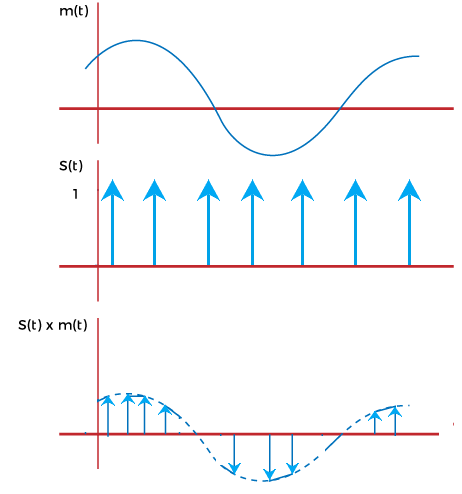

The above diagram shows the waveforms of the message signal, sampling signal in the form of train of pulses, and the sampled signal. The working principle that multiples the input signal and the sampling signal is known as multiplication principle.

Natural Sampling

Natural Sampling is considered an efficient multiplexing method in Pulse Amplitude Modulation. Here, the analog signal is multiplied by the uniformly spaced rectangular pulses.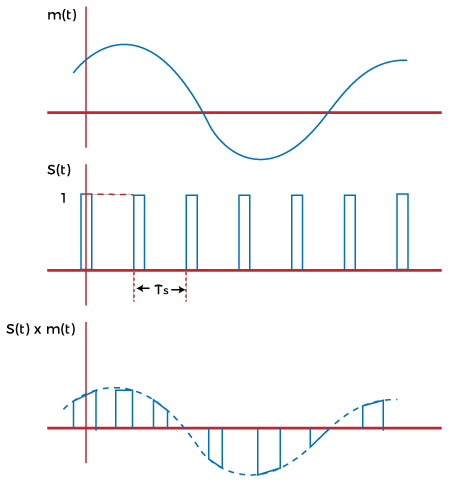

The above diagram shows the waveforms of the message signal, sampling signal, and the sampled signal.

Flat-top sampling

The design and reconstruction of flat-top sampling is easy than the natural sampling process. The pulses in the flat-top sampling method are in the flat shape at the top and are held at a constant height. It means that the samples are flat and have constant amplitude.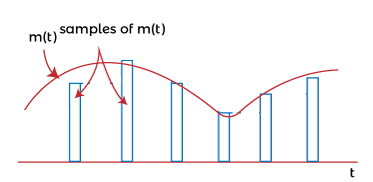

Anti-aliasing filter

Aliasing is the common effect that can arise post the sampling process. In the aliasing process, the high frequency components in the signal override the low frequency components. The aliasing occurs when the signal frequency exceeds half the sampling frequency (F_s/2).

It can be represented as:

Fm > Fs/2

2Fm > Fs

Where,

Fs is the sampling frequency or sampling rate

Fm is the maximum frequency of the input signal or the message signal

Similarly, the aliasing effect can be reduced when the sampling frequency exceeds twice the signal's frequency.

It is represented as:

Fs > 2Fm

The anti-aliasing filters are used to prevent the aliasing effect during the transmission process. The cut-off frequency of such filters is equal to half the sampling rate (F_s/2). The function of aliasing filters is to remove and filter the high-frequency components from the signal. It is inserted before the sampler. It is also known as low-pass anti-aliasing filter. The signal after passing through the anti-aliasing filter is sampled at a rate higher than the Nyquist rate. It helps in the easy recovery of the signal.

Why sampling is required?

We know that the sampling process helps in the conversion of an analog signal to the digital signal. The data transmission in the form of digital signal offers various advantages, such as high efficiency, fast speed, low cost, low interference, low distortion, and high security. Hence, sampling is essential to improve the quality and transmission ability of the signals over the communication channel.

Advantages of sampling

The major advantages of the sampling process are due to the conversion of the transmission to the digital form, which has various advantages as discussed above. It converts an analog signal to the discrete values.

The advantages of sampling are as follows:

Low cost
High accuracy
Easy to implement
Less time consuming
Low signal loss
High scope

It prevents the signal loss or any information loss by converting the incoming data to the suitable rate for transmission. For example, if a signal contains high frequency components, the sampling process will convert it into high rates for effective transmission. Generally, the input signal is sampled at the frequency rate twice that the incoming signal. It is done to preserve the full information in the signal.

Applications of sampling

Sampling describes the number of possible digital values that are used to represent a sample. Sampling is essential because it prevents any information loss during the transmission loss. It also increases the accuracy of the system. Sampling is used in various processes, such as PAM, PCM, and TDM. Let's discuss the applications of sampling in detail.

PAM (Pulse Amplitude Modulation)

In Pulse Amplitude Modulation, the amplitude of the pulse is varied with the sample value of the message signal. Pulse modulation techniques are widely used in digital transmission, where non-baseband applications are replaced by PPM (Pulse Position Modulation). PAM modulation technique is used in various applications, such as Ethernet, television, and LED lighting.

PCM (Pulse Code Modulation)

Sampler is an essential part of the PCM communication system that converts an analog signal to the digital encoded signal represented in the form of binary digits 0 and 1. It is used with the quantizer, which together works as an Analog to Digital converter. PCM is used in telephone network to convert the analog signal in the form of audio signal to the digital signal, which is the preferred signal for efficient transmission over long distances. The digital signal at the receiving end is converted back to the audio signal that appears as the same audio signal at the output.

TDM (Time Division Multiplexing)

In TDM, various signals are sampled at the same rate with the same frequency, but different time. Multiplexing is the method to transmit multiple signals on the same communication channel. The signals in TDM are transmitted at different time intervals to prevent any cross-talk or interference. The sampling rate is different because it depends on the bandwidth of the signal. The transmitted signals in TDM are placed in the sequence because it helps in its easy recovery at the receiving end.

Importance of Fourier Transform

Fourier transform is an important phenomenon in representing and analyzing the signals. For example, a 2-D Fourier transform analysis helps in removing the high frequency components from the signal, such as image signal. It is used in various applications, such as digital transmission, signal processing, image reconstruction, image compression, optics, and probability.

The various features and advantages of the Fourier transform are as follows: